在二十世纪第一次数学家大会上，希尔伯特提出了“完美数学问题”准则，随后他举了两个例子，一个是费马猜想，另一个就是N体问题。近现代研究最多的就是三体问题。

        三体问题就是三个天体在万有引力作用下的运动问题。三个天体的质量、初始位置和初始速度都是未知的，求解难度很大，所以一般研究的都是有条件束缚下的限制性三体问题，而平面圆型限制性三体问题（PCR3BP）是其中最为简单的一种模型。

PCR3BP问题再近现代的月球火箭理论中的到了应用，其中一种就是击中月球轨道。先来看一个简单的发射问题：

        月球背面有一空间站，现要利用一从地球发射的无动力火箭对其进行补给，求：发射速度和角度。

        这是一个经典的PCR3BP问题。其中，火箭可以视为质量无限小的质点，其对地球和月球作用力忽略不计，在整个系统中，太阳对地、月、火箭的影响可以忽略，那么仅需要考虑两个运动：月球

        由于是无动力火箭，所以我们选取高度为600km的地月转移轨道为出发点，选取出发点与地心连线和x负向的夹角为θ,在平面内延顺时针方向发射火箭，同时月球从（L，0）处开始公转，发射速度大小 为v0，月球速度大小vm，并取最终位置的误差角为发射状态是否合理的判断依据（如图-1）。

 围绕地球的公转和火箭在地球和月球引力下的运动轨迹。

图-1

      

        在MATLAB中模拟时，向量以坐标的形式表示，取积分时间 dt=0.05,通过对不同的初始位置（用角度θ表示）和发射速度下，火箭和月球最近距离的计算可以得到一系列数值解(θ，v )。由于我们设备计算能力有限，所以只计算了v=11 km/s时的发射角度。在进行一系列模拟之后，得到了一个误差角关于角度的拟合曲线，最终确定了一个比较合理的一个发射角度θ=48.53873768°(π *773168/2867200）

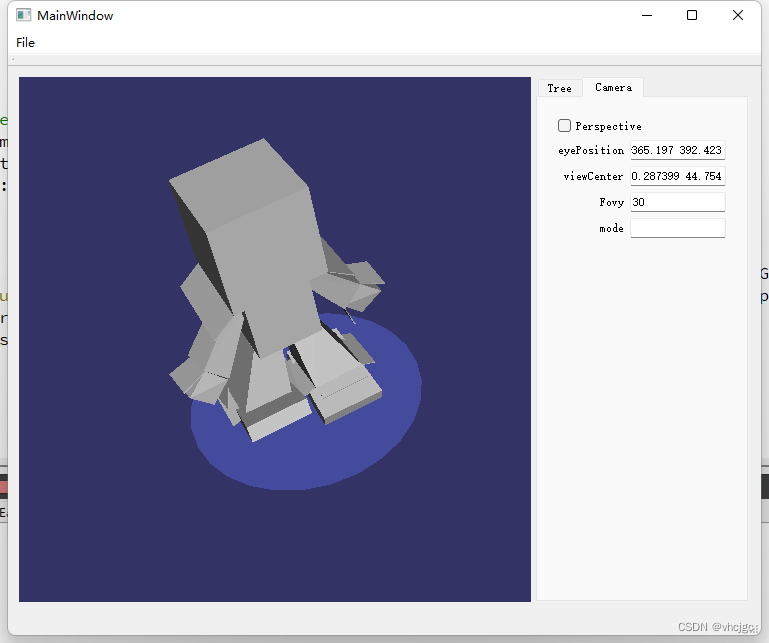
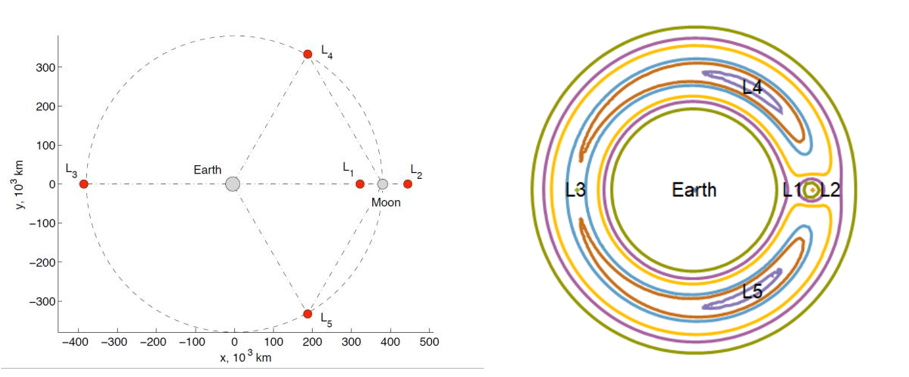
以下是拉格朗日点的绘制以及等速度曲线的绘制。

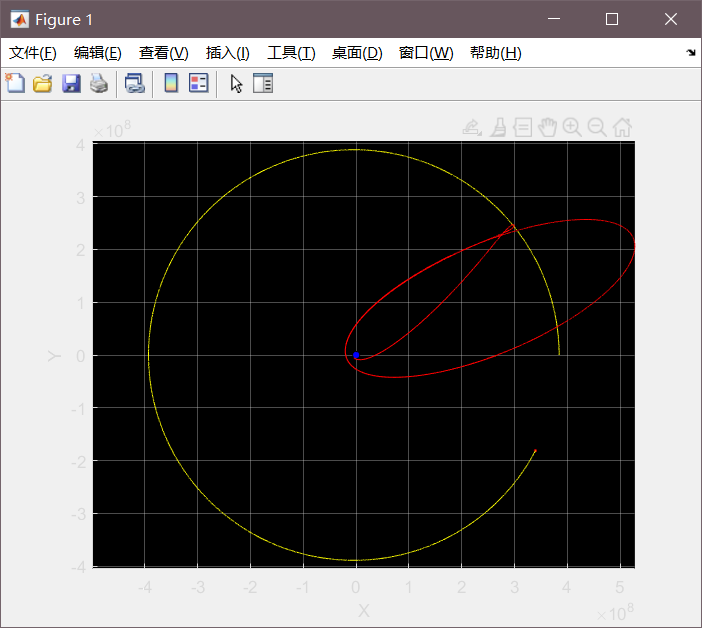
以下是没有被俘获的一种轨道（很好玩）

资料下载 🍞正在为您运送作品详情