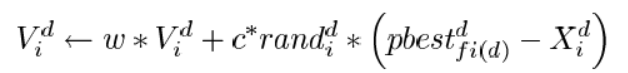粒子群算法及其改进

1 粒子群算法介绍

求解非线性最优化问题时，有一种比较常用的算法为智能体算法，这里我们介绍的粒子群算法就隶属于智能体算法。

粒子群算法是模拟鸟寻找食物：一群鸟在随机的搜索食物。在这个区域里只有一块食物，所有的鸟都不知道食物在那。但是它们知道自己当前的位置距离食物还有多远。然后他们根据群体中个体之间的协作和信息共享来寻找到食物。

2、粒子群算法介绍

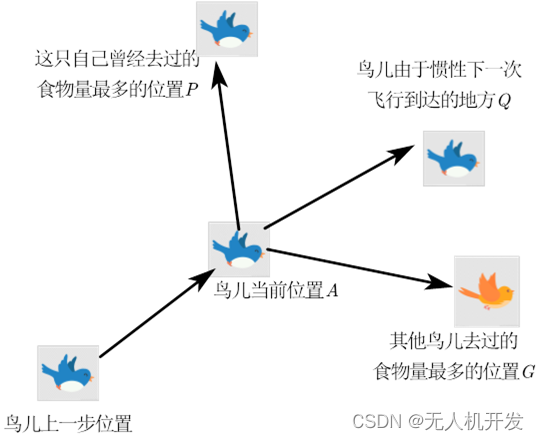在这里插入图片描述在粒子群优化算法中，每个解可用一只鸟（粒子）表示，目标函数就是鸟群所需要寻找的食物源。寻找最优解的过程中，粒子包含两种行为：个体行为和群体行为。

个体行为：粒子根据自身在寻优过程中的最优解更新自己的位置。

群体行为：粒子根据群体在寻优过程中的最优解更新自己的位置。

假设N个粒子组成1个粒子群，每个粒子都是一个D维向量，则每个粒子的位置为：

将其代入适应度函数(优化问题的目标函数）计算出适应度值，第i个粒子经历过的最优适应度值的位置记为个体历史最优：

整个粒子群经历过的最优位置记为全局最优：

在找到上述这两个最优值后，粒子通过下面的公式来更新自己的速度和位置。

根据上述公式可知，每个鸟将向着自己和种群最优的方向出发。是粒子的当前位置。和是学习因子。粒子都有一个最大限制速度Vmax，如果某一维的速度超过设定的Vmax ，那么这一维的速度就被限定为Vmax 。

3、各种粒子群算法改进

1、将学习因子自适应话； 2、引入遗传算法特性，与之进行结合； 3、结合混沌特性，使其不易陷入局部最优； 4、二阶粒子群算法 5、与模拟退火算法结合； 6、二阶振荡粒子群算法

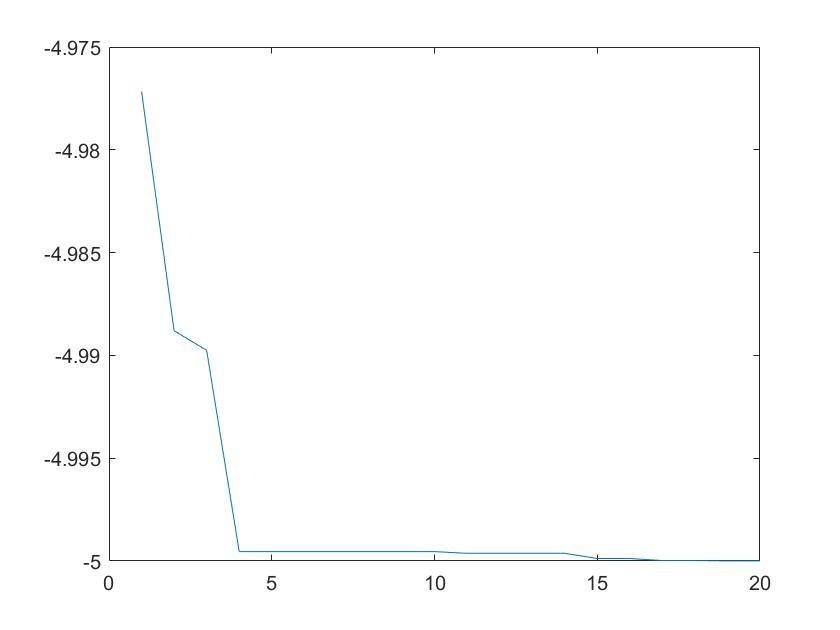
4、部分代码及仿真结果

for t=1:M
    for i=1:N
        w = wmax - (t-1)*(wmax-wmin)/(M-1);
        v(i,:)=w*v(i,:)+c1*rand*(y(i,:)-x(i,:))+c2*rand*(pg-x(i,:));
        x(i,:)=x(i,:)+v(i,:);
        if fitness(x(i,:))<p(i)
            p(i)=fitness(x(i,:));
            y(i,:)=x(i,:);
        end
        if p(i)<fitness(pg)
            pg=y(i,:);
        end
    end
    Pbest(t)=fitness(pg);
end