线性滤波/卷积

（注：这部分摘自这篇博客）
线性滤波可以说是图像处理最基本的方法，它可以允许我们对图像进行处理，产生很多不同的效果。做法很简单。首先，我们有一个二维的滤波器矩阵（有个高大上的名字叫卷积核）和一个要处理的二维图像。然后，对于图像的每一个像素点，计算它的邻域像素和滤波器矩阵的对应元素的乘积，然后加起来，作为该像素位置的值。这样就完成了滤波过程。

对图像和滤波矩阵进行逐个元素相乘再求和的操作就相当于将一个二维的函数移动到另一个二维函数的所有位置，这个操作就叫卷积或者协相关。卷积和协相关的差别是，卷积需要先对滤波矩阵进行180的翻转，但如果矩阵是对称的，那么两者就没有什么差别了。

实际应用——加密

很多我们熟知的图像处理其实都可以由由滤波和卷积简单做到。比如锐化，软化，浮雕及高斯模糊，具体效果及原理可看这篇文章
加密是社会中一项很重要的应用，也是信息传播中的一项重要安全措施。对于这个问题，本人思考了下滤波在图像加密中的应用。滤波和卷积都存在对应的逆操作，要想对图像加密的话，选定一个甚至多个卷积核对图像进行变换从而可以得到一个隐含内容的无规则图样。解密的时候需要按照对应的顺序进行对应的逆操作便能得到原图样。但是逆滤波和逆卷积涉及的知识面都比较深在下还没怎么弄懂orz。想要更深入学习的可以参考逆滤波及反卷积。
这里介绍一种在下自己思考的一种比较简单的加密算法。

二维前缀和思想

假如我们选定卷积核为中心及中心的左上区域都为1的矩阵对图像进行操作，可以想见加密图样的每个像素点都是对应位置的原图像及其左上方一定区域内的信息之和，我们称之为前缀和，需要注意的是这个前缀和不是某位置及左上部分所有信息之和而是有一定范围内的。下图展示了4*4的图像矩阵的滤波过程。

可以看到左上第一个像素点由于左上没有其他信息了，所以加密后的对应点信息就是其本身。它右边面第一个像素点加密后则有其本身和最左上像素点信息之和。减去最左上信息则可得到第二个点的原信息。依次类推，我们可以还原图像的全部信息。参考代码如下：

#include<stdio.h>
#include<algorithm>
using namespace std;
int m;//原图像大小m*m 
int s1[200][200];//原图像
int s2[200][200]={	{0,1,3,5},{4,10,14,18},{12,26,30,34},{20,42,46,50}};//加密图像 
int n;//卷积核大小n*n
int r;//卷积核半径 
int c[200][200]={	{1,1,0},{1,1,0},{0,0,0}};//convolution kernel 卷积核 
void read()
{scanf("%d",&m);for(int i=0;i<m;i++){for(int j=0;j<m;j++){scanf("%d",&s2[i][j]);}}
}
void read_kernel()
{scanf("%d",&n);r=(n+1)/2;//默认卷积核边长为奇数 for(int i=0;i<r;i++){for(int j=0;j<r;j++){c[i][j]=1;}}
}
int main()
{//read();//read_kernel();m=4;n=3; r=2;for(int i=0;i<m;i++){for(int j=0;j<m;j++){s1[i][j]=s2[i][j];for(int x=max(i-r+1,0);x<=i;x++){for(int y=max(j-r+1,0);y<=j;y++){if(x==i&&y==j) continue;s1[i][j]-=s1[x][y];}}}}for(int i=0;i<m;i++){for(int j=0;j<m;j++){printf("%d\t",s1[i][j]);}printf("\n");}return 0;
}

这份代码的时间复杂度为O(m²r²)的，其实还有很多可优化的地方，有兴趣可以自行优化一下。

更复杂的卷积核——更好的加密效果

形如上述所说的卷积核会使一部分的信息直接相加，其实在实际中加密效果可能并不理想，甚至还是可以看得出原图像的大致内容。所以我们考虑将卷积核中的参数变化来使变换更无规则可循。如果理解了上述代码，其实可以发现前缀和这个性质其实没有得到太大的利用。每次还原（i，j）像素点的时候，其左上所有像素点都已成功还原，而我们则是用对应加密信息一个个减去左上像素点的原本信息来还原该像素点原本信息。如果这个卷积核的左上部分不是1，是不是也能用同样的方法来消除其他点对待处理像素点信息的影响呢。其实我们可以把卷积核中的数值视作权值，再用待处理像素点加密信息来加上其他点乘以对应权值的相反数，最后再乘上它本身对应权值的倒数就可以得到其原本信息了。

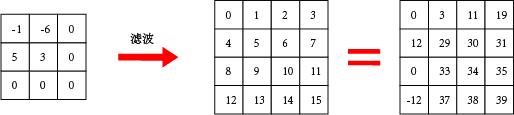
参考代码如下

#include<stdio.h>
#include<iostream>
#include<time.h> 
#include<algorithm>
using namespace std;
int m;//原图像大小m*m 
int s1[200][200];//原图像
int s2[200][200]={	{0,3,11,19},{12,29,30,31},{0,33,34,35},{-12,37,38,39}};//加密图像 
int n;//卷积核大小n*n
int r;//卷积核半径 
int c[200][200]={	{-1,-6,0},{5,3,0},{0,0,0}};//convolution kernel 卷积核 
void read()
{scanf("%d",&m);for(int i=0;i<m;i++){for(int j=0;j<m;j++){scanf("%d",&s2[i][j]);}}
}
void read_kernel()
{scanf("%d",&n);r=(n+1)/2;//默认卷积核边长为奇数 for(int i=0;i<r;i++){for(int j=0;j<r;j++){c[i][j]=1;}}
}
int main()
{//read();//read_kernel();m=4;n=3; r=2;for(int i=0;i<m;i++){for(int j=0;j<m;j++){s1[i][j]=s2[i][j];for(int x=0;x<r;x++){for(int y=0;y<r;y++){if(i-r+1+x<0||j-r+1+y<0) continue;if(x==r-1&&y==r-1) continue;s1[i][j]-=c[x][y]*s1[i-r+1+x][j-r+1+y];}}if(c[r-1][r-1]!=0) s1[i][j]/=c[r-1][r-1]; }}for(int i=0;i<m;i++){for(int j=0;j<m;j++){printf("%d\t",s1[i][j]);}printf("\n");}return 0;
}

补充

可以观察到其实卷积核中非零部分不一定要在左上，在另外三个方向也是没有关系的。我们也可以用多种不同的卷积核对图像进行多方向多重加密使加密效果更加优秀。解码时也仅需反过来按顺序进行多次逆运算就能还原图像了。

参考资料

[1]https://blog.csdn.net/zouxy09/article/details/49080029
[2]https://blog.csdn.net/haoji007/article/details/53911940
[3]https://blog.csdn.net/qq_16234613/article/details/79387345)
[4]https://blog.csdn.net/mmmmmk_/article/details/82942783
[5]https://baike.baidu.com/item/图像处理/294902?fr=aladdin#2