最近学习了ORB_SLAM2中计算sim3变换，其中对什么是尺寸因子和尺寸漂移问题还存在一些知识盲区，因此查看了一些别人写的文章以及自己的理解整理了一下这个问题。（感觉自己的理解还不是非常的准确，如果有朋友发现我理解不对的地方，欢迎在评论区指出，十分感谢！）

1.在理解这个问题之前先明白什么是尺度一致性（尺度不变性）？

以下面三张图为例（别人文章截取）：

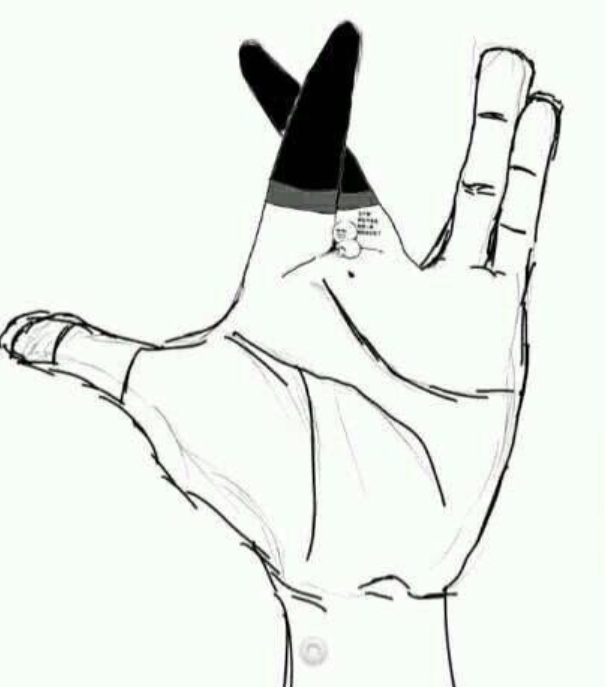
上面三张图像可以看作是相机由近到远依次拍摄，假如图片中小人的真实身高有1.8m，表现在图像里的话，图一小人占比50%的像素，图二小人占比5%像素，图三小人占比1%像素。如果按照所占像素的多少来确定一个物体大小的话，这个小人在三个图像中的大小就不一样了，但是小人的真实大小就是身高1.8m，因此不能依据一个物体所占像素的多少来确定一个物体大小。

所以为了实现尺度不变性（即使用一个标准可以表示三张图像中的小人大小一样），需要给特征加上尺度因子。在进行特征描述的时候，将尺度统一就可以实现尺度不变性了。

在slam里面我对尺度因子的理解是深度信息，如果我能知道这三张图像中的小人的深度信息的话，我就能通过小人所占像素多少+小人的深度作为标准来衡量图片中一个物体的真实大小了，这就实现了尺度不变性。

例如：第一张图片中小人占500个像素，计算得到深度为2,计算标准为500*2=1000；

第二张图片中小人占50个像素，计算得到深度为20,计算标准为50*20=1000；

第三张图片中小人占10个像素，计算得到深度为100,计算标准为10*100=1000；

所以最后经过这个标准将尺度统一后，三张图片中小人的尺度都为1000，实现了尺度不变性。

2.单目视觉slam中尺寸漂移问题

我的理解是保证尺度一致性的前提是计算出来的深度信息和距离信息是准确的。

单目视觉slam中尺寸漂移问题根本原因是单目相机无法仅根据一张图片得出物体的真实大小，也就无法确定物体的远近（深度距离），同理无法得出运动的尺度大小（运动距离），这是产生尺度漂移的根源。

同时，在使用三角测量原理计算深度时，受到特征点匹配精度的影响，较小的角度误差在经过多帧累积之后深度误差都会变得很大，从而无法保证尺度一致性。

在单目初始化的时候，先提取关键点并匹配，再根据对极几何求本质矩阵E，再从E中恢复R,t。其中得到的t是个单位向量，因为任意缩放t，极线约束都成立。你可以对t进行任意缩放。缩放完后，设第0帧的位置为相机坐标系原点，则第1帧的位置就可以由R, t得到。虽然这个t不是真值，但是可以固定下来。然后根据两帧的位置，可以对图像帧0和1中匹配的三维点进行三角化。（多点获取本质矩阵；恢复R,t；并根据R,t三角化计算出伪深度 ）。

在单目初始化之后对于新的图像帧，都是通过前一帧的R，t为基础来计算当前帧的R,t，再利用该R,t三角化出地图点。问题就是，由于受到特征点匹配精度的影响，如果第一步算的R,t有误差，那么第二步三角化的三维点的深度就存在误差，也就是说其深度会存在一个缩放。对于新来的每一帧，都会有这样的问题，经过多帧累积之后深度误差都会变得很大，从而无法保证尺度一致性。

3.解决办法：

1、视觉和IMU融合。IMU可以测得高帧率的角速度和加速度，尤其当相机运动过快时，相机会出现运动模糊，或者两帧之间重叠区域太少以至于无法进行特征匹配，所以IMU是视觉信息的很好的补充，能在相机运动过快的时候给出一个较好的位姿估计。

2、后端优化时把尺度也作为一个优化变量，也可以减小尺度漂移问题。

4.为什么双目和深度相机没有尺寸漂移问题

由于相机结构的原因，双目相机和深度相机计算出来的深度信息和距离信息是准确的，因此不存在尺度漂移问题。

参考文章：

1.https://blog.csdn.net/qq_16184125/article/details/115053997

2.https://blog.csdn.net/lv15076050705/article/details/123644797?ops_request_misc=&request_id=&biz_id=102&utm_term=%E4%BB%80%E4%B9%88%E6%98%AF%E5%8D%95%E7%9B%AE%E7%9A%84%E5%B0%BA%E5%BA%A6%E6%BC%82%E7%A7%BB&utm_medium=distribute.pc_search_result.none-task-blog-2~all~sobaiduweb~default-2-123644797.142^v74^insert_down1,201^v4^add_ask,239^v2^insert_chatgpt&spm=1018.2226.3001.4187