数据关联分析用于挖掘数据对象之间的关系,例如啤酒和尿布的案例

一.基本概念

通过实例认识项集,支持度,频繁项集,关联规则,置信度,强关联规则,支持度,置信度

• 运动器的历史购买数据

TID	网球拍	网球	运动鞋	羽毛球
1	1	1	1	0
2	1	1	0	0
3	1	0	0	0
4	1	0	1	0
5	0	1	1	1
6	1	1	0	0

• TID: 表示每一次购物单的序号
• 0和1: 表示是否在本购物单中存在该商品

符号设置:

• D: 交易数据库,实例中的表格
• T: 每次交易事务,实例中一列的购买数据
• I: 项的集和{I₁，I₂,…,I_n}

1.项集概念

项集: 在集和中,包含k个项的集和称为k项集

• 实例如下

TID	集和	项集
1	{网球拍,网球,运动鞋}	3项集
2	{网球拍,网球}	2项集
3	{网球拍,}	1项集
4	{网球拍,运动鞋}	2项集
5	{网球,运动鞋,羽毛球}	3项集
6	{网球拍,网球}	2项集

2.关联规则

A=网球拍，B=网球
$$p(A=>B)=p(AB)=\frac{count(AUB)}{|D|}$$

3.支持度和置信度概念

支持度: 表示数据集D中出现项集A的概率
$$公式:support(A\subseteq T)=\frac{count(Abaohan)}{|D|}$$
置信度: 表示关联规则前价出现时后价查询的概率。
$$support(A=>B)=\frac{count(A\cup B)}{|D|}$$

• 实例如下
  探究网球拍和网球的支持度
  设x=买网球拍事务集,y=买网球事务集求p(x=>y)=p(xy)
  x=5,y=4,x∪y=3,D=6
  $$支持度:\frac{x\cup y}{|D|}=3/6=0.5$$
  $$置信度:\frac{x\cup y}{x}=3/5=0.6$$

4.频繁项集

自行数组阈值,若支持度>=阈值就是频繁项集
设阈值为=0.4
p(网球拍=》网球)支持度=0.5 是频繁
p(网球拍=》运动鞋)支持度=0.33 不是频繁

5.超项集

S₁={ABC} ,S₂={ABC？} ,？: 量子叠加态

• S₁中所有元素在S₂中存在
• S₂可能包含S₁中没有的元素

S₂是S₁的超项集
S₁是S₂的子集

6.闭频繁集

？: 量子叠加态

S1	BC
S2	ABCD
S3	BCD
S4	AD

S₂是S₁的超项集
S₁支持度=3/4
S₂支持度=1/4
S₁!=S₂则S₁是闭项集
若S₁>阈值S₁是闭频繁集

7.极大频繁集

S1	BC
S2	ABCD
S3	BCD
S4	AD

阈值=0.6

• S₁的所有真超项集:S₂,S₃。
• S₁是频繁项集,S₂不是频繁项集S₃不是频繁项集
• S₁是极大频繁项集。声明S₁项集进一步扩展就不是频繁项集
  $$S_1\subseteq S_1所有的真超项集，S_1是频繁项集,S_1所有的真超项集不是频繁项集,S_1是极大频繁项集$$

8.反单调性

若项集A是频繁项集,则其所有子集为频繁项
若项集A不是频繁项集,则A所有超项集为不频繁项集

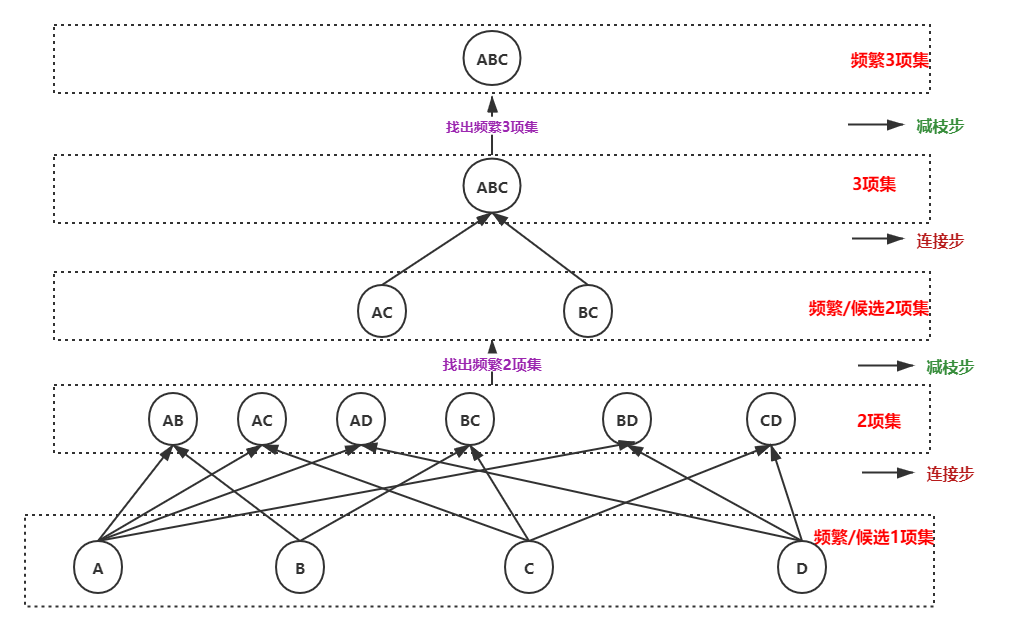
9.APriori算法

• 连接步:
• 减枝步:

示例

S1	ABC
S2	BCD
S3	CE
S4	ABC

阈值=0.3

N项集	N=1	N=2	N=3
频繁项集	{A}{B}{C}{D}	{AC}{BC}	{ABC}