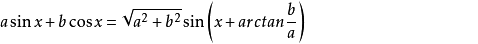求导及求微分的基本公式:

泰勒中值定理:


麦克劳林公式:

不定积分公式:

凑微分:
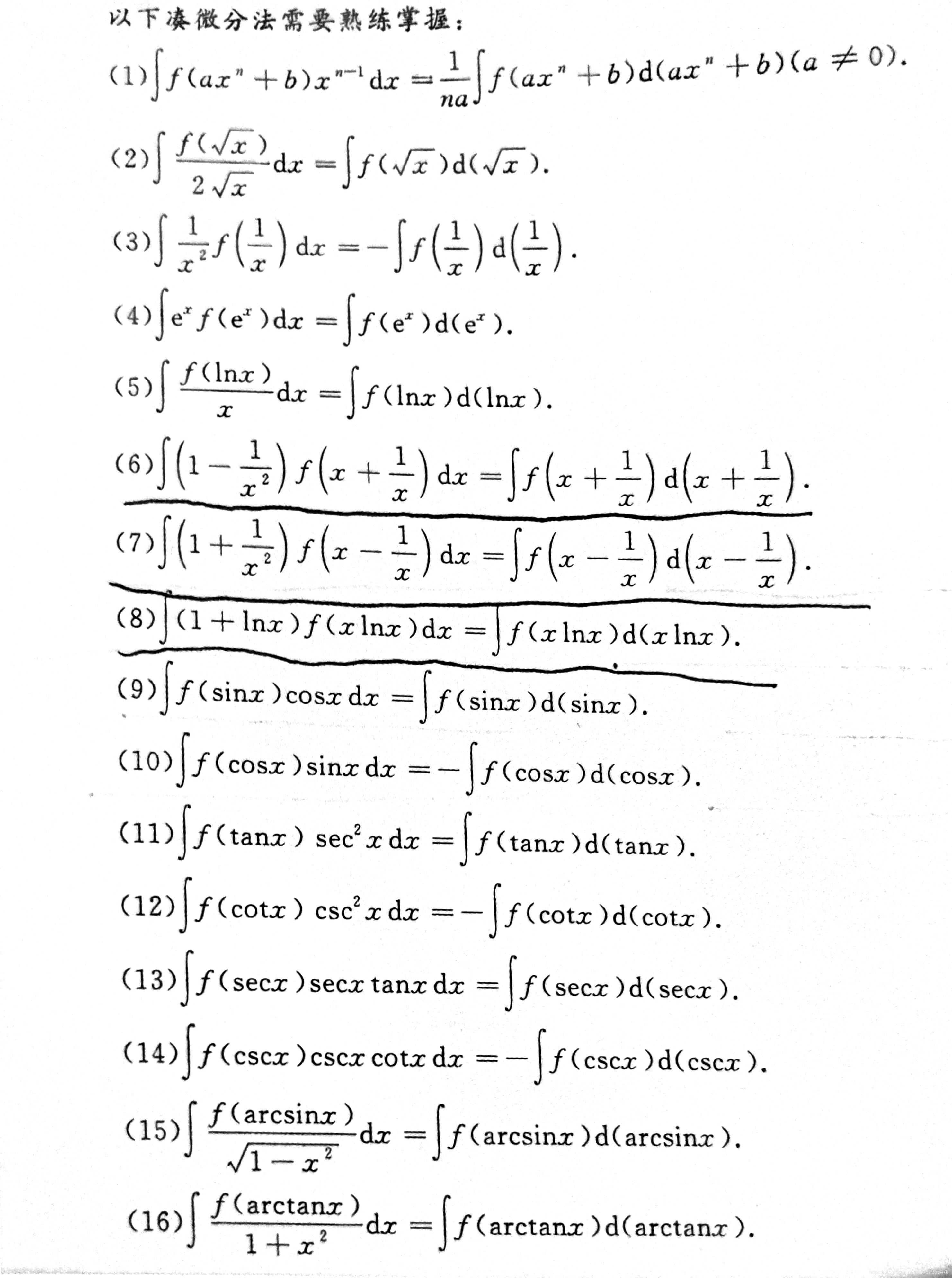
第二类换元积分法常用的三种情况:

求高阶导数的几个公式:
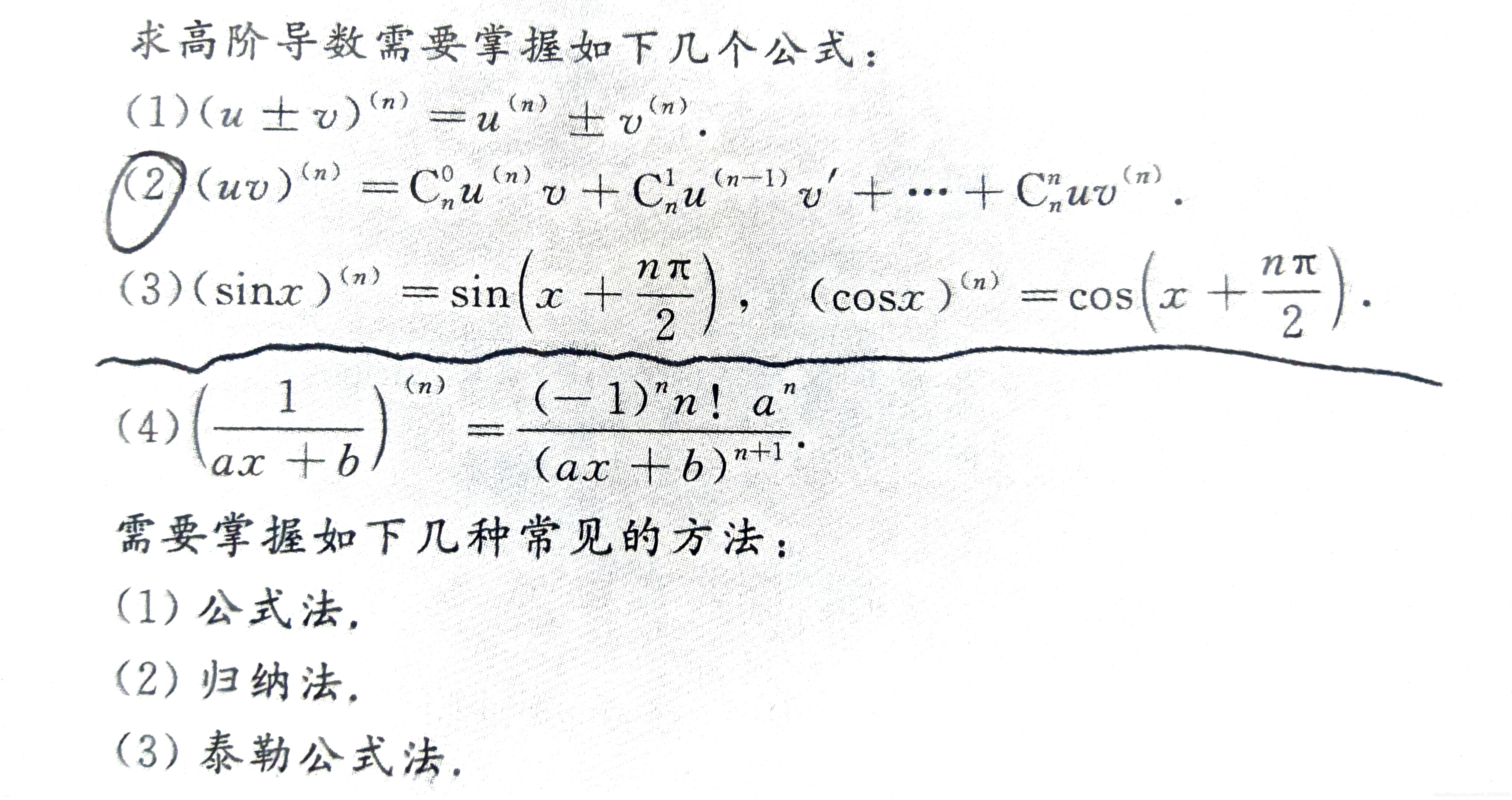
二阶常系数非齐次线性微分方程的特解:

排列组合公式:
C的计算:
下标的数字乘以上标的数字的个数,且每个数字都要-1.再除以上标的阶乘.如:C5 3(下标是5,上标是3)=(5X4X3)/3X2X1.
3X2X1(也就是3的阶乘)
A的计算:
跟C的第一步一样.就是不用除以上标的阶乘.
如:A4 2 = 4X3 .
诱导公式:
公式一:
设α为任意角,终边相同的角的同一三角函数的值相等:
sin(2kπ+α)=sinα (k∈Z)
cos(2kπ+α)=cosα (k∈Z)
tan(2kπ+α)=tanα (k∈Z)
cot(2kπ+α)=cotα (k∈Z)
公式二:
设α为任意角,π+α的三角函数值与α的三角函数值之间的关系:
sin(π+α)=-sinα
cos(π+α)=-cosα
tan(π+α)=tanα
cot(π+α)=cotα
公式三:
任意角α与 -α的三角函数值之间的关系:
sin(-α)=-sinα
cos(-α)=cosα
tan(-α)=-tanα
cot(-α)=-cotα
公式四:
利用公式二和公式三可以得到π-α与α的三角函数值之间的关系:
sin(π-α)=sinα
cos(π-α)=-cosα
tan(π-α)=-tanα
cot(π-α)=-cotα
公式五:
利用公式一和公式三可以得到2π-α与α的三角函数值之间的关系:
sin(2π-α)=-sinα
cos(2π-α)=cosα
tan(2π-α)=-tanα
cot(2π-α)=-cotα
公式六:
π/2±α及3π/2±α与α的三角函数值之间的关系:
sin(π/2+α)=cosα
cos(π/2+α)=-sinα
tan(π/2+α)=-cotα
cot(π/2+α)=-tanα
sin(π/2-α)=cosα
cos(π/2-α)=sinα
tan(π/2-α)=cotα
cot(π/2-α)=tanα
sin(3π/2+α)=-cosα
cos(3π/2+α)=sinα
tan(3π/2+α)=-cotα
cot(3π/2+α)=-tanα
sin(3π/2-α)=-cosα
cos(3π/2-α)=-sinα
tan(3π/2-α)=cotα
cot(3π/2-α)=tanα
(以上k∈Z)
数集
有理数,整数和分数的统称,一切有理数都可以化成分数的形式。
实数,有理数和无理数的统称。
无理数,无限不循环的数。
自然数,全体非负整数。
正整数指的是1,2,3,4,5……那类的数
自然数包括0和正整数。
整数包括负整数,0,正整数。
整数就是指…… -3 -2 -1 0 1 2 3 ……那类的数。不是自然数的整数是负整数,指-1 -2 -3……那类的数。
有理数就是能写成两整数之比的数。有理数包括整数和分数,分数就是指不是整数的有理数,所有有限小数和无限循环小数都是分数。
实数是有理数和无理数的统称。无理数就是无限不循环小数,不能写成两个整数之比的实数,所有的小数和整数都是实数。
实数={有理数}∪{无理数}
还有复数。复数指a+bi(a,b为实数,其中i^2=-1)形式的数。复数就是实数和虚数的统称。其中b=0时该复数为实数,其他的都是虚数,a=0,b≠0时为纯虚数。
还有超实数,就是实数集中扩展无穷大和无穷小数的数集。
自然数:N,正整数:N+,整数:Z,有理数:Q,实数:R,复数:C。
其中自然数,正整数,整数,有理数都是可数集,实数和复数是不可数集。
可数集就是能够和自然数一一对应的无限集合,不可数集就是不能与自然数集一一对应的无限集合。自然数的位数都是有限的,而实数的小数部分是无限的,所以潜无限还是实无限穷竭,实数都是不可数的。有理数,写成p/q,列表格,对角线排列就可以证明有理数可数。
一图胜千言:
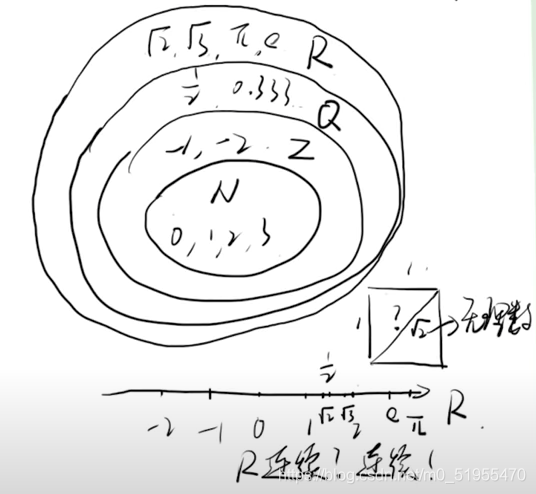
实数集R是连续的,这也是微积分的基础。
辅助角公式: