作者丨小马
编辑丨极市平台
写在前面
目前正常卷积的感受野大多都是一个矩形的,因为矩形更有利于储存和计算数据的方便。但是,人类视觉系统的感受野更像是一个圆形的。因此,作者就提出,能不能将CNN卷积核的感受野也变成圆形呢?作者通过一系列实验,发现了圆形的卷积核确实比方形的卷积效果会更好。基于此,作者在本文中提出了一种卷积核大小可变的并且聚合了方形和圆形特点的集成卷积核。作者在模型训练结束后,采用了一种重参数的方法对模型的结构和参数进行修改,使得模型在inference的时候并没有引入额外的参数量和计算量。最终作者在分类任务的三个数据集ImageNet、CIFAR-10、CIFAR-100上进行了测试,发现了新的卷积核能够有比较大的性能提升(在MobileNetV3-Small上提高了5.20%的top-1准确率,在MobileNetV3-Large上提高了2.16%的top-1准确率)。
刚刚搜索了一下人的视野范围是什么形状的。发现其实人眼的感受野也不是圆形的,而是一个椭圆形的。类似下面的这样:


(图片来自学习强国app慕课中的“高维看世界”)
好奇之后会不会有工作进行了提出一个椭圆形的卷积核。除此之外,人眼的感知除了“上下左右”,还有“前后”。之后会不会有人提出一个带深度的卷积核(比如椭球形状的卷积核)。目前的卷积在通道维度上都是进行非常充分的建模,导致在通道维度上的建模很多时候是冗余的(这一点Involution[1]中也有提到),所以说不定用一个带“深度”信息的卷积核,只对相邻通道信息进行建模,反而能够提升模型的泛化能力。
1. 论文和代码地址
Integrating Circle Kernels into Convolutional Neural Networks
论文地址:https://arxiv.org/abs/2107.02451
代码地址:未开源
2. Motivation
从LeNet开始,矩形的卷积核一直都是CNN的标配。在这期间也有一些工作研究了可变形的卷积,但是,虽然可变形的卷积能够提高模型的performance,但是不可避免的引入了额外的参数和计算量。
因此,受人眼视觉系统感受野的启发,作者就想能不能提出一个圆形的卷积操作,相比于矩形的卷积,圆形的卷积核主要有以下几个优点:
1) 圆形卷积核的感受野和生物视觉的感受野更加相似;
2) 卷积核的感受野通常应该是各个方向都是对称的,这样可以适应全局或者局部输入特征在不同方向上的信息变化,圆形卷积核具备这个性质,但是矩形卷积核只在固定的几个方向是对称的;
3)之前也有工作表明,矩形卷积核的有效感受野更加接近圆形的高斯分布,因此,为什么不直接用一个圆形的卷积核呢?
在构造圆形卷积核时,由于感受野上的一些点通常不在网格上,因此作者采用双线性插值进行逼近,并提取了相应的变换矩阵。
最终,作者并没有采用了单独的圆形卷积,而是采用一种圆形和方形集成的卷积,并在训练过程中采用自适应的卷积核大小(也就是说,每个集成的卷积核都有一对方核和圆核。这两个核共享权值矩阵,但有不同的变换矩阵 )。
最终作者在分类任务的三个数据集ImageNet,CIFAR-10,CIFAR-100上做了实验,在不同baseline结构上,方形和圆形集成的卷积核相比于baseline都有明显的性能提升。
3. 方法
3.1. 圆形卷积核 VS 方形卷积核

圆形卷积核(b)和方形卷积核(a)如上图所示
对于一个3x3的方形卷积,可以用下面的公式表示(对感受野内的特征进行加权求和):
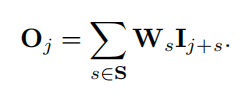

对于半径为1的圆形卷积,可以被建模成下面的公式:


由于圆核的接受场包含不是整数的位置,所以作者使用了双线性插值获取相应的采样值:

因此,将上面的两个公式进行结合,我们就可以得到下面统一的圆形卷积核的公式:

(注意,这里的圆形的卷积核的公式看上去比较复杂,但其实由于乘法的结合律,这里的矩阵 W W W和 B B B其实是可以合成一个新的矩阵的,所以在测试的时候其实并不会引入新的计算量和参数量)
(另外,再通俗的解释一下,这里的圆形卷积计算其实方形卷积计算是一样的,都是对感受野内特征信息进行加权求和;不同的是,方形的卷积核的特征信息都可以轻松的获得,但是圆形感受野内的信息由于位置往往不是整数,所以需要用双线性插值的方法,计算相应位置的特征值)
3.2. 集成圆形卷积核和方形卷积核
在本文中,作者并没有单独的使用圆形或者方形的卷积,而是对这两个卷积进行了集成。
每个集成的卷积核都有两种感受野(圆形和方形)。训练时,每层的所有卷积核都随机选择的圆形或者方形的卷积核进行训练。所以,一个集成核的感受野是一个伯努利随机变量 E ∼ B e r ( S , R ; 0.5 ) E ∼ Ber(S, R; 0.5) E∼Ber(S,R;0.5),集成核的输出卷积结构可以被表示成:

由于每一层都有两种卷积方式,并且在训练的时候,每一层的卷积都会随机选择这两种卷积中的任意一种,所以对于L层,就有 2 L 2^L 2L中不同的子网络结构。(这一步随机选择也是大大提高了模型的学习空间 )
3.3. 可学习大小的卷积核

不同感受野大小的圆形和方形卷积核如上图所示。在训练时,作者采用了一个可学习的参数 a a a动态控制了卷积核感受野的大小。
方形卷积核的感受野为 D s = a S D_s=aS Ds=aS,圆形卷积核的感受野为 D c = a R D_c=aR Dc=aR。由于在训练过程中,卷积核的形状是随机选择的,所以训练过程的感受野大小也符合伯努利分布 D c = a R D_c=aR Dc=aR。
3.4. 测试时重参数
卷积的过程可以用下面的公式表示:

上面也提到了 B B B在训练完成后其实是一个固定的矩阵,由于乘法的结合律,其实是可以将 B B B矩阵的参数和 W W W的参数进行合并(类似两个FC变成一个FC)。可以在推理之前保存由转换矩阵重参数后的新权重,模型就不再需要根据测试的偏移量逐点进行特征映射。
3.5. Integrated Kernels
对于一个正常的卷积,他的所有参数都是静态,可以被表示成:

带有自适应参数的卷积可以被表示成:

其中$ \hat{\theta}$表示动态自适应的参数。

本文的训练的网络结构如上图所示,本文模型的输出结果可以被表示成:

其中 M u l ( ) Mul() Mul()是一个多重伯努利分布,因为每一层的卷积过程都是随机的,每一层随机从N中卷积方式里选择一种,对于L层,就有 N L N^L NL种不同的组合方式。
4.实验
4.1. Circle Kernels VS Square Kernels

如上图所示,感受野越大,圆形卷积的感受野就更像一个圆形

如上表所示,作者在WRNCifar和DenseNetCifar上做了实验。随着卷积核大小的增加,圆核比方核的优势变得更加显著,表明了圆核的优越性。
4.2. Comparison on CIFAR Datasets
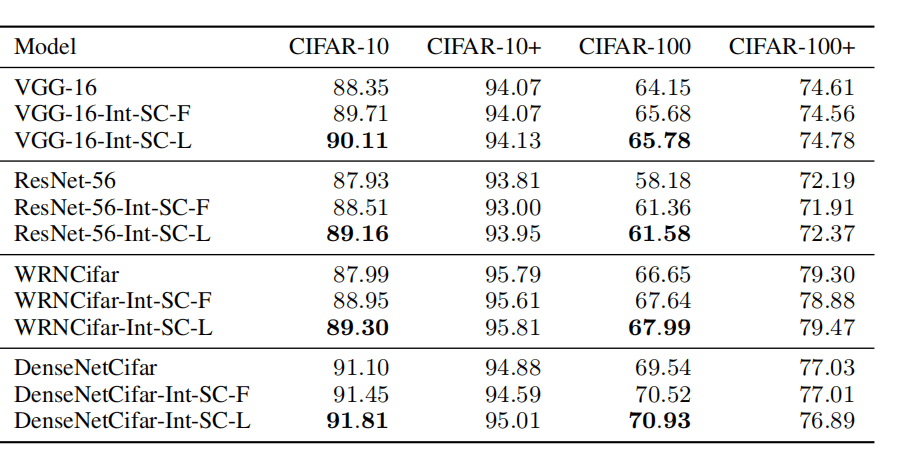
XXX-Int-SC-F表示具有固定大小的方形和圆核,XXX-Int-SC-L表示具有可学习大小的方形和圆核。
可以看出,在没有数据增强的情况下,方核和圆核的方法相较于baseline都有性能的提升,并且可学习大小的集成核在性能上表现最好。
4.3. Comparison on ImageNet

在ImageNet上,作者基于MobileNet和ResNet进行了实验。可以看出,圆核的方法会比方核的性能要更好。总体来说,可以学习的圆核和方核在性能上表现会更好一些。
4.4. Ablation Studies
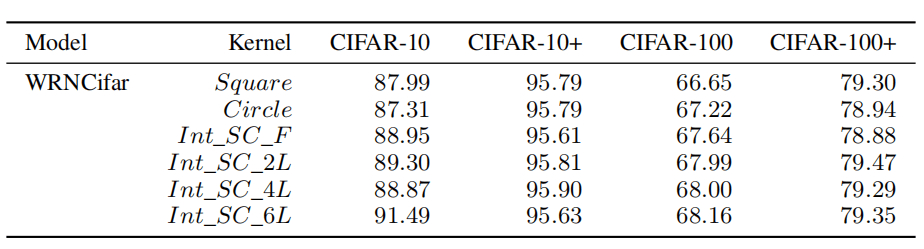
作者进一步探究了不同核的数量对实验结果的影响。在没有数据增强的情况下,随着集成核数量的增加,模型性能表现出不断增长的趋势。在有数据增强的情况下,圆核并没有展现出性能的提升。
4.5. 可视化

可以看出圆核的可视化结果明显比方核会更加精细、更容易区分物体、更加关注在图片的主体内容上。
5. 总结
基于人类的视觉感知原理,作者提出了一种更接近人类视觉感受的卷积核——圆形卷积核,作者也通过实验证明了,在没有数据增强的情况下,圆形卷积核的表现确实比方形卷积核要好。但是有了数据增强之后,圆形卷积核的性能并没有提升,反而下降了。更重要的一点是,没有数据增强集成核的性能也没有比用了数据增强方核性能要好,这就表明了,圆核带来的效益没有数据增强带来的效益高,而且圆核的效益不能和数据增强的效益兼容。
所以本质上,这篇工作只是在这个方向上开了一个头,还有很多工作可以基于本文继续开拓。另外,个人觉得,由于圆形卷积核在各个方向都是对称的,所以相比于方形卷积核,圆形确实更适合作为感受野的形状。
参考文献
[1]. Li, Duo, et al. “Involution: Inverting the inherence of convolution for visual recognition.” Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition . 2021.
[2]. Wenjie Luo, Yujia Li, Raquel Urtasun, and Richard Zemel. Understanding the effective receptive field in
deep convolutional neural networks. In Advances in Neural Information Processing Systems, volume 29,
pages 4898–4906, 2016.