第二次

7.假设有人做了如下的回归：
$y_i=\widehat{{\beta }_0}+\widehat{{\beta }_1}{x}_i+e_i$
其中，$y_i,x_i$分别为$Y_i,X_i$关于各自均值的离差。问$\widehat{{\beta }_0}和\widehat{{\beta }_1}$将分别取何值？

8.记样本回归模型为$Y_i=\widehat{{\beta }_0}+\widehat{{\beta }_1}{X}_i+e_i$,试证明普通最小二乘法估计的如下数值特征：
（1）估计的Y的均值等于实测的Y的均值：$\hat{Y}=\bar{Y}$;
（2）点($\bar{X}$,$\bar{Y}$)总在样本回归线上；
（3）残差和为0，从而残差的均值为0：$\Sigma e_i$=0,$\bar{e}$=0;
（4）残差与X不相关：$\Sigma e_i{X}_i=0$;
（5）残差与估计的Y不相关：$\Sigma e_i\widehat{Y_i}=0$;
（6）残差项与Y离差的估计不相关：$\Sigma e_i\widehat{y_i}=0$;

10.试证明：Y关于X的普通最小二乘回归，其可决系数$R^2$就是X与Y之间线性相关系数r的平方。

7

根据一元线性回归的最小二乘估计公式，可以得到 $\widehat{{\beta }_1}$ 和 $\widehat{{\beta }_0}$ 的表达式分别为：

其中，$\bar{x}$ 和 $\bar{y}$ 分别为 $x_i$ 和 $y_i$ 的样本均值。由题可知，$y_i$ 和 $x_i$ 分别为 $Y_i$ 和 $X_i$ 关于各自均值的离差，因此可以将 $\bar{x}=0$ 和 $\bar{y}=0$ 代入上述公式，得到：

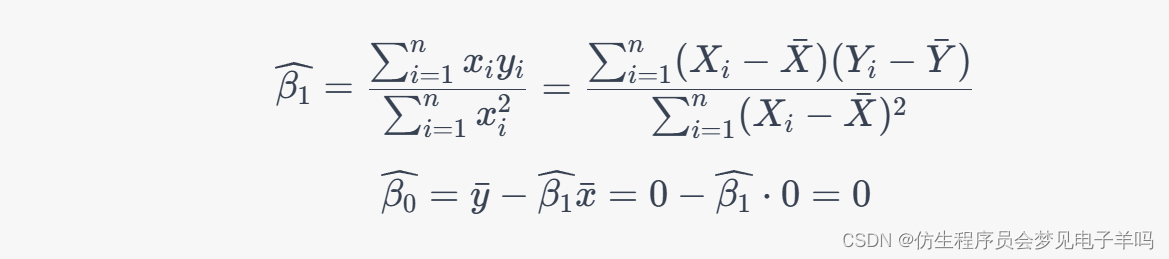
因此，$\widehat{{\beta }_0}=0$，$\widehat{{\beta }_1}$ 可以根据上述公式计算。

8

（1）估计的Y的均值等于实测的Y的均值：$\hat{Y}=\bar{Y}$

根据样本回归模型，我们有：

$$\hat{Y}=\widehat{{\beta }_0}+\widehat{{\beta }_1}X$$

其中，$\widehat{{\beta }_0}$和$\widehat{{\beta }_1}$是通过最小化残差平方和来进行估计的。因此，我们有：

$$\sum _{i=1}^n{e}_i^2=\sum _{i=1}^n(Y_i-\widehat{{\beta }_0}-\widehat{{\beta }_1}{X}_i{)}^2$$

将$\hat{Y}$代入上式，得到：

$$\sum _{i=1}^n{e}_i^2=\sum _{i=1}^n(Y_i-\hat{Y}{)}^2$$

由于$\hat{Y}$是通过最小化残差平方和来估计的，因此它是使得${\sum }_{i=1}^n(Y_i-\hat{Y}{)}^2$最小的值。这意味着$\hat{Y}$是实际Y的均值$\bar{Y}$，因为$\bar{Y}$也是使得${\sum }_{i=1}^n(Y_i-\bar{Y}{)}^2$最小的值。

因此，我们有$\hat{Y}=\bar{Y}$。

（2）点($\bar{X}$,$\bar{Y}$)总在样本回归线上

样本回归线可以表示为$Y=\widehat{{\beta }_0}+\widehat{{\beta }_1}X$。将$X$替换为$\bar{X}$，$Y$替换为$\hat{Y}$，得到：

$$\hat{Y}=\widehat{{\beta }_0}+\widehat{{\beta }_1}\bar{X}$$

由（1）可知，$\hat{Y}=\bar{Y}$，因此：

$$\bar{Y}=\widehat{{\beta }_0}+\widehat{{\beta }_1}\bar{X}$$

这意味着点($\bar{X}$,$\bar{Y}$)在样本回归线上。

（3）残差和为0，从而残差的均值为0：$\Sigma e_i$=0,$\bar{e}$=0

样本回归模型可以表示为$Y_i=\widehat{{\beta }_0}+\widehat{{\beta }_1}{X}_i+e_i$。将$\hat{Y}$代入得到：

$$e_i=Y_i-\hat{Y}=(Y_i-\bar{Y})-(\hat{Y}-\bar{Y})$$

因为$\hat{Y}=\bar{Y}$，所以：

$$e_i=(Y_i-\bar{Y})-(\bar{Y}-\hat{Y})=Y_i-\bar{Y}$$

因此，

$$\sum _{i=1}^n{e}_i=\sum _{i=1}^n(Y_i-\bar{Y})=0$$

这意味着残差的和为0，从而残差的均值为0，即$\bar{e}=0$。

（4）残差与X不相关：$\Sigma e_i{X}_i=0$

样本回归模型可以表示为$Y_i=\widehat{{\beta }_0}+\widehat{{\beta }_1}{X}_i+e_i$。将$e_i$代入得到：

$$Y_i-\widehat{{\beta }_0}-\widehat{{\beta }_1}{X}_i=e_i$$

左右两边同时乘以$X_i$：

$$X_i{Y}_i-\widehat{{\beta }_0}{X}_i-\widehat{{\beta }_1}{X}_i^2=X_i{e}_i$$

对所有的$i$进行求和：

$$\sum _{i=1}^n{X}_i{Y}_i-\widehat{{\beta }_0}\sum _{i=1}^n{X}_i-\widehat{{\beta }_1}\sum _{i=1}^n{X}_i^2=\sum _{i=1}^n{X}_i{e}_i$$

因为最小化残差平方和的条件是${\sum }_{i=1}^n{X}_i{e}_i=0$，所以：

∑ i = 1 n X i Y i − β 0 ^ ∑ i = 1 n X i −