（算法竞赛）使用广度优先搜索（BFS）解决迷宫最短路径问题

在这个充满奇思妙想的世界里，每一次探索都像是打开了一扇通往新世界的大门。今天，我们将踏上一段特别的旅程，去揭开那些隐藏在代码、算法、数学谜题或生活智慧背后的秘密。🎉😊

所以，系好安全带，准备好迎接一场充满欢笑和惊喜的冒险吧！我们的故事，现在正式开始……

题目描述

当你站在一个迷宫里的时候，往往会被错综复杂的道路弄得失去方向感，如果你能得到迷宫地图，事情就会变得非常简单。假设你已经得到了一个 n x m 的迷宫的图纸，请你找出从起点到出口的最短路。

输入：第一行是两个整数 n 和 m (1 ≤ n,m ≤ 100)，表示迷宫的行数和列数。接下来 n 行，每行一个长为 m 的字符串，表示整个迷宫的布局。字符’.‘表示空地，’#'表示墙，'S’表示起点，'T’表示出口。

输出：输出从起点到出口最少需要走的步数。

样例：输入：

复制

3 3
S#T
.#.
...

输出：

复制

来源：深搜递归广搜

在解决迷宫问题时，尤其是寻找从起点到终点的最短路径时，广度优先搜索（BFS）是一种非常高效且常用的方法。本文将详细解析一个基于 BFS 的 Python 代码，帮助你理解其工作原理和实现细节。

1. 问题背景

迷宫问题是一个经典的路径搜索问题。给定一个二维迷宫，起点为 S，终点为 T，迷宫中包含可通行的格子（用 . 表示）和障碍物（用 # 表示）。目标是找到从起点到终点的最短路径长度。

2. 为什么选择 BFS？

广度优先搜索（BFS）是一种逐层扩展的搜索算法，适用于无权图（迷宫中每个格子的移动代价相同）的最短路径问题。BFS 的核心思想是从起点开始，逐层扩展所有可能的路径，直到找到终点。由于 BFS 按层扩展，最先到达终点的路径一定是最短路径。

3. 代码解析

3.1 输入迷宫数据

Python复制
# 输入网格的行数和列数
n, m = map(int, input().split())
# 输入网格状态
a = [list(input()) for _ in range(n)]
这部分代码首先读取迷宫的行数 n 和列数 m。

然后逐行读取迷宫的布局，存储为一个二维字符数组 a。每个格子的值可以是：

S：起点。

T：终点。

.：可通行的格子。

#：障碍物。

3.2 定义方向数组

Python复制
# 定义方向数组
dx = [0, 0, 1, -1]  # 行变化（右、左、下、上）
dy = [1, -1, 0, 0]  # 列变化
这两个数组定义了四个可能的移动方向：右、左、下、上。

通过索引 i，可以从 dx 和 dy 中获取对应方向的行和列偏移量。

3.3 找到起点和终点

Python复制
# 找到起点 'S' 和终点 'T' 的位置
start_x, start_y = None, None
end_x, end_y = None, None
for i in range(n):for j in range(m):if a[i][j] == 'S':start_x, start_y = i, jelif a[i][j] == 'T':end_x, end_y = i, j
遍历迷宫，找到起点 S 和终点 T 的坐标。

如果迷宫中不存在起点或终点，程序将无法正常运行，因此需要确保输入的迷宫包含 S 和 T。

3.4 初始化访问标记数组

Python复制
# 初始化访问标记数组
vis = [[False] * m for _ in range(n)]
创建一个与迷宫大小相同的二维数组 vis，用于记录每个格子是否被访问过。

初始时，所有格子标记为未访问（False）。

3.5 BFS 函数实现

Python复制
from collections import dequedef bfs(start_x, start_y):queue = deque([(start_x, start_y, 0)])  # 队列中存储 (x, y, 步数)vis[start_x][start_y] = True  # 标记起点为已访问while queue:xx, yy, steps = queue.popleft()  # 当前格子及步数# 如果到达终点，返回步数if xx == end_x and yy == end_y:return steps# 遍历四个方向for i in range(4):x, y = xx + dx[i], yy + dy[i]if 0 <= x < n and 0 <= y < m and not vis[x][y] and a[x][y] != '#':vis[x][y] = True  # 标记为已访问queue.append((x, y, steps + 1))  # 加入队列并步数加1return -1  # 如果没有找到路径，返回 -1
队列初始化：使用 deque 创建一个队列，初始时将起点 (start_x, start_y) 和步数 0 加入队列。

逐层扩展：从队列中取出一个格子 (xx, yy)，检查是否到达终点。如果是，则返回当前步数。

扩展相邻格子：对于当前格子的四个相邻格子，检查是否在迷宫范围内、未被访问且不是障碍物。如果是，则标记为已访问，并将其加入队列，步数加1。

回溯：如果队列为空且未找到终点，返回 -1，表示无路径。

3.6 调用 BFS 并输出结果

Python复制
# 从起点开始 BFS
if start_x is not None and end_x is not None:shortest_path = bfs(start_x, start_y)print(shortest_path)
else:print("未找到起点或终点")
调用 bfs 函数，从起点开始搜索。

如果找到最短路径，输出路径长度；否则，输出提示信息。

4. 代码运行逻辑

初始化：读取迷宫数据，找到起点和终点，初始化访问标记数组。

BFS 搜索：

从起点开始，逐层扩展所有可能的路径。

使用队列存储当前层的格子及其步数。

每次从队列中取出一个格子，检查是否到达终点。

如果未到达终点，扩展其相邻格子，并将未访问的格子加入队列。

终止条件：

如果到达终点，返回当前步数。

如果队列为空且未找到终点，返回 -1。

5. 输入输出示例

输入：

复制
3 3
S#T
.#.
...
输出：
4
6. BFS 的优势

时间复杂度：BFS 的时间复杂度为 O(n×m)，适合迷宫规模较大的情况。

空间复杂度：BFS 的空间复杂度为 O(n×m)，主要用于存储访问标记数组和队列。

最短路径保证：BFS 按层扩展，最先到达终点的路径一定是最短路径。

7. 总结

本文通过详细解析基于 BFS 的代码，展示了如何高效地解决迷宫最短路径问题。BFS 的逐层扩展特性使其成为解决此类问题的理想选择。通过合理使用队列和访问标记数组，代码能够高效地找到从起点到终点的最短路径，而不会出现超时问题。

完整代码
from collections import deque# 输入网格的行数和列数
n, m = map(int, input().split())
# 输入网格状态
a = [list(input()) for _ in range(n)]# 定义方向数组
dx = [0, 0, 1, -1]  # 行变化（右、左、下、上）
dy = [1, -1, 0, 0]  # 列变化# 找到起点 'S' 和终点 'T' 的位置
start_x, start_y = None, None
end_x, end_y = None, None
for i in range(n):for j in range(m):if a[i][j] == 'S':start_x, start_y = i, jelif a[i][j] == 'T':end_x, end_y = i, j# 初始化访问标记数组
vis = [[False] * m for _ in range(n)]# BFS 函数
def bfs(start_x, start_y):queue = deque([(start_x, start_y, 0)])  # 队列中存储 (x, y, 步数)vis[start_x][start_y] = True  # 标记起点为已访问while queue:xx, yy, steps = queue.popleft()  # 当前格子及步数# 如果到达终点，返回步数if xx == end_x and yy == end_y:return steps# 遍历四个方向for i in range(4):x, y = xx + dx[i], yy + dy[i]if 0 <= x < n and 0 <= y < m and not vis[x][y] and a[x][y] != '#':vis[x][y] = True  # 标记为已访问queue.append((x, y, steps + 1))  # 加入队列并步数加1return -1  # 如果没有找到路径，返回 -1# 从起点开始 BFS
if start_x is not None and end_x is not None:shortest_path = bfs(start_x, start_y)print(shortest_path)
else:print("未找到起点或终点")

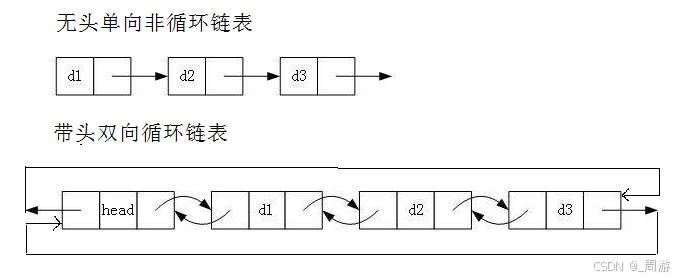
队列知识及其在广度优先搜索（BFS）中的应用

队列（Queue）是一种先进先出（First-In-First-Out，FIFO）的数据结构，广泛应用于算法和程序设计中。理解队列的使用，尤其是它在广度优先搜索（BFS）中的关键作用，对于解决路径搜索问题（如迷宫问题）至关重要。

1. 队列的基本概念

队列是一种线性数据结构，其操作类似于现实生活中的排队场景。队列的主要操作包括：

入队（Enqueue）：在队列的尾部添加一个元素。
出队（Dequeue）：从队列的头部移除一个元素。
查看队头（Peek/Front）：查看队列头部的元素，但不移除它。

队列的特点是先进先出，即最早进入队列的元素会最先被移除。

5. 使用队列的 BFS 与不使用队列的 DFS 的对比

特性	BFS（使用队列）	DFS（不使用队列）
扩展顺序	逐层扩展	深度优先
数据结构	队列（先进先出）	栈（后进先出）
适用场景	最短路径问题	所有路径问题
时间复杂度	O(n×m)	O(4n×m)
空间复杂度	O(n×m)	O(n×m)