目录

1.什么是小偷-守卫博弈？

2.用数学刻画博弈信息

3.我是小偷！

4.我是守卫！

5.尬住了。。。

6.一个感性的认识（给参数赋些值）

7.纯策略？混合策略！

8.混合策略纳什均衡求解

9.结论！！！

10.基于现实的思考

11.总结

---

1.什么是小偷-守卫博弈？

        在博弈论中，有一个经典例题，叫做小偷-守卫博弈。

        小偷-守卫博弈题目简明，但从中得出的结论足以让人思考良久。

题干如下：

---

2.用数学刻画博弈信息

        题干貌似很清晰简明，也很贴近生活，但是怎么去分析它呢，总不能“语文建模吧”（狗头）。我们可以尝试用图表把上面的信息刻画出来。

        这里所说的图表，就是博弈论中特指的“支付矩阵”，它刻画了各个博弈人采取不同策略时对应的收益情况，通常是处理博弈问题的第一步。不过要注意，支付矩阵只可以表示有限博弈。（有限博弈：博弈人数量有限、策略总数有限）

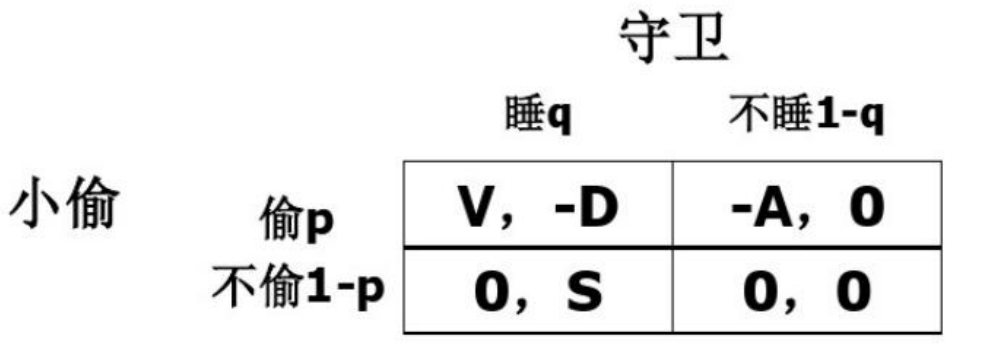
        小偷-守卫博弈是最简单的二人有限博弈，故可以很轻松地列出支付矩阵：

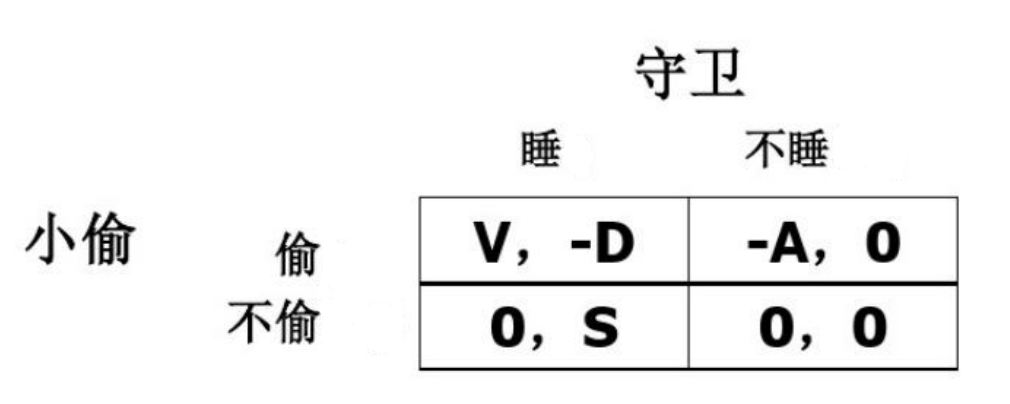
        列出支付矩阵后，需要说明的是，在每一个小方格中，左侧的值代表小偷的收益，右侧的值代表守卫的收益。四个小方格也就代表了小偷和守卫共四个不同的策略组合。

        现在一共有4个参数，大小关系未知：V,D,A,S（均为正数）。

        接下来进入角色分析环节了。

---

3.我是小偷！

        假设你作为小偷，一个很简单的问题摆在你面前：偷还是不偷？

        在思考这个问题之前，有必要先了解“严格优势策略 / 弱优势策略”的概念。

        严格优势策略：不管其他局中人选择什么策略，一个参与人选择他的某个策略给他带来的支付均高于他选择任何其他策略。

        弱优势策略：不管其他局中人选择什么策略，一个参与人选择他的某个策略给他带来的支付均不低于他选择任何其他策略。

以最为经典的二人有限博弈——囚徒困境作优势策略分析示例：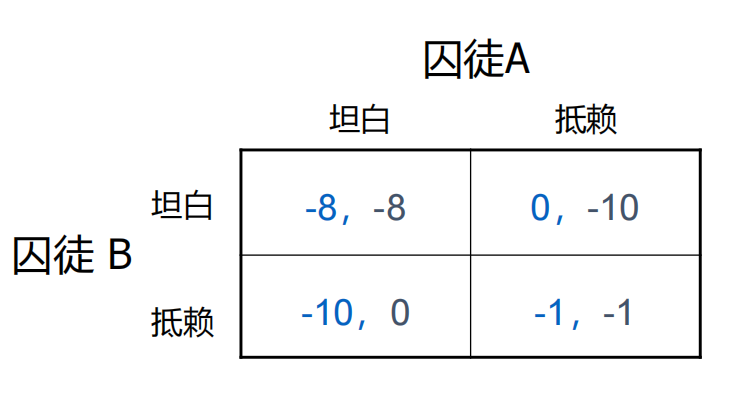

对于囚徒B来说：

        如果选择坦白，他的收益向量是 u1 = [ -8  ,  0  ]；

        如果选择抵赖，他的收益向量是 u2 = [ -10 , -1 ]；

        因为 -8 ＞ -10 , 0 ＞ -1 ,所以 u1 ＞ u2 严格成立。

        也就是对于囚徒B来说，u1的收益严格高于u2，即u1为囚徒B的严格优势策略。

        （除非囚徒B脑子有bug，否则没有任何理由不选择“坦白”策略）

对于囚徒A来说同理。

        故囚徒困境存在一个严格优势策略均衡：（坦白，坦白）。

---

        现在回到最初的小偷-守卫博弈，你变成了一个会思考、有理智的小偷。

        按照优势策略均衡的思考方式，你应该能想到以下几点：

①如果我选择偷窃，我的收益向量是 u1 = [ V , -A ]；

②如果我选择不偷，我的收益向量是 u2 = [ 0 ,   0 ]；

③因为 V ＞ 0 , -A < 0 ,所以一定不可能存在 u1 ＞ u2 或者 u1 ＞ u2 的情况。

④也就是对于我来说，在“偷”与“不偷”之间，不存在优势策略。

---

4.我是守卫！

        换位思考以下，假设你变成了一个会思考、有理智的守卫。

        按照优势策略均衡的思考方式，你同样能想到以下几点：

①如果我选择睡觉，我的收益向量是 u1 = [ -D , S ]；

②如果我选择不睡，我的收益向量是 u2 = [  0 ,  0 ]；

③因为 -D ＜ 0 , S ＞ 0 ,所以一定不可能存在 u1 ＞ u2 或者 u1 ＞ u2 的情况。

④也就是对于我来说，在“睡”与“不睡”之间，不存在优势策略。

---

5.尬住了。。。

        与囚徒困境博弈不同，小偷-守卫博弈中的两个局中人都没有优势策略可言，即不存在优势策略均衡。

        但不管你是小偷还是守卫，事件该发生的还是要发生，你仍然需要在限定时间内给出你的选择……

        那怎么办？

        抛硬币？以1/2，1/2的概率随机作出你的选择？

        还是凭自己的喜好（感性地）选择一个策略？

（可能你是一个喜欢上班摸鱼的守卫）

        ……

        当然，事情没有那么简单。

---

6.一个感性的认识（给参数赋些值）

        假设你依旧是那个聪明理智的小偷，当你看到下面两个支付矩阵时会有什么想法？

支付矩阵1：

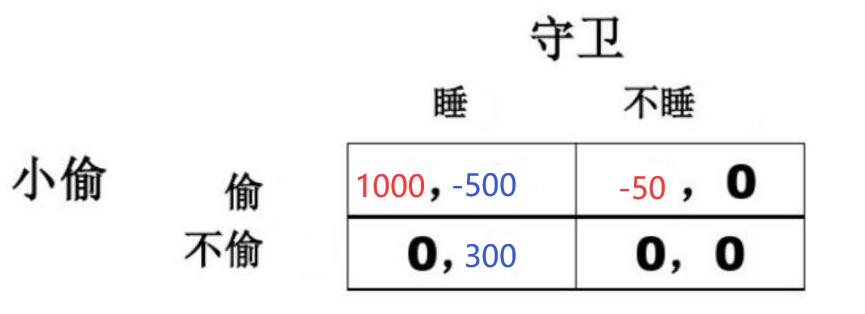
支付矩阵2： 

         

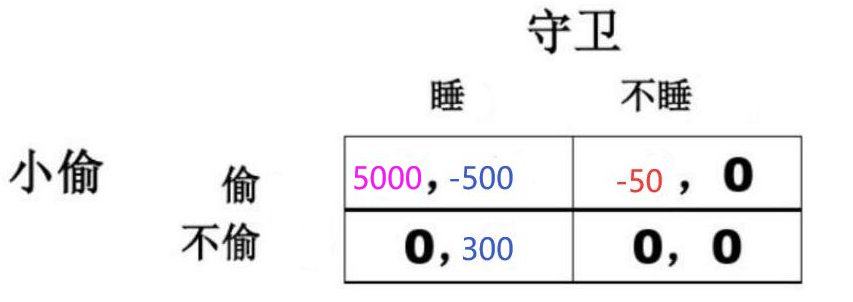
        通过对比，你的感性告诉你，你将在第2个博弈场景中大有所为——因为你对多出来的4000个单位的收益充满欲望。换句话说，你认为你更有可能在第2个博弈场景中选择偷窃行为。

        但是如果你足够聪明，你的理性会告诉你，偷窃利益的增长会引起守卫的警觉。

        守卫在第2个博弈场景中睡觉的可能性明显会小于在第1个场景中睡觉的可能性，因为理智的守卫不可能在看到偷窃利益增长的变化后毫无反应和行动。

        这样一来，你好像连这两个对比博弈场景都分析不清了……

---

        但是，你能明显感觉到，总有一种神奇的力量在控制这个博弈的结果，制约着局中人的策略。

        这种神奇的力量叫“纳什均衡”。

---

        那么小偷-守卫博弈存在纳什均衡吗？

        不存在，但又存在。

---

7.纯策略？混合策略！

       

        小偷-守卫博弈不存在优势策略均衡，并且也不存在纯策略纳什均衡。

        但是，如果你的策略并非纯策略，而是混合策略呢？

         小偷以一定的概率p选择偷窃，守卫以一定的概率q选择睡觉，则存在一对特殊p*,q*，使得双方都不愿意独自偏离自己所选定的策略，从而达到（p*,q*）的混合策略纳什均衡。

---

8.混合策略纳什均衡求解

---

小偷(p)的期望收益U1(p,q)：

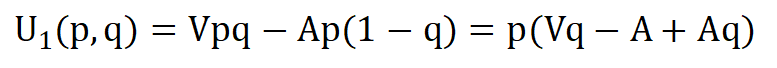
期望收益U1(p,q)对p求偏导数：

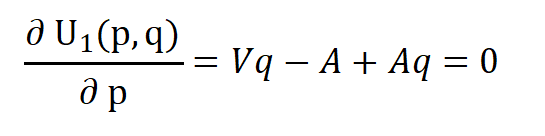
q*为候选解

---

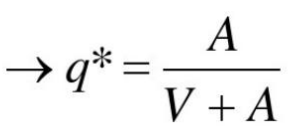
守卫(q)的期望收益U2(p,q)：

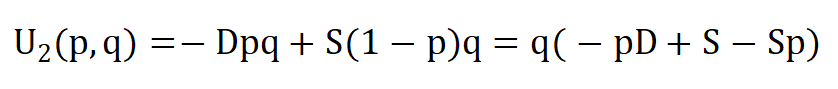
期望收益U2(p,q)对q求偏导数：

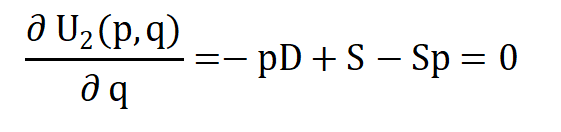
p*为候选解:

---

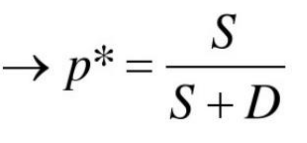
9.结论！！！

        经过验证，p*、q*均为该博弈的混合策略纳什均衡解。

        还记得这个博弈中的4个参数吗：

①V：小偷盗窃成功的收益

②D：守卫失职所造成的损失

③A：小偷被逮捕的损失

④S：守卫睡觉且无事发生的收益

假定：V（偷窃收益）    和    S（睡觉收益）        为不可变参数；

           A（对小偷的惩罚）和 D（对守卫的惩罚）为可变参数。

---

你应该可以得出以下结论：

        让人感到诡异的是：加大对小偷的处罚，不仅无法降低偷窃事件的发生率，反倒会使守卫偷懒的概率增加；加大对守卫的处罚，不会降低守卫偷懒的概率，但是却能使偷窃事件的发生率下降！

<摘自：倪玉平.“激励的悖论”——试论清代的盐业缉私[J].盐业史研究,2006(04):3-7.>

---

10.基于现实的思考

        基于“小偷-守卫博弈”的现实场景和理论模型还是有较大差别的，如在监考人员履职的例子中，不能强行套用模型结论，认为加大对学生作弊的处罚有害而无利，这于我们的直觉和人类社会的基本规律相违背。

        造成这种现象的原因可以归纳为以下几点：

①现实场景并不是理想的两人（监考人员、考生）博弈，有国家调控和干预

（监考人员的责任感并不会因为考生选择策略的不同而发生显著的变化）

②局中人并不是绝对理性的，存在心理威慑效应

（加大对局中人犯错的处罚可以明显地改变其策略的偏向程度）

③人类社会伦理需要

（社会伦理与良知不允许政府的政策纵容错误事件的发生）

        因此，这两种调控手段需要双管齐下，才能达到预期的效果。这是符合博弈理论的，也是符合社会伦理道德的。

ps：我在寒假发过一篇教育法治的文章，涉及到学生考试作弊的处罚问题。

（关键词：高校、学位、学术自治、刑法）

链接：案例分析（第4期）

---

11.总结

        小偷-守卫博弈在双方采用纯策略的情况下不存在纳什均衡，但在双方采用混合策略的情况下存在纳什均衡，且双方都没有动机偏离该纳什均衡。

        从结果上看，“加大对小偷的处罚，无法降低偷窃事件的发生率，反倒会使守卫偷懒的概率增加”和“加大对守卫的处罚，不会降低守卫偷懒的概率，但是却能使偷窃事件的发生率下降”这两个结论在理论层面反映了“激励悖论”存在的真实性，给生活中的许多问题提供了可参考的指导思想。

        但是真实场景中环境的复杂性也使得博弈原理更为复杂，需要兼顾多方面的影响，而且要考虑人的感性因素。

        小偷-守卫博弈是一个简单的问题，也将一直是博弈论中永恒的经典，并不断给人类带来感性的挑战和理性的思考。