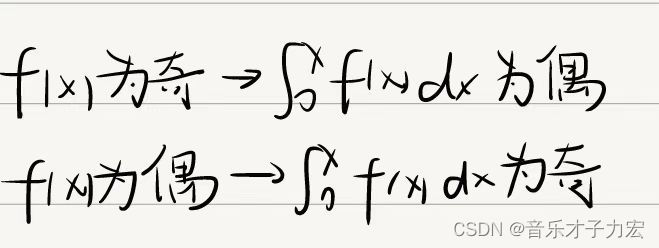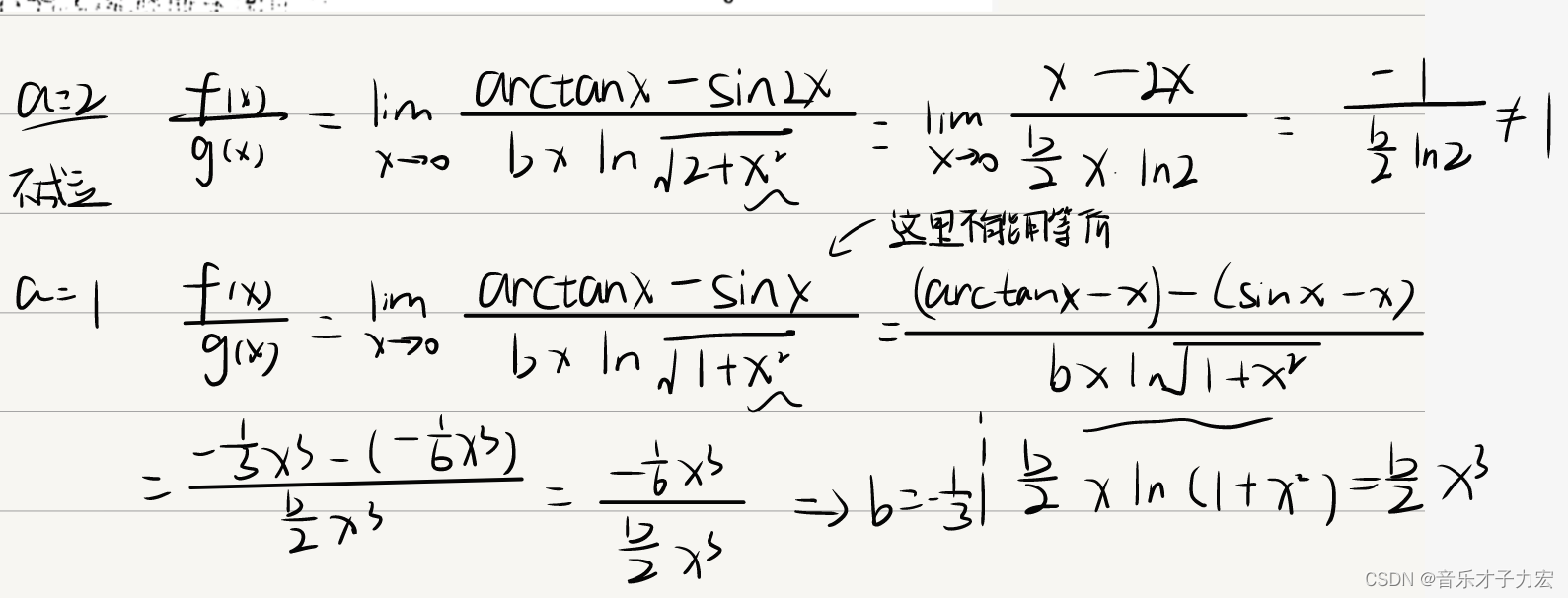第一章 函数 极限 连续(选择题部分):
问题描述

问题分析:
思路:判断ABC三个选项比较复杂,D选项易于判断
解决方法:
问题描述

问题分析:
定理:若f(x)在(a,b)连续,且f(a+0),f(b-0)存在→f(a,b)上有界(反之不成立 例:sinx在(0,+∞)上有界但在x→∞时振荡 极限不存在)
解决方法:
问题描述

问题分析:
解决方法:
A和B选项无法确定内部函数的奇偶性,所以无法判断
问题描述

问题分析:
ABC选项可以找到特例(平时要积累),D选项用反证法
解决方法:
问题描述

解决方法:
(A)选项由上题的B选项可知不成立
(B)反证 否则Xn 和 Yn 都是有界变量→Xn x Yn为有界 不成立
(C)反证 则Yn为有界变量,无穷小x有界还是无穷小
(D)Xn/Xn*Yn 有界比无穷→0 所以1/Yn→0 所以 Yn→无穷
问题描述

问题分析:
An可以通过 夹逼 来推出Bn收敛 ,Bn可以通过单调 有界来推出An收敛,所以C正确
解决方法:
(A)令An和Bn都等于n 则数列不收敛 所以不成立
(B)令An和Bn都等于1 则数列不发散 所以不成立
问题描述

问题分析:
这些等式存在的条件是 x→趋近于0 但是x 不能等于0 所以ABCD没有一个对
问题描述

问题分析:
运用两个等价代换的公式
解决方法:
问题描述

问题分析:
不可以直接对ln(1+2x)做等价代换成2x,因为未知的f(x)存在不知道具体的比例关系
解决方法:
方法一:加上一个2x再减去一个2x
方法二:泰勒公式展开ln(1+2x)
方法三:去掉极限在等式的右边加上一个高阶无穷小 a(x)(通法)
问题描述

问题分析:
首先可以通过第一个极限中对1-cosx进行等价变换可看出 f(x)等价与x的平方
n阶无穷小意味着原式对x的n次方的比例为常数项
对x→0 0/0 的情况有三种方法 1.洛必塔 2.泰勒 3. 无穷小替换 这里只能用一次洛必塔因为
f(x)连续,它的导函数不一定连续
解决方法:
方法一:用f(x)等价与x的平方来做
方法二:f(x)→0 ,f(x)等价于g(x),则f(x)从0到x的积分 等价于g(x)从0到x的积分
方法三:
方法四:排除法 直接把f(x)=x的平方 带进去进行计算
问题描述
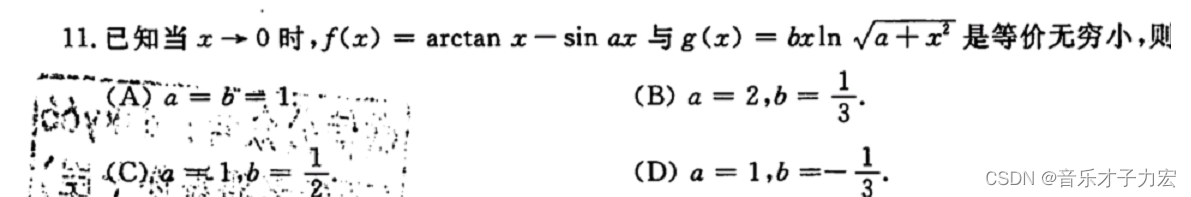
问题分析:
通过观察选项可知a要么为2 或 为1 所以可以直接将a=2带入计算,不成立 则a=1
等价无穷小两者比值为1 (同阶为常数项)
加减等价代换的条件 a-b 则 等价的函数 a*/b* 之比不等于1
解决方法:
问题描述

问题分析:
一开始看到f(x)等价代换后两式相减为0 有点懵逼,导致没有思路
后面发现对于有sinx tanx 之间相加减等式可以用加x再减x来凑等价无穷小的替换