文章目录
- 第八讲 一元函数积分学的概念与计算
- 不定积分
- 原函数(不定积分)存在定理
- 用导数介值定理解释
- 定积分
- 变限积分
- 不定积分与变限积分的比较
- 积分的奇偶性
- 积分的周期性
- 反常积分
- 基本积分公式
- 基本积分方法
- 凑微分法
- 换元法
- 分部积分法:
- 有理函数的积分
- 定积分的计算
- 区间再现公式
- 华里氏(点火)公式
- 例题精选
第八讲 一元函数积分学的概念与计算
不定积分


不定积分包含了一个函数的全体原函数,它们只差一个常数C
原函数(不定积分)存在定理






用导数介值定理解释

如果fx可导,如果它能取到两个端点的导数值,则必然能取到这两个导数值内的所有的值。
而原函数求导等于其儿子函数:

如果一个函数可导,它是不可能导出这样的儿子的:
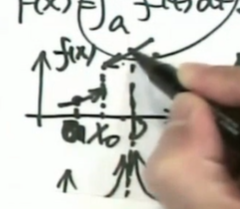
因为根据导数介值定理,要求其取遍所有的导数值,在这里明显不行。
因此有跳跃间断点的函数,它的父亲无法满足求导处处等于儿子,没有这样的父亲能满足条件,所以它是孤儿
可去间断点也是同理,因为可去间断点在该点没有定义,或者函数值可以任意取,
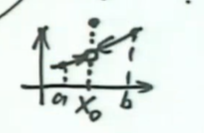
那么对于这里的x0来讲,f(x0)这个函数值,是无法通过父亲的F’(x0)得出来的。
而对于无穷间断点来说,极限不存在,也就是fx当x趋于零时,fx不存在,那么FX就不可能可导
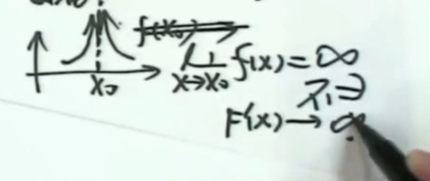
所以说如果一个函数可导,它是导不出带有可去、跳跃、和无穷间断点的函数的。
但是一个函数可导,有可能可以导出带有振荡间断点的函数。
例如:

首先这个函数是可导的。
但是这时候这个导函数带有振荡间断点:
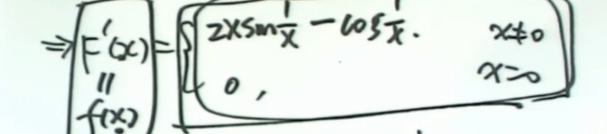
并且它不会违背导数介值定理:

所以函数求导的函数,要么是连续函数,要么是带有振荡间断点的函数。
定积分
需要注意的是 定积分的几何意义是一个面积,(但可以为负),也就是说是一个数
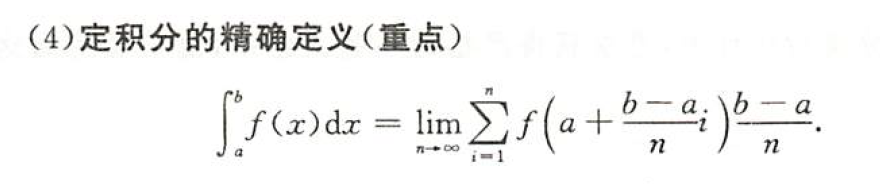


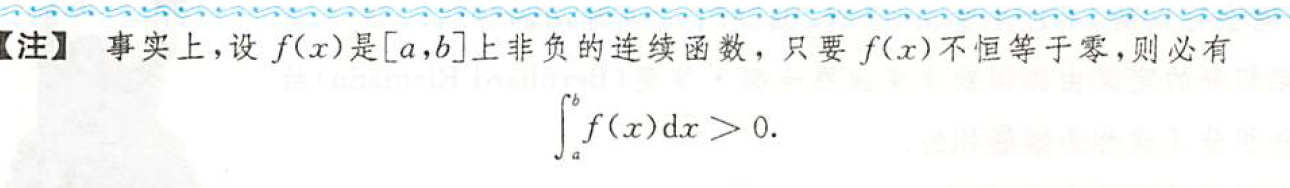
↑这是一个重要结论
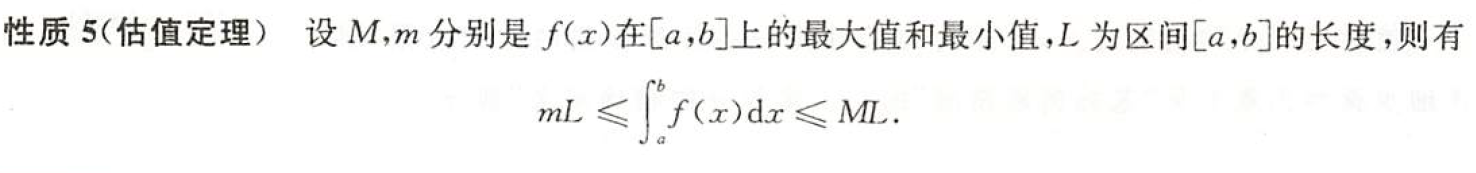
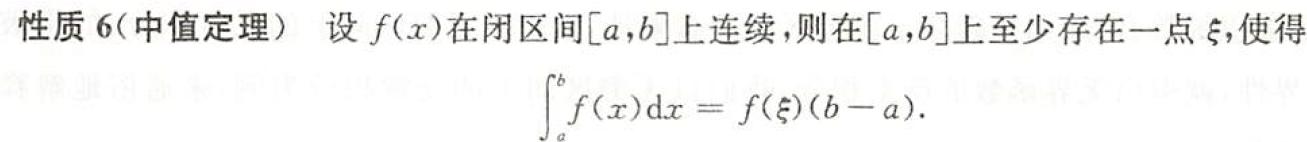
中值定理,核心考点!
证明:用拉格朗日

变限积分
变限积分是在定积分中,将积分上限从常数改为x,此时可以得到一个关于x的函数
而在变限积分中,由于下限选取的不同,会导致他们在常数上会有所差异,但是他们都是它的原函数,求导还是等于该函数
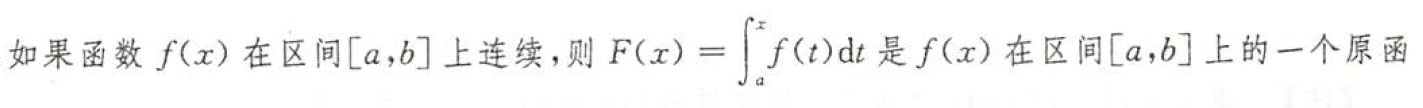
这两个都是e的x²的父亲,他们只是差了一个

不定积分与变限积分的比较
不定积分的∫号没有上下限,但是变上限积分下限为常数,上限为x
不定积分代表的是这个函数的全体原函数,而变上限积分是其中一个原函数。
积分的奇偶性

上面是下限为0的情况,但如果下限不是0而是一个常数,则


对于下面这种情况,要求积分在0到a上积分为零,可以是a=0,也可以是这样:因为这两种情况,积分得到的函数值相同,(也就是常数是一样的,在这里那个常数C都等于0)

或者还可以这样理解,在图上,你从0开始计算面积,和从2开始计算面积,得到的结果是一样的。
这也很好理解,奇函数如果往上平移则不是奇函数了。

复合函数的奇偶性:只与外层有关
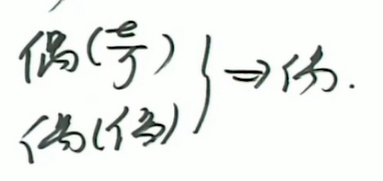
积分的周期性

一个函数以T为周期,导函数必然以T为周期,但父亲函数只有在满足红圈条件下才以T为周期。

积分的可拆性:
只要起点终点相同,中间可以随便拆:

根据可拆性,这里拆成这样三部分(因为要保留0到T的部分)

同时上面这个定理说明一个周期函数的积分长度若为T,则积分值与起点无关
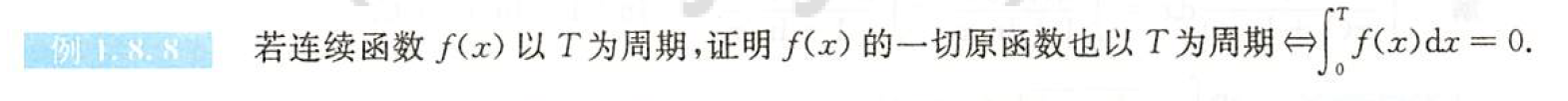

如果fx以T为周期,那么在fx一个周期上积分为零和其原函数是周期函数互为充要条件


反常积分
又称黎曼积分,可以在无穷区间或者无界函数上进行积分,这种情况下,可能也可以积分出一个数来。

其实就是从代入数变成代入极限
基本积分公式
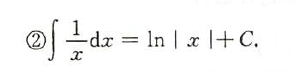
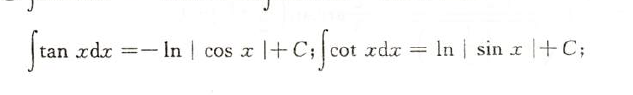




基本积分方法
凑微分法



换元法


secx的图像:




可能需要经过计算才能从a²x+bx+c变成4-(x+1)²这样
此时就需要令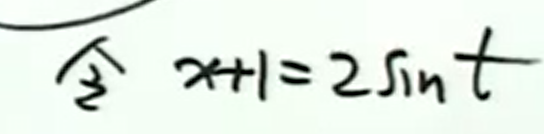

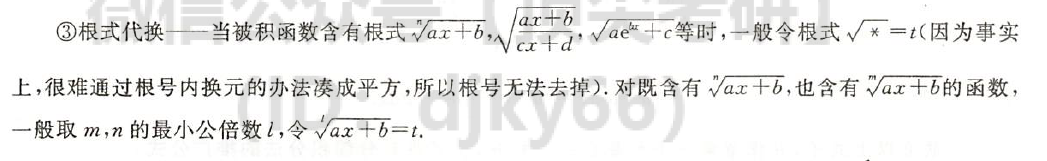


金字塔形较为稳定,不适合改变,此时可以通过倒代换来改变。
分部积分法:
’就是d()/dx的简写



更适合积分的来做v 越靠近右边越适合做v
表格法:



对于指数函数和三角函数积分

算完之后再移回去

总共有这三种类型的考题

对于反三角和对数函数,求导一次后就可以结束了,然后进行表格积分法

例题



有理函数的积分


例题:



定积分的计算


第四第五个很重要
区间再现公式

但是这个也并不好求
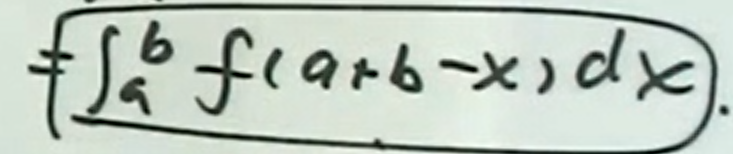
但是这两个加起来



例题

用第一问的结论来解决第二问

在0到nT上积分相当于n个周期的和

在这里还可以

华里氏(点火)公式




这里也用了区间再现公式

但是在使用点火公式前 可能会这样,设一些步骤让你做


还有这种

用一系列计算阻挡着你
或者右图 心形线旋转一周算旋转体体积
例题精选


可以从两个角度:根据答案图像来判断斜率,也可以通过所给图像来想象出答案












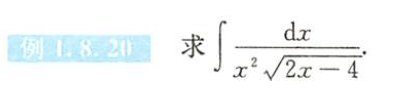



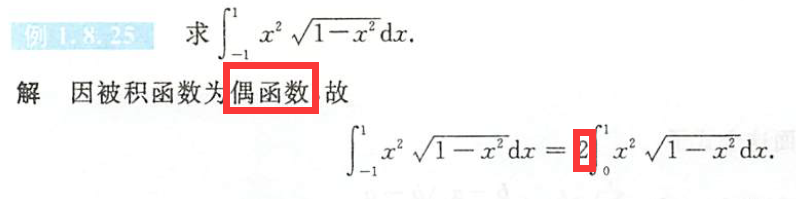

下面这道难点题











反常积分: