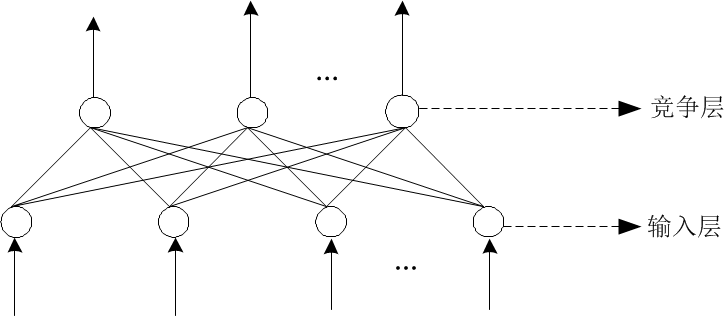
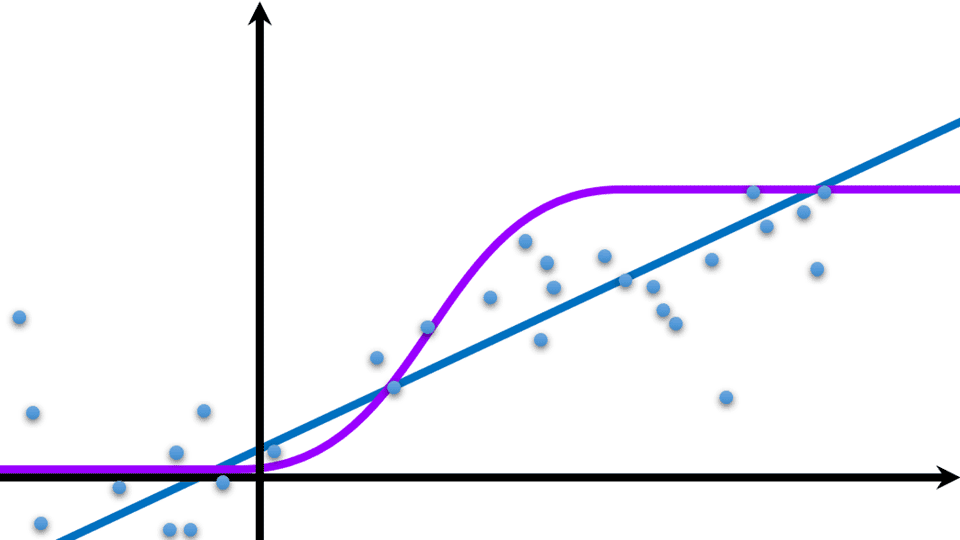
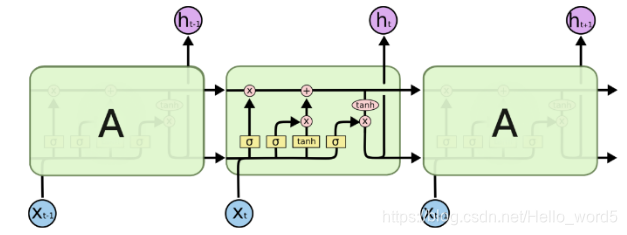
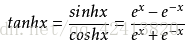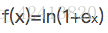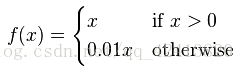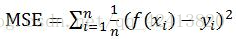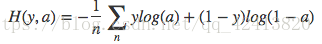先来看一下单个神经元网络模型：

其中 xi 表示输入，wi 和 b 表示参数。图中下方的公式是 1 函数的模型，嗯，就是一个线性模型。那么就这么一个简单的线性模型怎么仿真出人类神经元那么复杂的玩意儿呢？一个线性模型当然满足不了，这不就有了函数 2。函数 2 这类的函数我们常称之为 激活函数 或者 激励函数。那么有人又问了你怎么知道图中那一大堆 wi 和 b 参数到底取值是什么，别急，网络模型的训练就是为了找出这些值，这就引出了网络模型训练过程中的 损失函数 和 梯度下降 (或者其他优化方式) 用于求解这些值。上面讲的只是一个神经元，要解决更加复杂的问题，就需要很多这种神经元组成的一层或多层神经网络结构。下面会对出现的概念做一个简单的介绍。

1）正向传播

      数据从输入到输出的流向传递过程为正向传播。它是在一个假设由合适的w和b的基础上，才可以实现对现实环境的正确拟合。但是在实际过程中，我们无法得知w和b的值具体是多少才算是正常的。于是加入了一个训练过程，通过反向误差传递的方法让模型自动来修正，最终产生一个合适的权重。 

2）反向传播

 

      反向传播的意义–告诉模型我们需要将w和b调整到多少。在刚开始没有得到合适的权重时，正向传播生成的结果与实际的标签是有误差的，反向传播就是要把这个误差传递给权重，让权重做适当的调整来达到一个合适的输出。

      如何将输出的权重误差转化为权重误差，使用的是BP算法，又称“误差反向传播算法”。

     反向传播的核心思想：让正向传播的输出结果与标签间的误差最小化。 

      为了让损失值（将输出值与标签直接相减，或是做平方差等运算）变得最小，我们运用数学知识，选择一个损失值的表达式，也就是损失函数，让这个函数有最小值，接着通过求导的方式，找到最小值处函数切线斜率（也就是梯度) , 从而让w和b的值沿着这个梯度来调整。 
      至于每次调整多少，我们引入一个叫做“学习率”的参数，这样通过不断的迭代，使误差逐步接近最小值，最终达到我们的目标。

3）激活函数

      激活函数的主要作用就是用来加入非线性因素的，以解决线性模型表达能力不足的缺陷，在整个神经网络里起到至关重要的作用。 
      因为神经网络的数学基础是处处可微的，所以选取的激活函数要能保证数据输入与输出也是可微的。 

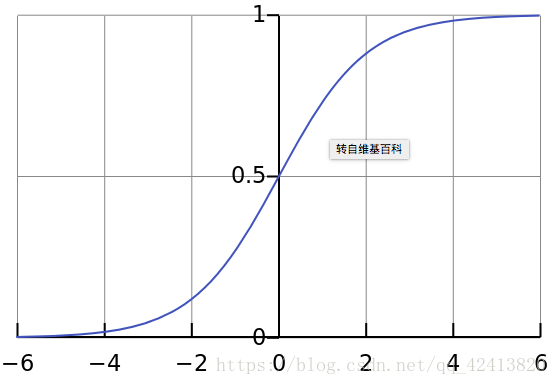
 1) sigmoid 函数 或者叫做 Logistic 函数

公式：

图形：

特点：从图像可以看出当 x 趋近于正负无穷时，y 值趋近于 1 或 -1，这种情况就是饱和状态。一旦达到这种状态意味着再增大 x 值，y 值基本就不会变化了，这也就会导致了向底层传递的梯度也变得非常小，网络参数很难得到有效训练，这种现象就是梯度消失。此外，sigmoid函数的输出均大于0，使得输出均值不是0，这称为偏移现象，这会导致后一层的神经元将得到上一层输出的非0均值的信号作为输入。

 2）tanh 函数

公式：

tanh(x) = 2sigmoid(2x) - 1

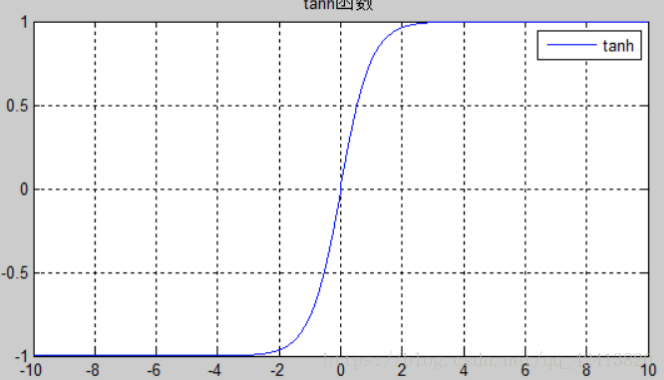
图形：

特点：tanh可以说是sigmoid函数的升级版。与sigmoid相比，它的输出均值是0，使得其收敛速度要比sigmoid               快，减少迭代次数。然而，tanh一样具有饱和状态，从而造成梯度消失。

 3）relu 函数  Rectified Linear Units

公式：  f(x) = max(0, x)

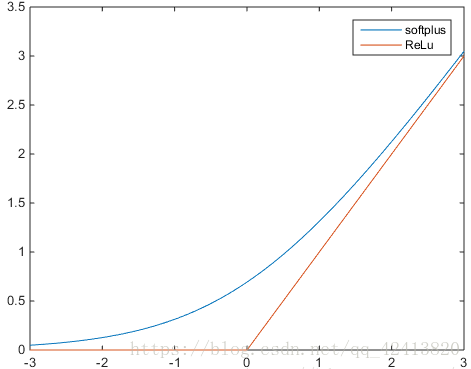
图形：

特点：当x<0时，relu硬饱和，而当x>0时，则不存在饱和问题。所以，relu 能够在x>0时保持梯度不衰减，从而缓解梯度消失问题，然而，随着训练的推进，部分输入会落入硬饱和区，导致对应权重无法更新。这种现象称为“神经元死亡”。与sigmoid类似，relu的输出均值也大于0，偏移现象和神经元死亡会共同影响网络的收敛性。

        图中还显示了一个softplus函数，其更加平滑，但是计算量很大。公式如下：

                                                              

relu的一些演化函数：

Noisy relus： 为max中的 x 添加一个高斯分布的噪声   

                        

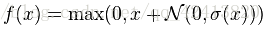
Leaky relus：让 x 为负值时乘以 0.01 ，使其对负值不是一味的拒绝，而是缩小

                      

进一步让0.01变成一个可调的数值：   f(x) = max(0, ax)

对 x 小于0时做更复杂的变化：

                      

4）损失函数

    用于描述模型预测值与真实值的差距大小，一般常见的有两种算法----均值平方差(MSE) 和 交叉熵。

    1）均值平方差(Mean Squared Error)，也成为'均方误差'。在神经网络中表达预测值与真实值之间的差异，在数理统计中，是指参数估计值与参数真值之差平方的期望。

                                          

        f(xi)为预测值，yi为真值。

    2）交叉熵

        一般用在分类问题上，表达的意思为预测输入样本属于某一类的概率。

        y代表真实值的分类，a代表预测值。                   

                      

     损失算法的选取：

         损失函数的选取取决于输入标签数据的类型，如果输入的是实数、无界值，损失函数使用平方差，如果输入标签是矢量(分类标志)，使用交叉熵会更合适。          

5）梯度下降

      梯度下降是一个最优化算法，通常也称为最速下降法，常用于机器学习和人工智能中递归性地逼近最小偏差模型，梯度下降地方向也就是用负梯度方向为搜索方向，沿着梯度下降地方向求极小值。 
在训练过程中，每次的正向传播后都会得到输出值与真实值的损失值，这个损失值越小，代表模型越好，于是梯度下降的算法就用在这里，帮助寻找最小的那个损失值，从而可以反推出对应的学习参数w和b，达到优化模型的效果。 
      常用的梯度下降方法可以分为：批量梯度下降、随机梯度下降和小批量梯度下降。