各位CSDN的uu们好呀,今天,小雅兰的内容仍然是数据结构与算法专栏的排序呀,下面,让我们进入归并排序的世界吧!!!
归并排序
归并排序(MERGE-SORT)是建立在归并操作上的一种有效的排序算法,该算法是采用分治法(Divide and Conquer)的一个非常典型的应用。将已有序的子序列合并,得到完全有序的序列;即先使每个子序列有序,再使子序列段间有序。若将两个有序表合并成一个有序表,称为二路归并。 归并排序核心步骤:
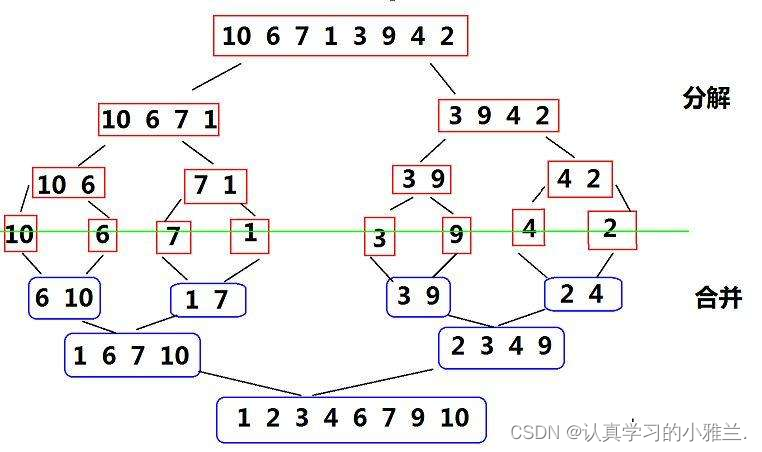
void _MergeSort(int* a, int begin, int end, int* tmp) {if (begin >= end){return;}int mid = (begin + end) / 2;//[begin,mid] [mid+1,end]_MergeSort(a, begin, mid, tmp);_MergeSort(a, mid + 1, end, tmp);//归并两个区间int begin1 = begin;int begin2 = mid + 1;int end1 = mid;int end2 = end;int i = begin;while (begin1 <= end1 && begin2 <= end2){if (a[begin1] < a[begin2]){tmp[i++] = a[begin1++];}else{tmp[i++] = a[begin2++];}}while (begin1 <= end1){tmp[i++] = a[begin1++];}while (begin2 <= end2){tmp[i++] = a[begin2++];}memcpy(a + begin, tmp + begin, sizeof(int) * (end - begin + 1)); } //归并排序 void MergeSort(int* a, int n) {int* tmp = (int*)malloc(sizeof(int) * n);_MergeSort(a, 0, n - 1, tmp);free(tmp); }
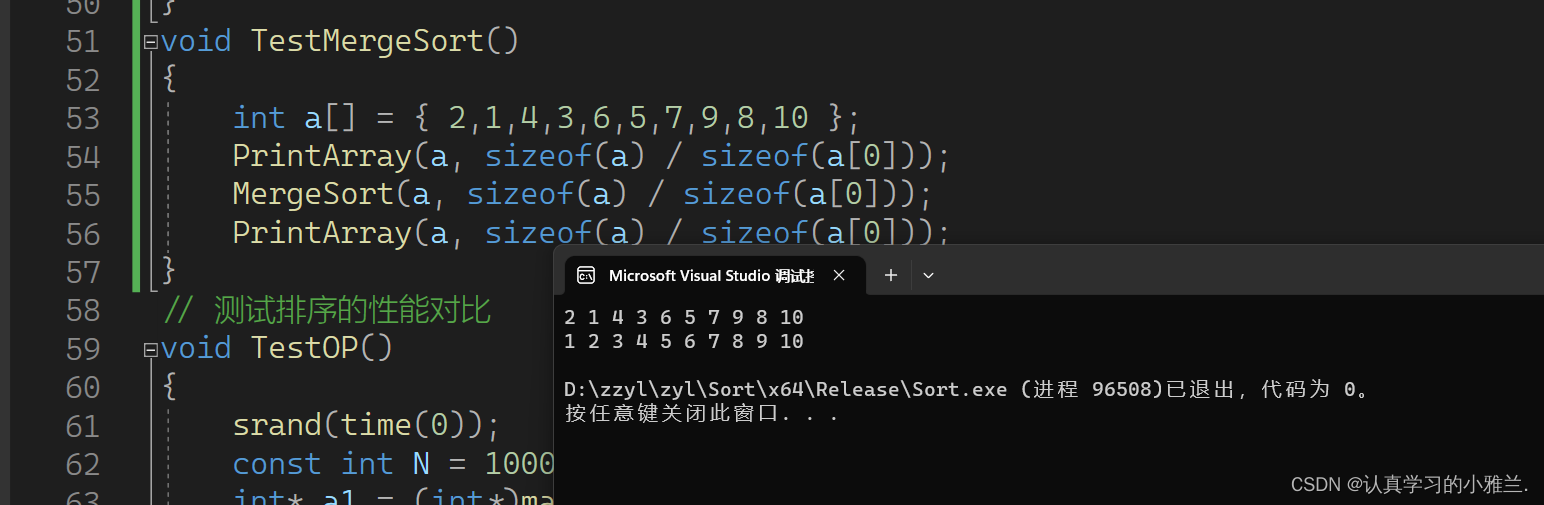
测试一下归并排序:
void TestMergeSort()
{
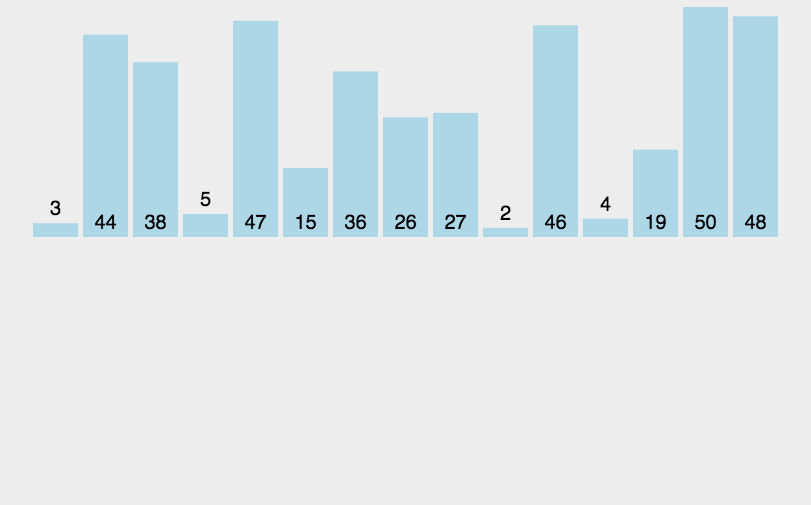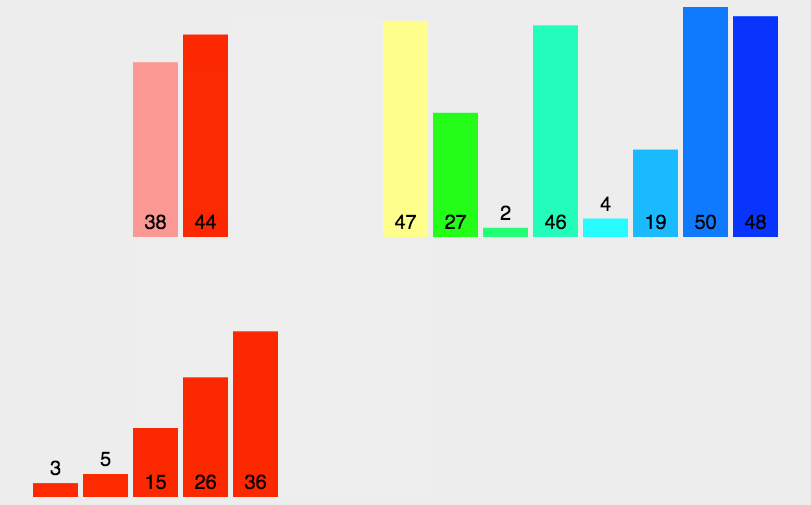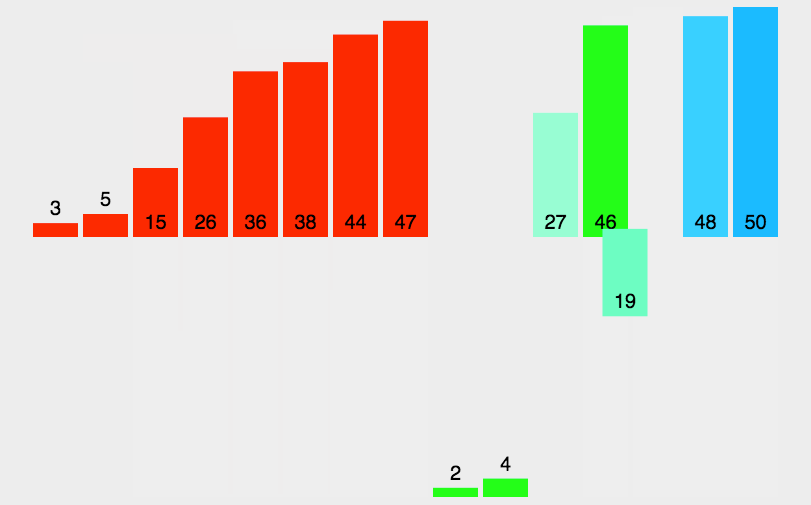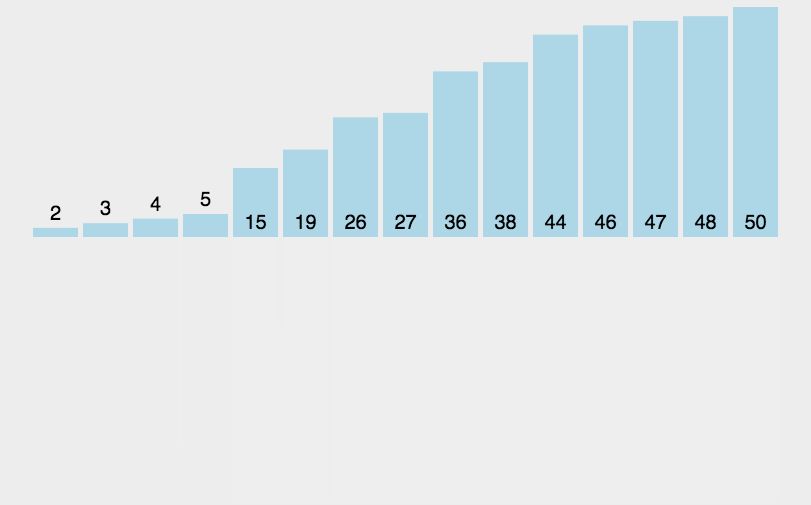
int a[] = { 2,1,4,3,6,5,7,9,8,10 };
PrintArray(a, sizeof(a) / sizeof(a[0]));
MergeSort(a, sizeof(a) / sizeof(a[0]));
PrintArray(a, sizeof(a) / sizeof(a[0]));
}
归并排序的特性总结:
- 归并的缺点在于需要O(N)的空间复杂度,归并排序的思考更多的是解决在磁盘中的外排序问题。
- 时间复杂度:O(N*logN)
- 空间复杂度:O(N)
- 稳定性:稳定
归并排序非递归
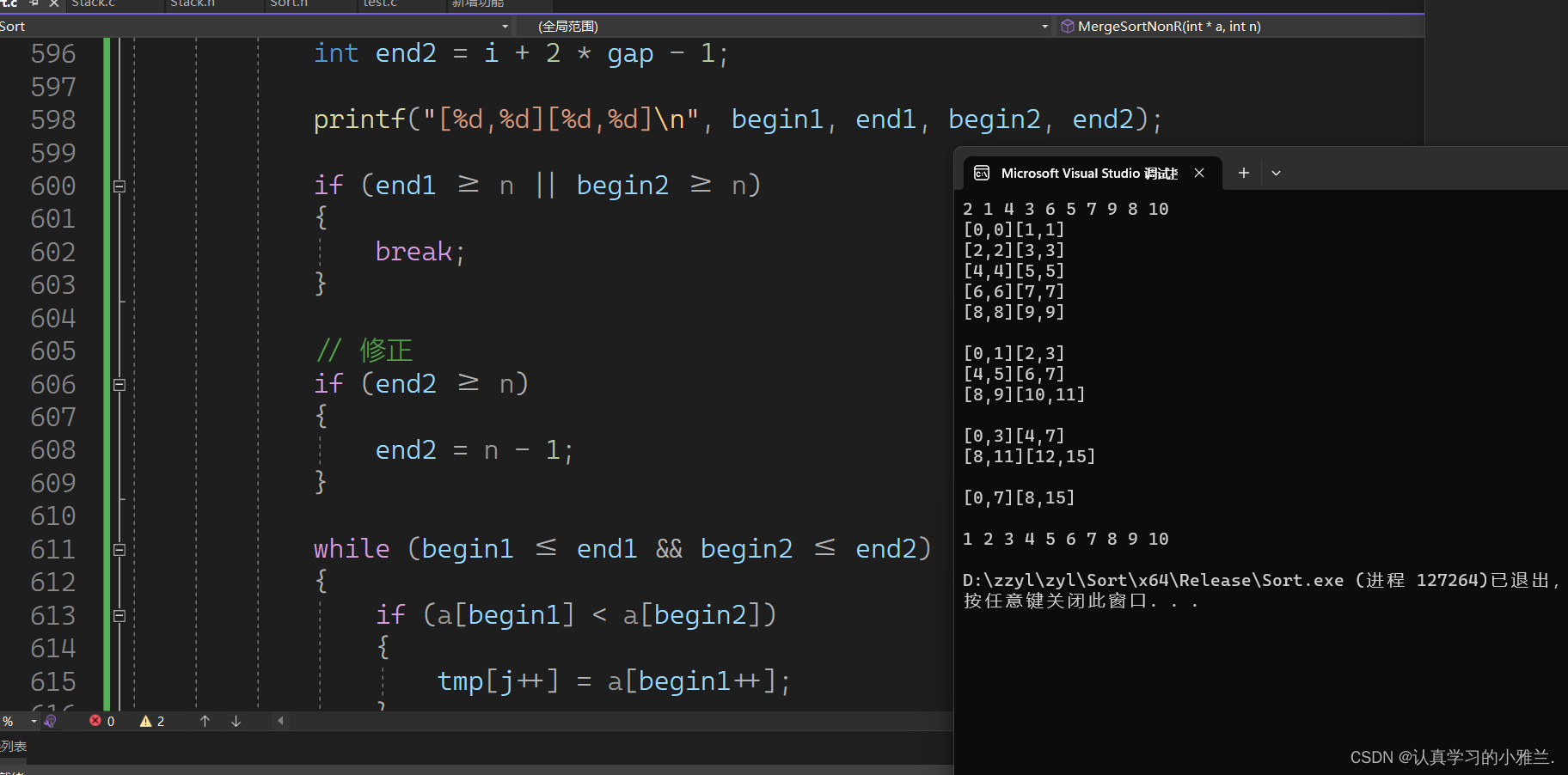
void MergeSortNonR(int* a, int n) {int* tmp = (int*)malloc(sizeof(int) * n);if (tmp == NULL){perror("malloc失败!!!");return;}int gap = 1;while (gap < n){int j = 0;for (int i = 0; i < n; i += gap){//每组的合并数据int begin1 = i;int end1 = i + gap - 1;int begin2 = i + gap;int end2 = i + 2 * gap - 1;while (begin1 <= end1 && begin2 <= end2){if (a[begin1] < a[begin2]){tmp[j++] = a[begin1++];}else{tmp[j++] = a[begin2++];}}while (begin1 <= end1){tmp[j++] = a[begin1++];}while (begin2 <= end2){tmp[j++] = a[begin2++];}}memcpy(a, tmp, sizeof(int) * n);gap *= 2;}free(tmp); }但是这个代码是有非常严重的越界问题的,只有有2的次方的数据的时候,才不会越界!!!
小雅兰在这里打印几组数据看得更加清楚:
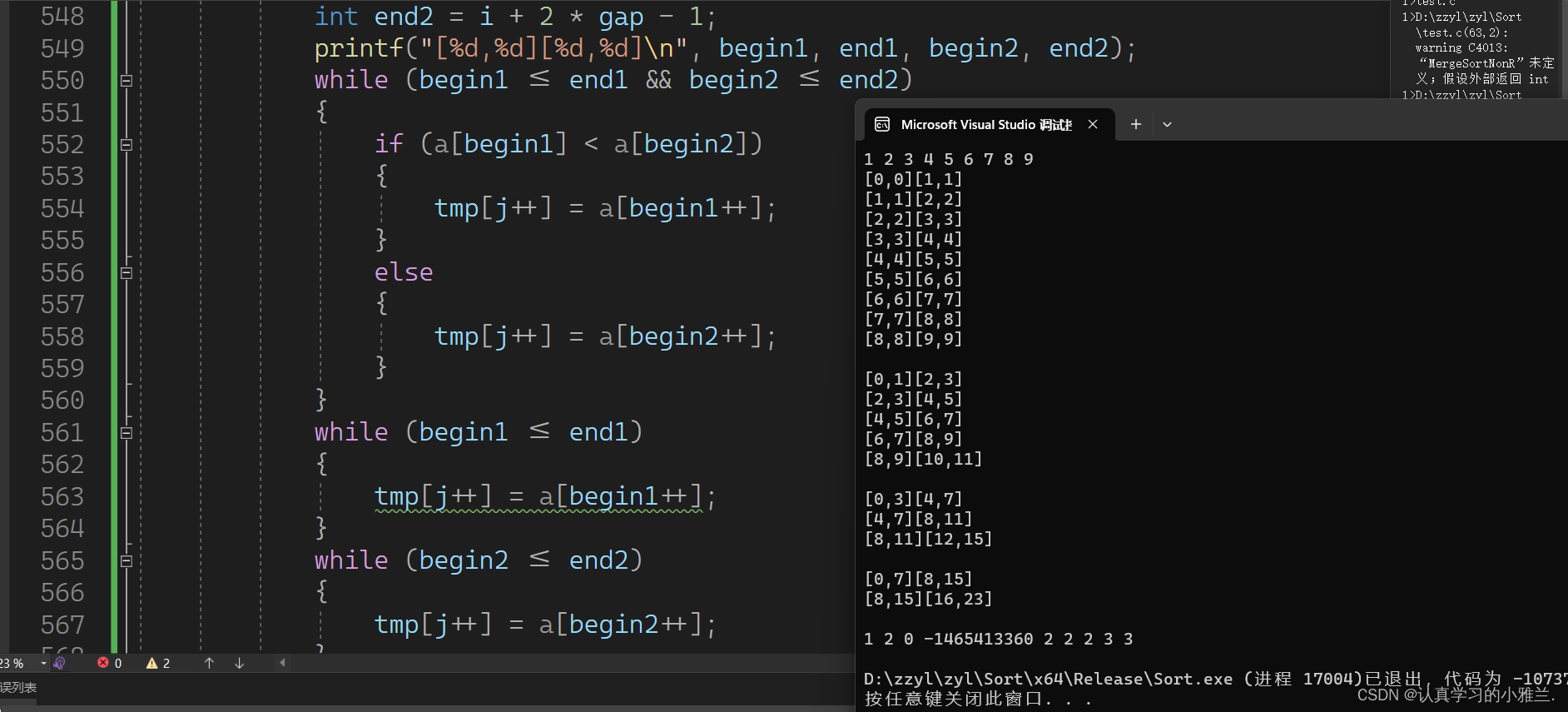
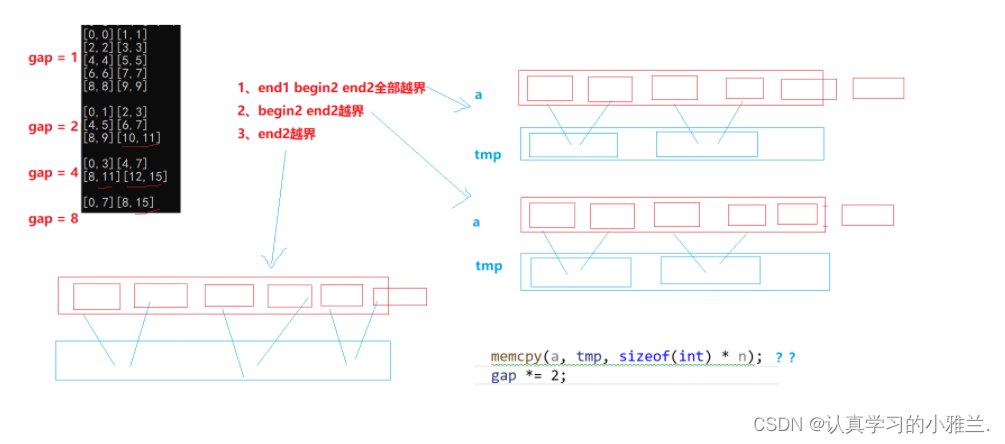
void MergeSortNonR(int* a, int n) {int* tmp = (int*)malloc(sizeof(int) * n);if (tmp == NULL){perror("malloc失败!!!");return;}// 1 2 4 ....int gap = 1;while (gap < n){int j = 0;for (int i = 0; i < n; i += 2 * gap){// 每组的合并数据int begin1 = i;int end1 = i + gap - 1;int begin2 = i + gap;int end2 = i + 2 * gap - 1;printf("[%d,%d][%d,%d]\n", begin1, end1, begin2, end2);if (end1 >= n || begin2 >= n){break;}// 修正if (end2 >= n){end2 = n - 1;}while (begin1 <= end1 && begin2 <= end2){if (a[begin1] < a[begin2]){tmp[j++] = a[begin1++];}else{tmp[j++] = a[begin2++];}}while (begin1 <= end1){tmp[j++] = a[begin1++];}while (begin2 <= end2){tmp[j++] = a[begin2++];}// 归并一组,拷贝一组memcpy(a + i, tmp + i, sizeof(int) * (end2 - i + 1));}printf("\n");gap *= 2;}free(tmp); }这样修正一下就可以啦!!!
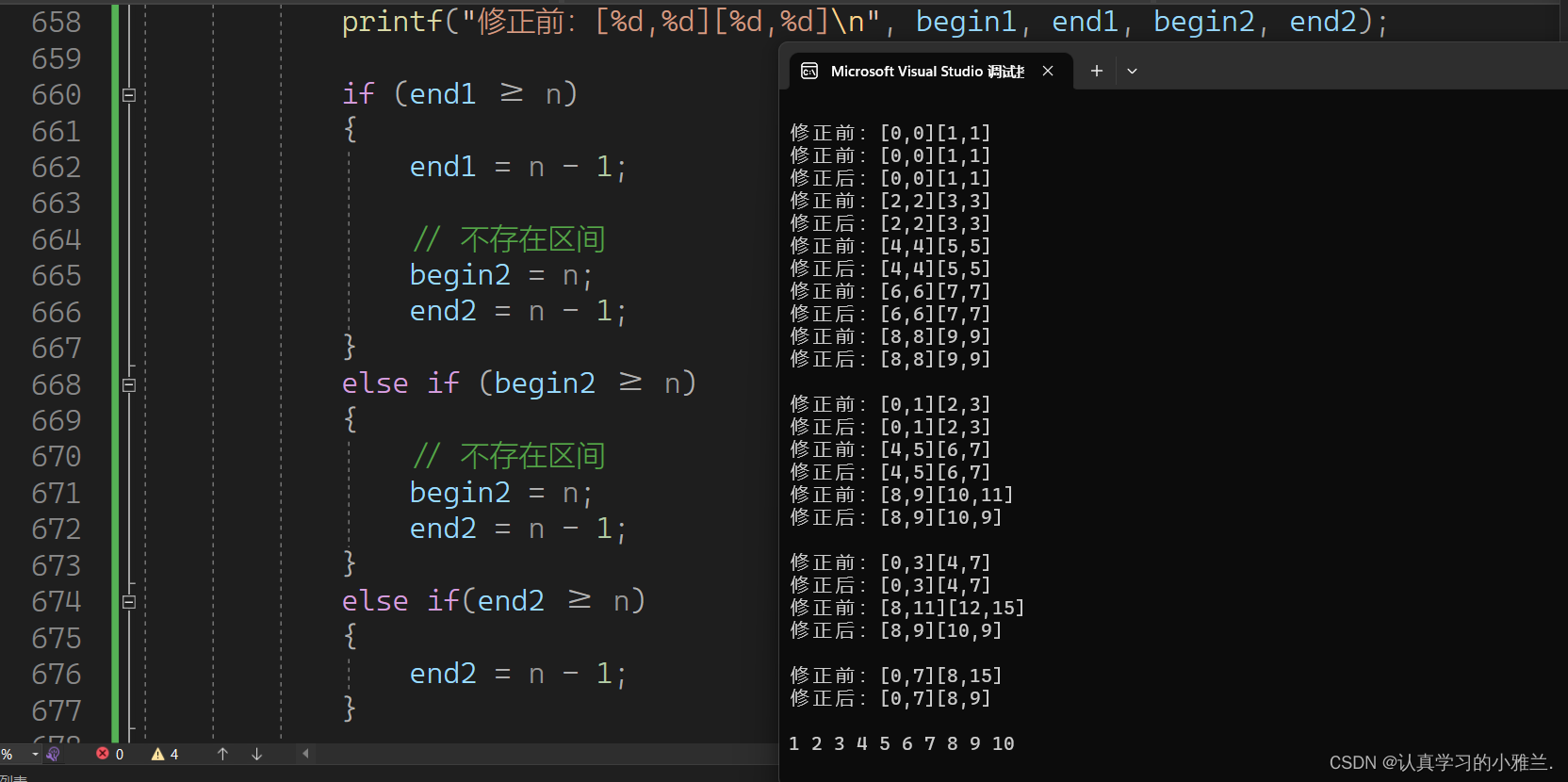
这个越界问题还有第二种解决方案:
void MergeSortNonR(int* a, int n) {int* tmp = (int*)malloc(sizeof(int) * n);// 1 2 4 ....int gap = 1;while (gap < n){int j = 0;for (int i = 0; i < n; i += 2 * gap){// 每组的合并数据int begin1 = i, end1 = i + gap - 1;int begin2 = i + gap, end2 = i + 2 * gap - 1;printf("修正前:[%d,%d][%d,%d]\n", begin1, end1, begin2, end2);if (end1 >= n){end1 = n - 1;// 不存在区间begin2 = n;end2 = n - 1;}else if (begin2 >= n){// 不存在区间begin2 = n;end2 = n - 1;}else if(end2 >= n){end2 = n - 1;}printf("修正后:[%d,%d][%d,%d]\n", begin1, end1, begin2, end2);while (begin1 <= end1 && begin2 <= end2){if (a[begin1] <= a[begin2]){tmp[j++] = a[begin1++];}else{tmp[j++] = a[begin2++];}}while (begin1 <= end1){tmp[j++] = a[begin1++];}while (begin2 <= end2){tmp[j++] = a[begin2++];}}printf("\n");memcpy(a, tmp, sizeof(int) * n);gap *= 2;}free(tmp); }
测试各种排序
// 测试排序的性能对比 void TestOP() {srand(time(0));const int N = 1000000;int* a1 = (int*)malloc(sizeof(int) * N);int* a2 = (int*)malloc(sizeof(int) * N);int* a3 = (int*)malloc(sizeof(int) * N);int* a4 = (int*)malloc(sizeof(int) * N);int* a5 = (int*)malloc(sizeof(int) * N);int* a6 = (int*)malloc(sizeof(int) * N);int* a7 = (int*)malloc(sizeof(int) * N);for (int i = 0; i < N; ++i){a1[i] = rand();a2[i] = a1[i];a3[i] = a1[i];a4[i] = a1[i];a5[i] = a1[i];a6[i] = a1[i];a7[i] = a1[i];}int begin1 = clock();InsertSort(a1, N);int end1 = clock();int begin2 = clock();ShellSort(a2, N);int end2 = clock();int begin3 = clock();SelectSort(a3, N);int end3 = clock();int begin4 = clock();HeapSort(a4, N);int end4 = clock();int begin5 = clock();QuickSort(a5, 0, N - 1);int end5 = clock();int begin6 = clock();MergeSort(a6, N);int end6 = clock();int begin7 = clock();BubbleSort(a7, N);int end7 = clock();printf("InsertSort:%d\n", end1 - begin1);printf("ShellSort:%d\n", end2 - begin2);printf("SelectSort:%d\n", end3 - begin3);printf("HeapSort:%d\n", end4 - begin4);printf("QuickSort:%d\n", end5 - begin5);printf("MergeSort:%d\n", end6 - begin6);printf("BubbleSort:%d\n", end7 - begin7);free(a1);free(a2);free(a3);free(a4);free(a5);free(a6);free(a7); }
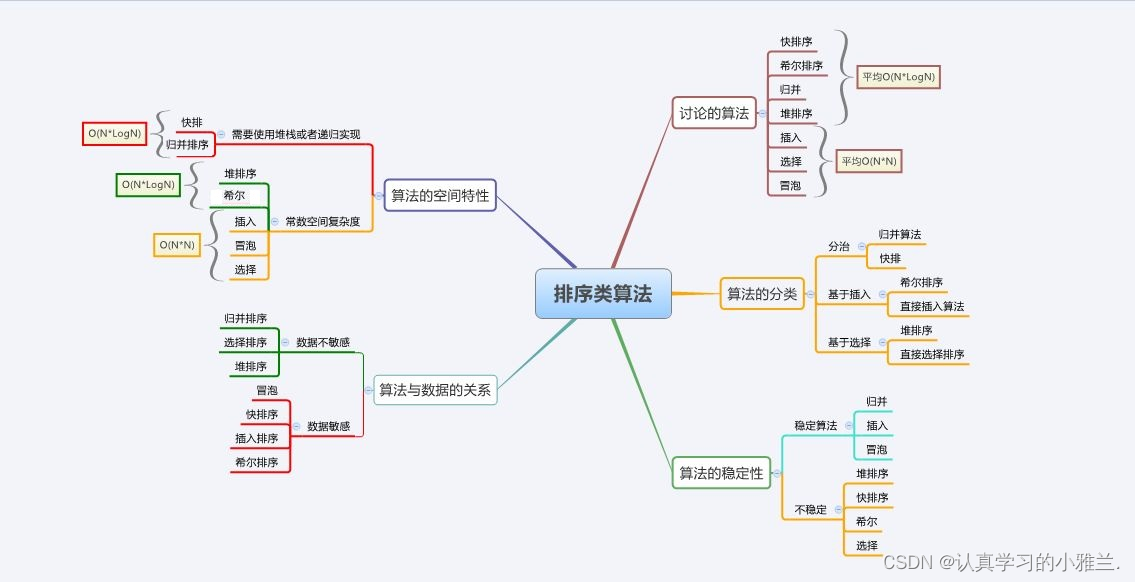

所有排序源代码:
Sort.h的内容:
#pragma once
#include<stdio.h>
#include<stdlib.h>
#include<time.h>
#include<stdbool.h>
#include<string.h>
void PrintArray(int* a, int n);
// 直接插入排序
void InsertSort(int* a, int n);// 希尔排序
void ShellSort(int* a, int n);// 直接选择排序
void SelectSort(int* a, int n);// 堆排序
void AdjustDown(int* a, int n, int root);
void HeapSort(int* a, int n);// 冒泡排序
void BubbleSort(int* a, int n);//快速排序
int PartSort1(int* a, int left, int right);
int PartSort2(int* a, int left, int right);
int PartSort3(int* a, int left, int right);
void QuickSort(int* a, int begin, int end);void QuickSortNonR(int* a, int begin, int end);
//归并排序
void MergeSort(int* a, int n);void MergeSortNonR(int* a, int n);
Sort.c的内容:
#include"Sort.h"
#include"Stack.h"
void PrintArray(int* a, int n)
{
int i = 0;
for (i = 0; i < n; i++)
{
printf("%d ", a[i]);
}
printf("\n");
}
//直接插入排序
void InsertSort(int* a, int n)
{
int i = 0;
for (i = 1; i < n; i++)
{
int end = i - 1;
int tmp = a[i];
while (end >= 0)
{
//插入的数据比原来的数据小
if (a[end] > tmp)
{
a[end + 1] = a[end];
--end;
}
else
{
break;
}
}
a[end + 1] = tmp;
}
}
//希尔排序
void ShellSort(int* a, int n)
{
//1.gap>1,预排序
//2.gap==1,直接插入排序
int gap = n;
while (gap > 1)
{
gap = gap / 3 + 1;
//+1可以保证最后一次一定是1
for (int i = 0; i < n - gap; i++)
{
int end = i;
int tmp = a[end + gap];
while (end >= 0)
{
if (a[end] > tmp)
{
a[end + gap] = a[end];
end = end - gap;
}
else
{
break;
}
}
a[end + gap] = tmp;
}
}
}
//冒泡排序
void BubbleSort(int* a, int n)
{
for (int j = 0; j < n; j++)
{
bool exchange = false;
for (int i = 1; i < n - j; i++)
{
if (a[i - 1] > a[i])
{
int tmp = a[i];
a[i] = a[i - 1];
a[i - 1] = tmp;
exchange = true;
}
}
if (exchange == false)
{
break;
}
}
}
void Swap(int* a1, int* a2)
{
int tmp = *a1;
*a1 = *a2;
*a2 = tmp;
}//直接选择排序
void SelectSort(int* a, int n)
{
int begin = 0;
int end = n - 1;
while (begin < end)
{
int maxi = begin;
int mini = begin;
for (int i = begin; i <= end; i++)
{
if (a[i] > a[maxi])
{
maxi = i;
}
if (a[i] < a[mini])
{
mini = i;
}
}
Swap(&a[begin], &a[mini]);
//如果maxi和begin重叠,修正一下即可
if (begin ==maxi)
{
maxi = mini;
}
Swap(&a[end], &a[maxi]);
++begin;
--end;
}
}//向下调整算法
void AdjustDown(int* a, int n, int parent)
{
//默认左孩子小
int child = parent * 2 + 1;
while (child < n)//孩子在数组范围内
{
//选出左右孩子中大的那一个
//有可能假设错了
//左孩子不存在,一定没有右孩子——完全二叉树
//左孩子存在,有可能没有右孩子
if (child + 1 < n && a[child + 1] > a[child])
// 右孩子存在 右孩子>左孩子
//不能这么写 if (a[child + 1] > a[chid] && child + 1 < n )
//这样写会有越界的风险 因为是先访问了数组中的元素 再去比较右孩子是否存在
{
++child;
}
//child就是大的那个孩子
//不关心到底是左孩子还是右孩子
if (a[child] > a[parent])
{
Swap(&a[child], &a[parent]);
parent = child;
child = parent * 2 + 1;//默认又算的是左孩子
}
else
{
break;
}}
}
//堆排序
void HeapSort(int* a, int n)
{
//建堆——向下调整建堆
int i = 0;
for (i = (n - 1 - 1) / 2; i >= 0; i--)
{
AdjustDown(a, n, i);
}
//升序——建大堆
int end = n - 1;
while (end > 0)
{
Swap(&a[0], &a[end]);
AdjustDown(a, end, 0);
--end;
}
}//三数取中
int GetMidIndex(int* a, int left, int right)
{
int mid = (left + right) / 2;
if (a[left] < a[mid])
{
if (a[mid] < a[right])
{
return mid;
}
else if (a[left] < a[right])
{
return right;
}
else
{
return left;
}
}
else // a[left] > a[mid]
{
if (a[mid] > a[right])
{
return mid;
}
else if (a[left] > a[right])
{
return right;
}
else
{
return left;
}
}
}
// hoare
// [left, right]
int PartSort1(int* a, int left, int right)
{
int midi = GetMidIndex(a, left, right);
Swap(&a[left], &a[midi]);int keyi = left;
while (left < right)
{
// 右边找小
while (left < right && a[right] >= a[keyi])
{
--right;
}// 左边找大
while (left < right && a[left] <= a[keyi])
{
++left;
}Swap(&a[left], &a[right]);
}Swap(&a[keyi], &a[left]);
return left;
}
挖坑法
[left, right]
//int PartSort2(int* a, int left, int right)
//{
// int midi = GetMidIndex(a, left, right);
// Swap(&a[left], &a[midi]);
//
// int key = a[left];
// int hole = left;
// while (left < right)
// {
// // 右边找小
// while (left < right && a[right] >= key)
// {
// --right;
// }
//
// a[hole] = a[right];
// hole = right;
//
// // 左边找大
// while (left < right && a[left] <= key)
// {
// ++left;
// }
//
// a[hole] = a[left];
// hole = left;
// }
//
// a[hole] = key;
//
// return hole;
//}
//
前后指针法
[left, right]
//int PartSort3(int* a, int left, int right)
//{
// int midi = GetMidIndex(a, left, right);
// Swap(&a[left], &a[midi]);
//
// int prev = left;
// int cur = left + 1;
// int keyi = left;
// while (cur <= right)
// {
// if (a[cur] < a[keyi] && ++prev != cur)
// {
// Swap(&a[prev], &a[cur]);
// }
//
// ++cur;
// }
//
// Swap(&a[prev], &a[keyi]);
// keyi = prev;
// return keyi;
//}
//快速排序
void QuickSort(int* a, int begin, int end)
{
if (begin >= end)
{
return;
}
int keyi = PartSort1(a, begin, end);
//[begin,keyi-1] keyi [keyi+1,end]
QuickSort(a, begin, keyi - 1);
QuickSort(a, keyi + 1, end);
}
//快速排序非递归
void QuickSortNonR(int* a, int begin, int end)
{
Stack st;
StackInit(&st);
StackPush(&st, end);
StackPush(&st, begin);while (!StackEmpty(&st))
{
int left = StackTop(&st);
StackPop(&st);int right = StackTop(&st);
StackPop(&st);int keyi = PartSort1(a, left, right);
// [left, keyi-1] keyi [keyi+1, right]
if (keyi + 1 < right)
{
StackPush(&st, right);
StackPush(&st, keyi + 1);
}if (left < keyi - 1)
{
StackPush(&st, keyi - 1);
StackPush(&st, left);
}
}StackDestroy(&st);
}
void _MergeSort(int* a, int begin, int end, int* tmp)
{
if (begin >= end)
{
return;
}
int mid = (begin + end) / 2;
//[begin,mid] [mid+1,end]
_MergeSort(a, begin, mid, tmp);
_MergeSort(a, mid + 1, end, tmp);
//归并两个区间
int begin1 = begin;
int begin2 = mid + 1;
int end1 = mid;
int end2 = end;
int i = begin;
while (begin1 <= end1 && begin2 <= end2)
{
if (a[begin1] < a[begin2])
{
tmp[i++] = a[begin1++];
}
else
{
tmp[i++] = a[begin2++];
}
}
while (begin1 <= end1)
{
tmp[i++] = a[begin1++];
}
while (begin2 <= end2)
{
tmp[i++] = a[begin2++];
}
memcpy(a + begin, tmp + begin, sizeof(int) * (end - begin + 1));
}
//归并排序
void MergeSort(int* a, int n)
{
int* tmp = (int*)malloc(sizeof(int) * n);
if (tmp == NULL)
{
perror("malloc失败!!!");
return;
}
_MergeSort(a, 0, n - 1, tmp);
free(tmp);
}//归并排序非递归
void MergeSortNonR(int* a, int n)
{
int* tmp = (int*)malloc(sizeof(int) * n);// 1 2 4 ....
int gap = 1;
while (gap < n)
{
int j = 0;
for (int i = 0; i < n; i += 2 * gap)
{
// 每组的合并数据
int begin1 = i, end1 = i + gap - 1;
int begin2 = i + gap, end2 = i + 2 * gap - 1;printf("修正前:[%d,%d][%d,%d]\n", begin1, end1, begin2, end2);
if (end1 >= n)
{
end1 = n - 1;// 不存在区间
begin2 = n;
end2 = n - 1;
}
else if (begin2 >= n)
{
// 不存在区间
begin2 = n;
end2 = n - 1;
}
else if(end2 >= n)
{
end2 = n - 1;
}printf("修正后:[%d,%d][%d,%d]\n", begin1, end1, begin2, end2);
while (begin1 <= end1 && begin2 <= end2)
{
if (a[begin1] <= a[begin2])
{
tmp[j++] = a[begin1++];
}
else
{
tmp[j++] = a[begin2++];
}
}while (begin1 <= end1)
{
tmp[j++] = a[begin1++];
}while (begin2 <= end2)
{
tmp[j++] = a[begin2++];
}
}
printf("\n");memcpy(a, tmp, sizeof(int) * n);
gap *= 2;
}free(tmp);
}
//void MergeSortNonR(int* a, int n)
//{
// int* tmp = (int*)malloc(sizeof(int) * n);
// if (tmp == NULL)
// {
// perror("malloc失败!!!");
// return;
// }
// // 1 2 4 ....
// int gap = 1;
// while (gap < n)
// {
// int j = 0;
// for (int i = 0; i < n; i += 2 * gap)
// {
// // 每组的合并数据
// int begin1 = i;
// int end1 = i + gap - 1;
// int begin2 = i + gap;
// int end2 = i + 2 * gap - 1;
//
// printf("[%d,%d][%d,%d]\n", begin1, end1, begin2, end2);
//
// if (end1 >= n || begin2 >= n)
// {
// break;
// }
//
// // 修正
// if (end2 >= n)
// {
// end2 = n - 1;
// }
//
// while (begin1 <= end1 && begin2 <= end2)
// {
// if (a[begin1] < a[begin2])
// {
// tmp[j++] = a[begin1++];
// }
// else
// {
// tmp[j++] = a[begin2++];
// }
// }
//
// while (begin1 <= end1)
// {
// tmp[j++] = a[begin1++];
// }
//
// while (begin2 <= end2)
// {
// tmp[j++] = a[begin2++];
// }
//
// // 归并一组,拷贝一组
// memcpy(a + i, tmp + i, sizeof(int) * (end2 - i + 1));
// }
// printf("\n");
// gap *= 2;
// }
// free(tmp);
//}
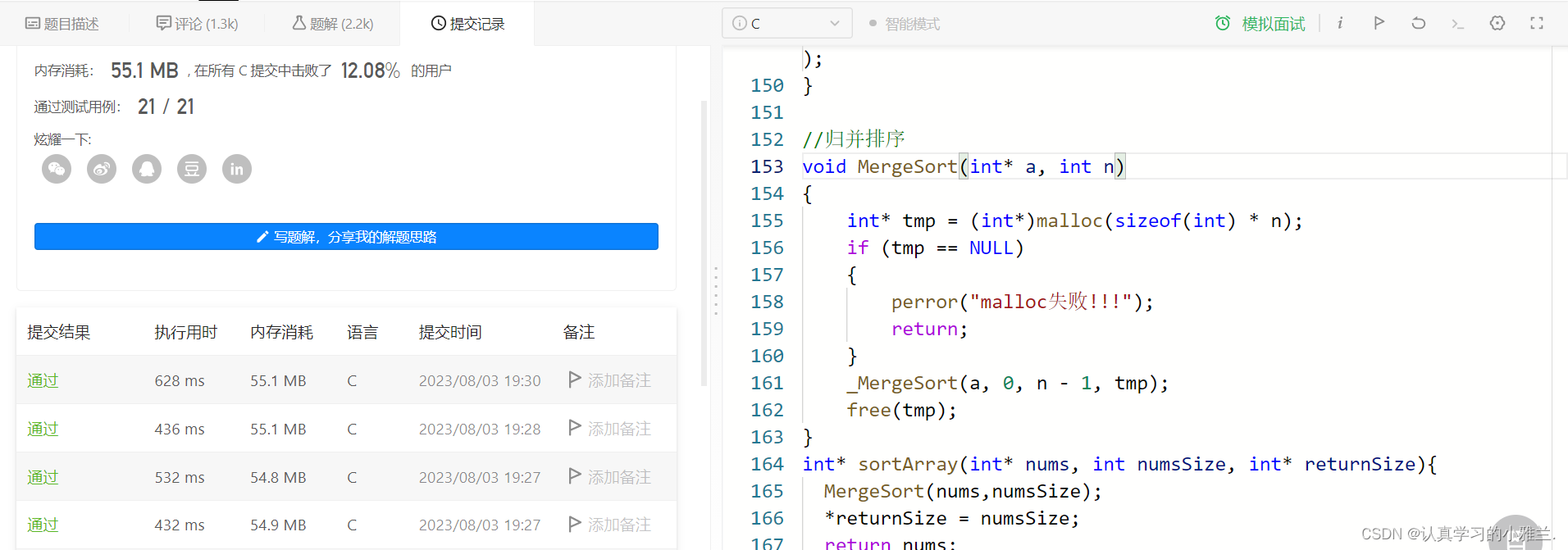
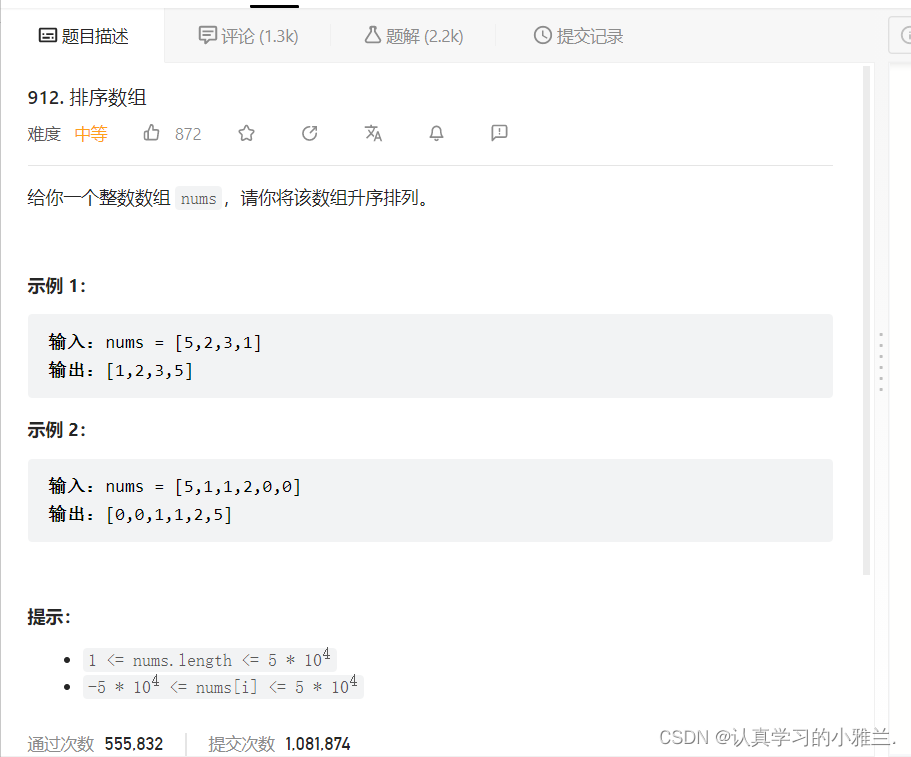
Leetcode每日一题——“912.排序数组”
在leetcode上面有一道题,可以用各种排序测试可不可以通过:
小雅兰在这边尝试了一下归并排序,很轻松就过啦!!!
void _MergeSort(int* a, int begin, int end, int* tmp) {if (begin >= end){return;}int mid = (begin + end) / 2;//[begin,mid] [mid+1,end]_MergeSort(a, begin, mid, tmp);_MergeSort(a, mid + 1, end, tmp);//归并两个区间int begin1 = begin;int begin2 = mid + 1;int end1 = mid;int end2 = end;int i = begin;while (begin1 <= end1 && begin2 <= end2){if (a[begin1] < a[begin2]){tmp[i++] = a[begin1++];}else{tmp[i++] = a[begin2++];}}while (begin1 <= end1){tmp[i++] = a[begin1++];}while (begin2 <= end2){tmp[i++] = a[begin2++];}memcpy(a + begin, tmp + begin, sizeof(int) * (end - begin + 1)); } //归并排序 void MergeSort(int* a, int n) {int* tmp = (int*)malloc(sizeof(int) * n);if (tmp == NULL){perror("malloc失败!!!");return;}_MergeSort(a, 0, n - 1, tmp);free(tmp); } int* sortArray(int* nums, int numsSize, int* returnSize){MergeSort(nums, numsSize);*returnSize = numsSize;return nums; }
还可以这样写,是进行了小区间优化的版本,相对来说好一点,但leetcode上面测试不了此效果:
//直接插入排序 void InsertSort(int* a, int n) {int i = 0;for (i = 1; i < n; i++){int end = i - 1;int tmp = a[i];while (end >= 0){//插入的数据比原来的数据小if (a[end] > tmp){a[end + 1] = a[end];--end;}else{break;}}a[end + 1] = tmp;} } void _MergeSort(int* a, int begin, int end, int* tmp) {if (begin >= end){return;}//小区间优化if(end-begin+1<10){InsertSort(a+begin,end-begin+1);return;}int mid = (begin + end) / 2;//[begin,mid] [mid+1,end]_MergeSort(a, begin, mid, tmp);_MergeSort(a, mid + 1, end, tmp);//归并两个区间int begin1 = begin;int begin2 = mid + 1;int end1 = mid;int end2 = end;int i = begin;while (begin1 <= end1 && begin2 <= end2){if (a[begin1] < a[begin2]){tmp[i++] = a[begin1++];}else{tmp[i++] = a[begin2++];}}while (begin1 <= end1){tmp[i++] = a[begin1++];}while (begin2 <= end2){tmp[i++] = a[begin2++];}memcpy(a + begin, tmp + begin, sizeof(int) * (end - begin + 1)); }//归并排序 void MergeSort(int* a, int n) {int* tmp = (int*)malloc(sizeof(int) * n);if (tmp == NULL){perror("malloc失败!!!");return;}_MergeSort(a, 0, n - 1, tmp);free(tmp); } int* sortArray(int* nums, int numsSize, int* returnSize){MergeSort(nums,numsSize);*returnSize = numsSize;return nums; }
但是这道题,用直接插入排序、冒泡排序这种排序就过不了了,会提示:超出时间限制
遗憾的是:快速排序也没过,小雅兰反复测试了好多遍
好啦,小雅兰今天的归并排序的内容就到这里啦,还要继续加油!!!