文章目录
- 前言
- 🌟一、练习一下
- 🌏1.例一
- 🌏2.例二
- 🌏3.例三
- 🌏4.例四
- 🌟二、浮点型在内存中的储存
- 🌏1.浮点数
- 🌏2.浮点数存储
- 💫(1).二进制浮点数
- 💫(2).浮点数的存储规定
- 💫(3).浮点数的取出规定
- 🌏3.例题
- 😽总结
前言
👧个人主页:@小沈熬夜秃头中୧⍤⃝❅
😚小编介绍:欢迎来到我的乱七八糟小星球🌝
📋专栏:C语言学习
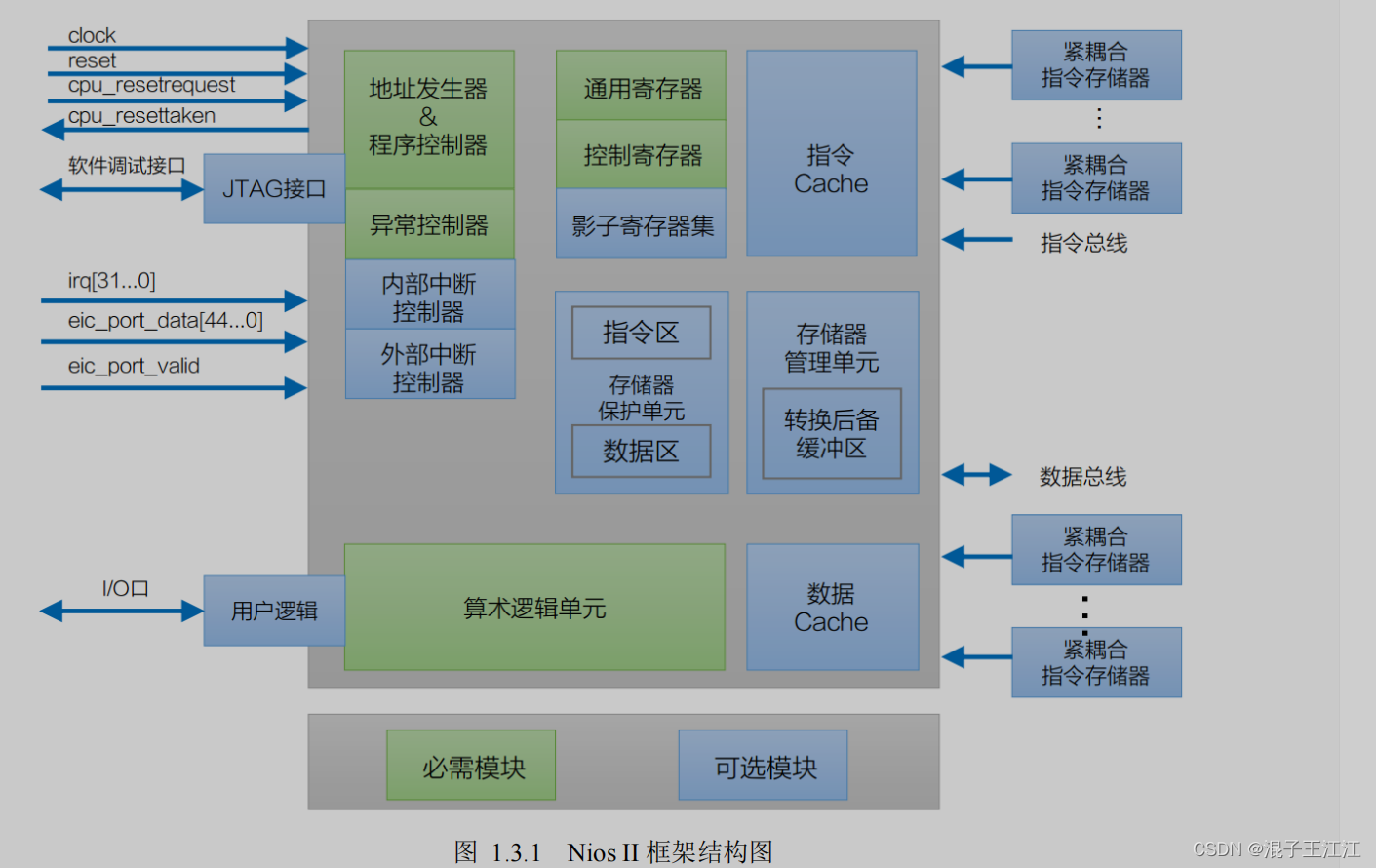
🔑本章内容:C-数据的储存(下)
送给各位💌:学无止境
记得 评论📝 +点赞👍 +收藏😽 +关注💞哦~
🌟一、练习一下
🌏1.例一
看过C语言学习第十五弹后我们一起来做一下下面这道例一
#include<stdio.h>
#include<windows.h>
int main()
{unsigned int i;for (i = 9; i >= 0; i--){printf("%u\n", i);Sleep(1000);//单位毫秒}return 0;
}
答案:死循环
解析:因为这是一个无符号int 类型的i所以当i=0再- -时,成为-1,但是无符号整形中没有符号位所以就变成了一个很大的数一直打印这个条件恒成立,所以就死循环了

🌏2.例二
看过例一我们来做一下例二:
#include<stdio.h>
#include<windows.h>
int main()
{unsigned int i;for (i = 9; i >= 0; i--){printf("%d\n", i);Sleep(1000);//单位毫秒}return 0;
}
答案:死循环
解析:虽然这是一个无符号整形i,但是打印的时候用的%d(打印有符号整形的),所以它是由符号位的,但有人可能要问了-1不就不满足i>=0吗?别忘了i是一个我无符号整型只不过打印用的%d但这并不影响i是一个无符号整型所以判断的时候i>=0是根据无符号数判断的

🌏3.例三
#include<stdio.h>
int main()
{char a[1000];int i;for (i = 0; i < 1000; i++){a[i] = -1 - i;}printf("%d", strlen(a));return 0;
}
答案:255
解析:经过循环a[i]里面存的是-1 -2 -3…-127 -128但是char 类型所以不存在-129 -130…-1000,-128减去1,就变成了127 依次往后127 126 125…3 2 1 0,这才是256个数字了,所以接着循环3 2 1 0…-128 -127-126…127 …3 2 1 0直到数组填满但是strlen是求字符串的长度,找的是\0,\0的ASCII码值是0所以到第一次为0的时候就找到了长度是255.


🌏4.例四
#include<stdio.h>
unsigned char i = 0;
int main()
{for (i = 0; i <= 255; i++){printf("hello world\n");}return 0;
}
答案:死循环
解析:
因为无符号char的范围是0~255;所以当i=255是再++不会变成256因为会发生截断再次变成0由此造成死循环。下面是256的二进制位可以看到截断后二进制是00000000所以不会出现266,条件恒成立。


🌟二、浮点型在内存中的储存
🌏1.浮点数
浮点数的家族包括:float, double ,long double
浮点数表示范围:float.h中定义
🌏2.浮点数存储
💫(1).二进制浮点数
根据国际标准IEEE(电气和电子工程协会)754,任意一个二进制浮点数v可以表示成下面的形式:
(1). (-1)^S* M* 2^E
(2).(-1)^S表示符号位,当S=0,V为正数;当S1,为负数。M表示有效数字,大于等于1,小于2’。
(3).2^E表示指数位。
v = (-1)^ s * 2^E * M
举例来说:根据上述公式,5.5 怎么写呢?
解析:1111.1111,我们都知道二进制位每位都有权重,小数点前面的1权重是0依次往前就是0 1 2 3…;小数点后面的权重则是-1依次往后-1 -2 -3…;所以5.5的二进制可以写成101.1,小数点往前移可以写成1.011*2^2,前面的第一个2代表二进制而第二个2代表移动了两位;加上正负号,因为5.5是正数所以S=0,最终可以写成V=(-1) ^ 0 * 2 ^2 1.011.所以S=0;M=1.011;E=2
举例来说:那么5.0和-5.0怎么写呢?
解析:十进制的5.0,写成二进制是101.0,相当于1.01×2^2。那么,按照上面V的格式,可以得出S=0,M=1.01,E=2。
十进制的-5.0,写成二进制是-101.0,相当于-1.01x2^2。那么,S=1,M=1.01,E=2。
举例来说:那么5.3怎写呢?
解析:十进制的5.3 写成二进制是不能精准由后面的数凑出来所以说不能精准保存
举例来说:那么0.5怎么写呢?
十进制的0.5,写成二进制是0.1(小数点后的第一位权重是-1所以相当于2^(-1)),也就是0.5,相当于1.0*2 ^(-1)。那么,按照上面V的格式,可以得出S=0,M=1.0,E=-1。
💫(2).浮点数的存储规定
IEEE 754对有效数字M和指数E,还有一些特别规定。
前面说过,1<M<2,也就是说,M可以写成1.xxxxxx的形式,其中xxxxxx表示小数部分。IEEE 754规定,在计算机内部保存M时,默认这个数的第一位总是1,因此可以被舍去,只保存后面的xxxxxx部分。比如保存1.01的时候,只保存01,等到读取的时候,再把第一位的1加上去。这样做的目的,是节省1位有效数字。以32位浮点数为例,留给M只有23位,将第一位的1舍去以后,等于可以保存24位有效数字。
至于指数E,情况就比较复杂。
首先,E为一个无符号整数(unsigned int)这意味着,如果E为8位,它的取值范围为O~255;如果E为11位,它的取值范围为0-2047。但是,我们知道,科学计数法中的E是可以出现负数的,所以IEEE754规定,存入内存时E的真实值必须再加上一个中间数,对于8位的E,这个中间数是127;对于11位的E,这个中间数是1023。比如,2^10的E是10,所以保存成32位浮点数时,必须保存成10+127=137,即10001001。
float 32位的浮点型
double 64位的浮点型

也就是:例如5.5的存法
二进制:101.1
(-1)^ 01.011 * 2^2根据规定float类型E+127就变成了129;129的二进制序列10000001(E);M存的小数点后面的也就是(01100000000000000000000)再加上S中存储的0就变成了01000000101100000000000000000000转换成十六进制(四个二进制转换成一个十六进制位4 0 b 0 0 0 0 0

💫(3).浮点数的取出规定
然后,指数E从内存中取出还可以再分成三种情况:
(1).E不全为0或不全为1
这时,浮点数就采用下面的规则表示,即指数E的计算值减去127(或1023),有效数字M前加上第一位的1。
比如:
0.5 (1/2)的二进制形式为0.1,由于规定正数部分必须为1,即将小数点右移1位,则为1.0*2N(-1),其阶码为-1+127=126,表示为01111110,而尾数1.0去掉整数部分为0,补齐0到23位00000000000000000000000,则其二进制表示形式为:0 01111110 00000000000000000000000
(2).E全为0
这时,浮点数的指数E等于1-127(或者1-1023)即为真实值,有效数字M不再加上第一位的1,而是还原为0.xxxxxx的小数。这样做是为了表示(±)0,以及接近于0的很小的数字。
(3).E全为1
这时,如果有效数字M全为0,表示±无穷大(正负取决于符号位s);
🌏3.例题

解析:
以整数的视角,存放整型的数字
00000000000000000000000000001001-9的原反补相同;9(%d打印整形)
浮点数存储:
0(S) 00000000(E) 0000000000000000001001(M);E为全0,浮点数的指数E等于1-127(或者1-1023)即为真实值;E=1-127=-126;有效数字M不再加上第一位的1,而是还原为0.xxxxxx的小数M=0.0000000000000000001001
(-1)^ 0 * 0.00000000000000000010012^(-126)所以浮点数打印出来是0.000000
以浮点数的视角,存放浮点型的数字
二进制:1001.0
1.0012^3
(-1)^ 0 * 1.001 * 2^3
S=0;E=3;M=1.001*
01000001000100000000000000000000-正数原码反码补码相同%d打印出来是1091567616
😽总结
😽Ending,今天的C—数据的储存(下)内容就到此结束啦~,如果后续想了解更多,就请关注我吧,一键三连哦 ~