1.
#seaborn绘制常用图表
#折线图
#replot(x,y,kind,data)
#lineplot(x,y,data)
#直方图
#displot(data,rug)
#条形图
#barplot(x,y,data)
#散点图
#replot(x,y,data)2.

#绘制折线图第一种方式
sns.set_style('darkgrid')#设置风格样式
df=pd.read_excel('成绩表.xlsx')
sns.relplot(x='姓名',y='数学',kind='line',data=df)
plt.xticks(df['姓名'],rotation=90)
plt.show()#绘制折线图第二种方式
sns.set_style('darkgrid')#设置风格样式
df=pd.read_excel('成绩表.xlsx')
sns.lineplot(x='姓名',y='数学',data=df)
plt.xticks(df['姓名'],rotation=45)
plt.show()#绘制多折线图
df=pd.read_excel('成绩表.xlsx')
df1=df[['数学','语文','英语']]
dfs=[df1['数学'],df1['语文'],df1['英语']]
sns.lineplot(data=dfs)
plt.show()3.
#绘制直方图
df=pd.read_excel('data2.xlsx')
data=df[['得分']]
sns.distplot(data,rug=True)
plt.show()#绘制条形图
df=pd.read_excel('成绩表.xlsx')
sns.barplot(x='姓名',y='数学',data=df)
plt.show()#绘制散点图
#读取数据
df=sns.load_dataset('tips')#seaborn自带的数据集
sns.relplot(x='total_bill',y='tip',data=df,color='r')
plt.show()4.

#seaborn绘制常用图表
#绘制线性回归模型
#Implot(x,y,data)
#箱型图
#boxplot(data,rug)
#绘制核密度图
#kdeplot(data,shade=True)
#绘制边际核密度图
#jointplot(x,y,kind,space)
#绘制提琴图
#violinplot(x,y,hue,data)#线性回归
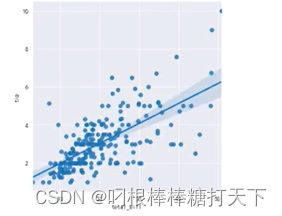
sns.set_style('darkgrid')
df=sns.load_dataset('tips')#自带数据集
sns.Implot(x='total_bill',y='tip',data=df)
plt.show()
#箱型图
sns.set_style('darkgrid')
df=sns.load_dataset('tips')#自带数据集
sns.boxplot(x='day',y='total_bill',hue='time',data=df)
plt.show()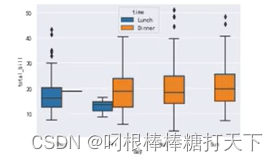
#核密度图
sns.set_style('darkgrid')
df=sns.load_dataset('iris')#自带数据集
sns.kdeplot(df['petal_width'],shade=True,color='r')
sns.kdeplot(df['petal_length'],shade=True,color='b')
plt.show()

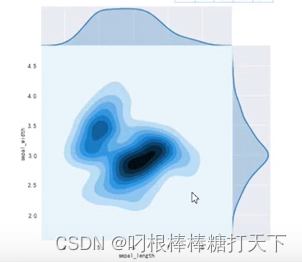
#编辑核密度图
sns.set_style('darkgrid')
df=sns.load_dataset('iris')#自带数据集
sns.jointplot(x=df['speal_length'],y=df['speal_width'],kind='kde',space=0)
plt.show()
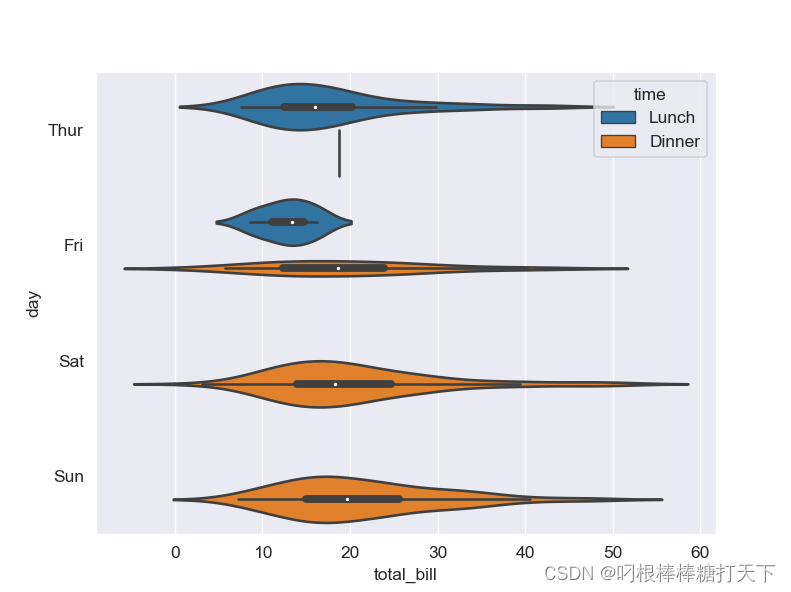
#提琴图
sns.set_style('darkgrid')
df=sns.load_dataset('tips')#自带数据集
sns.violinplot(x='total_bill',y='day',hue='time',data=df)
plt.show()