---

一、单值二叉树

单值二叉树

如果二叉树每个节点都具有相同的值，那么该二叉树就是单值二叉树。只有给定的树是单值二叉树时，才返回 true；否则返回 false。

需要保证全部都相等，自然就需要左右子树都没问题。先想一个小问题，当遍历一个子树时，最终会遇到空，遇到空就要返回true，让它安全返回，不影响判断，这里也就说我们需要递归来遍历。那么现在从根开始，首先有一个判断，如果是空就返回true，跳过这个判断后，如果进行下一步？我们要让根和其他所有数字都相等，这其中最容易判断的就是根的左右子树是否相等，所以可能会写出这一个判断语句

if(root->val != root->right->val)

这个语句还欠缺考虑。要知道，现在我们的思路是用一个根节点去和它的两个子树比较是否相等，前提是两个子树都存在。前面的判断空是在判断root，也就是判断这个根节点，并没有判断它的子树们，所以应该这样写：if(root->right && root->right->val) 。如果符合条件了，那么这就不是单值二叉树，就得返回false了，返回的false也必须让之前的递归全部都false，最终才是false。

先不想这个，回到刚才的代码，我们只写了右边，还需要写左边，也是一样，也就是两个if，都需要判断。写完这三个判断后，就得递归了。前面说到false得让整体，所有的递归都为false，并且从题目中也知道，左右子树节点的值都得等于根才行，所以当往下继续遍历的时候，需要用&&来连接

return isUnivalTree(root->left) && isUnivalTree(root->right);

整体的代码

bool isUnivalTree(struct TreeNode* root) 
{if(!root) return true;if(root->left && root->val != root->left->val)return false;if(root->right && root->val != root->right->val)return false;return isUnivalTree(root->left) && isUnivalTree(root->right);
}

这道题也就结束了。题解中还有一种写法，是在判断左和右是否相等时进入递归，但这样不妥，如果从根开始，它的右子树节点的值就不相等，而程序在前面判断左子树时，如果相等，就开始了继续找左子树的递归，那么就白白浪费空间和时间了，所以现在现有的左右子树判断完再递归更好。

二、检查两颗树是否相同

相同的树

给你两棵二叉树的根节点 p 和 q ，编写一个函数来检验这两棵树是否相同。如果两个树在结构上相同，并且节点具有相同的值，则认为它们是相同的。

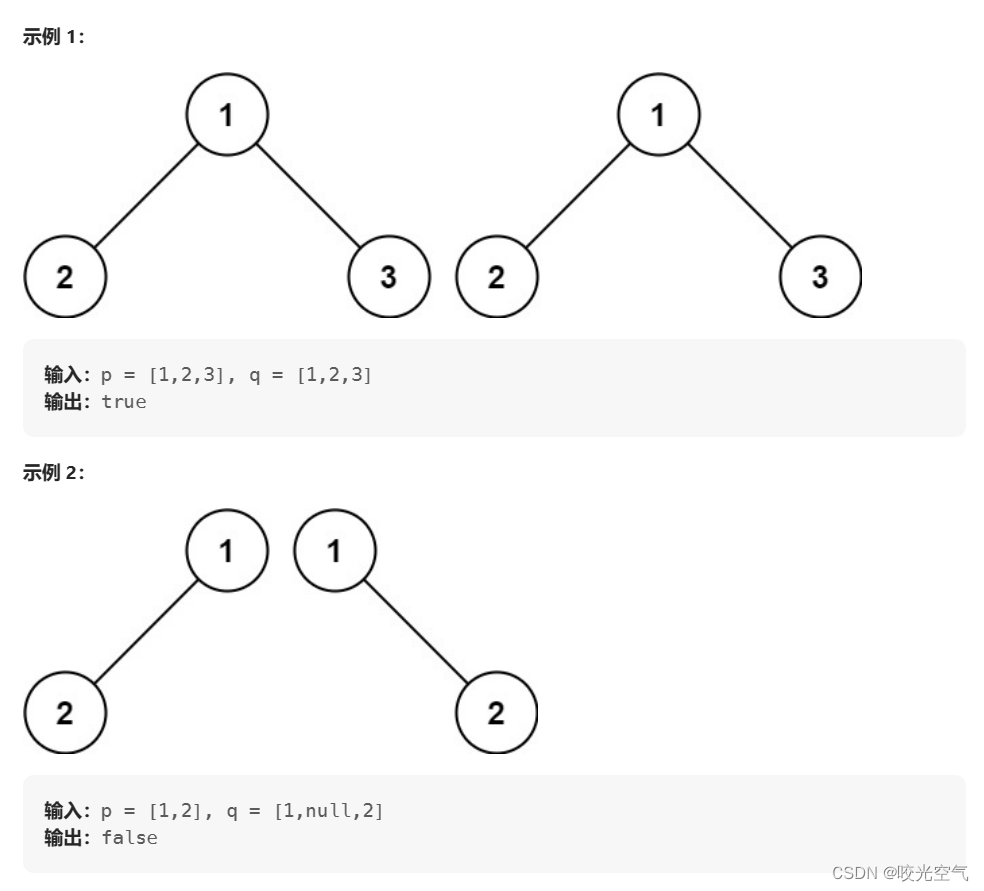
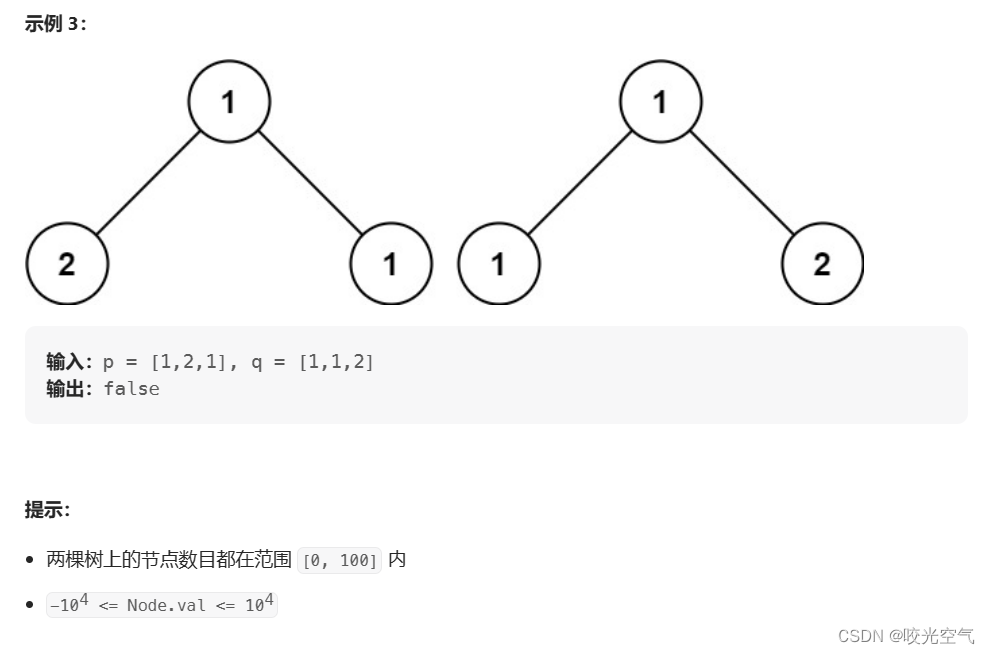
两棵树比较，值要相等，结构要相同。从根开始，如果两个值相等，这肯定符合要求，但是这时候不能返回true，我们还要继续往下判断，让递归进行下去，去看子树的情况，判断结构是否相同，但是不相等肯定就不行，就不是相同的树，所以可以写如果值不相等，就返回false。要让程序能够持续到最低层，来判断整体的结构是否相同，就得让其他判断条件也不能阻碍递归的前进，直到我们来到空，比如上面的例一中，2的左子树，这时候为空，如果另一棵树此时也是空，那就没问题，返回true，再往回走，去判断它的父节点的右子树；如果一个为空，一个不为空，那肯定不行，就直接返回false。而这里有一个巧妙的写法，先写两个都是空的判断，如果不是，那就要么是一空一不空，要么两个都不空，那就可以写if(p == NULL || q == NULL) 有一个为空就说明结构不相同了，因为是一空一不空。

上面这段已经写了三个判断，这三个判断就足以完成题目的要求，在最后加一个左右子树的递归即可。

bool isSameTree(struct TreeNode* p, struct TreeNode* q){if(p == NULL && q == NULL) return true;if(p == NULL || q == NULL) return false;if (p->val != q->val) return false;return isSameTree(p->left, q->left) && isSameTree(p->right, q->right);
}

三、另一棵树的子树

另一棵树的子树

给你两棵二叉树 root 和 subRoot 。检验 root 中是否包含和 subRoot 具有相同结构和节点值的子树。如果存在，返回 true ；否则，返回 false 。二叉树 tree 的一棵子树包括 tree 的某个节点和这个节点的所有后代节点。tree 也可以看做它自身的一棵子树。

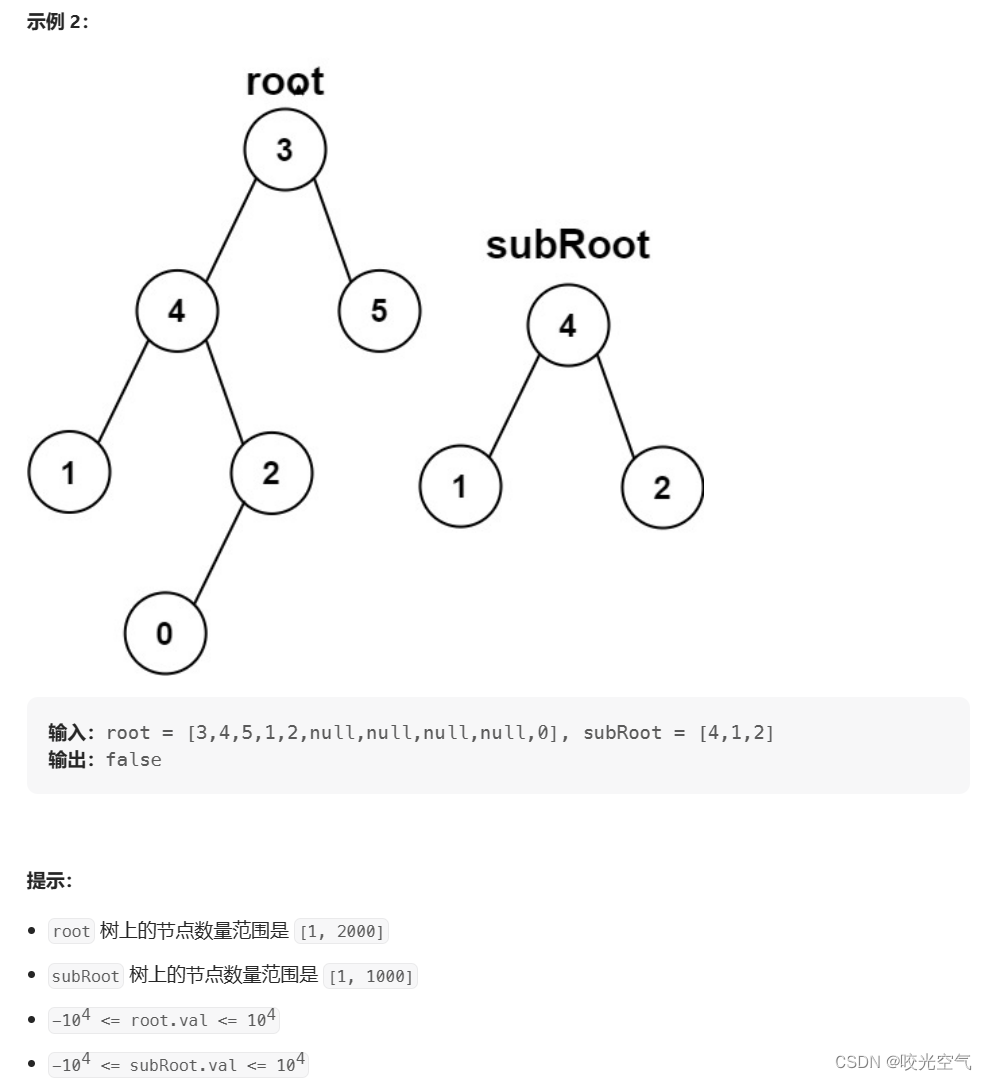
既然要找子树，也就是要找到root中subRoot相同的一部分，这里就能用到刚才写的isSameTree。root有很多个子树，我们只能一个个比较，看看是否和subRoot相同，从根开始，整棵树也是root的子树，所以从root开始比较，如果root和subRoot是相同的树，那么就返回true。如果一次比较，发现不相同，程序得继续往下寻找，像例2那样，2下面还有一个0，那么从4开始比较，下面的部分就不相同，不相同，什么也不返回，继续找4的左子树和右子树进行比较。这里会想到我们要写两个式子，一个参数中有root->left，另一个是root->right，这两个只要有一个是true就说明是子树，那么程序就可以结束了，所有用或。一直往下比较，什么时候停止？如果一条路线到了空，说明这一路上的节点下的树都不和subRoot相同，那就说明这条路都不符合条件，那就返回false，返回false也不要紧，因为之前已经写了或，所以程序还会判断另一条路线是否可行，才会给出最终结果。

bool isSameTree(struct TreeNode* p, struct TreeNode* q) {if(p == NULL && q == NULL) return true;if(p == NULL || q == NULL) return false;if(p->val != q->val) return false;return isSameTree(p->left, q->left) && isSameTree(p->right, q->right);
}bool isSubtree(struct TreeNode* root, struct TreeNode* subRoot) {if(!root) return false;if(isSameTree(root, subRoot)) return true;return isSubtree(root->left, subRoot) || isSubtree(root->right, subRoot);
}

四、二叉树的前序遍历

前序遍历

给你二叉树的根节点 root ，返回它节点值的 前序 遍历。

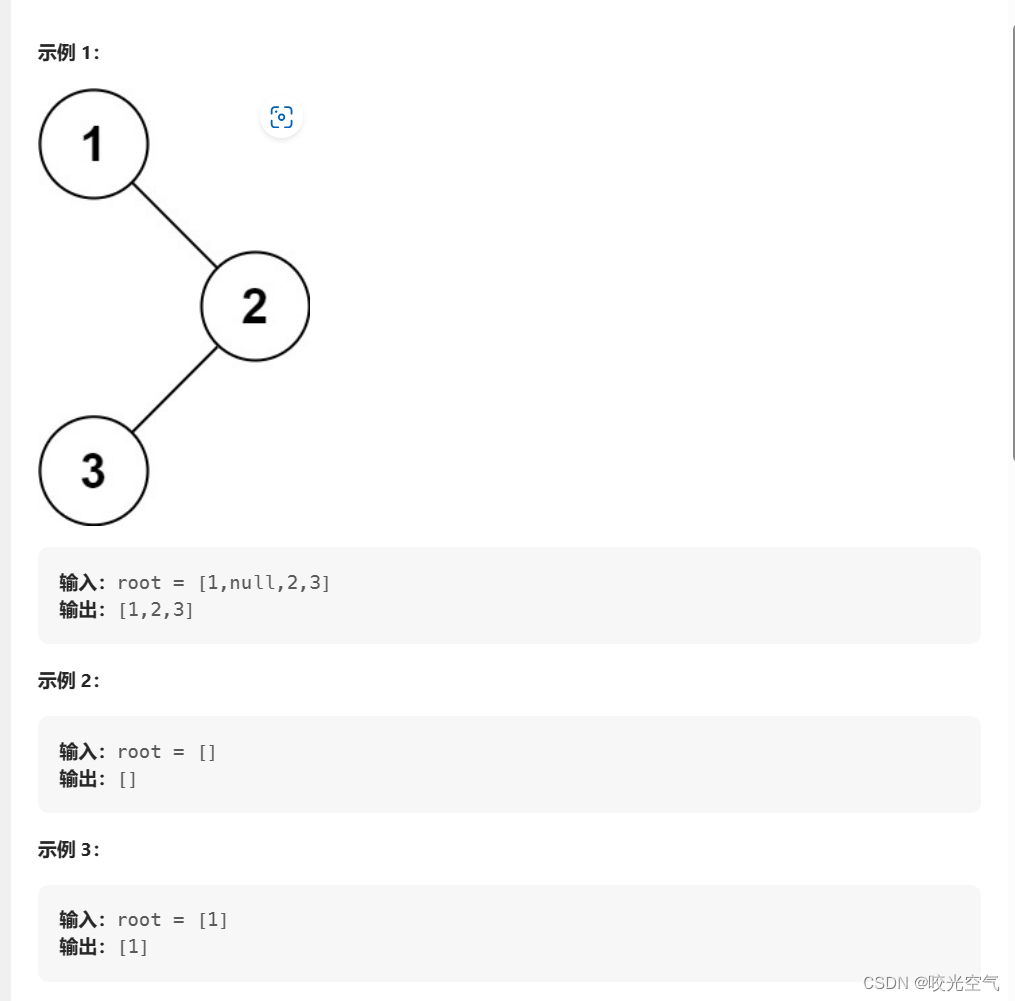
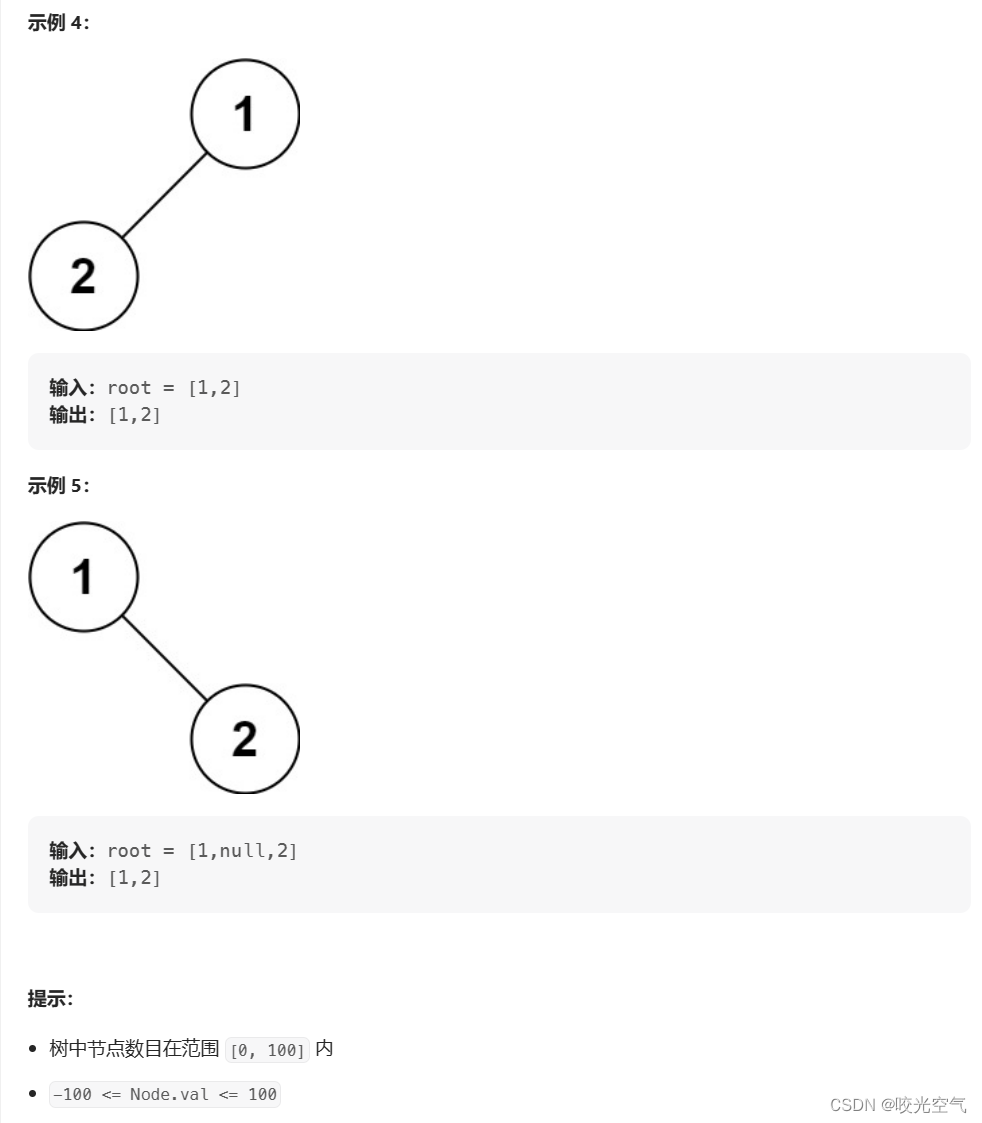
用递归算法解。前序遍历是比较简单的，不过这里要求把遍历的结果放到一个数组中，*returnSize是数组大小，最后返回数组。虽然提示中给了节点数目范围，但用一个函数来计算给的二叉树的节点数目更适合所有树。

int TreeSize(struct TreeNode* root)
{if root == NULL ? 0 : TreeSize(root->left) + TreeSize(root->right) + 1;
}void preorder(struct TreeNode* root, int* array, int* i)
{if(root == NULL){return;}array[(*i)++] = root->val;preorder(root->left, array, i);preorder(root->right, array, i);
}int* preorderTraversal(struct TreeNode* root, int* returnSize){*returnSize = TreeSize(root);int* array = (int*)malloc(sizeof(int) * (*returnSize));int i  = 0;preorder(root, array, &i);return array;
}

五、对称二叉树

对称二叉树

给你一个二叉树的根节点 root，检查它是否轴对称。

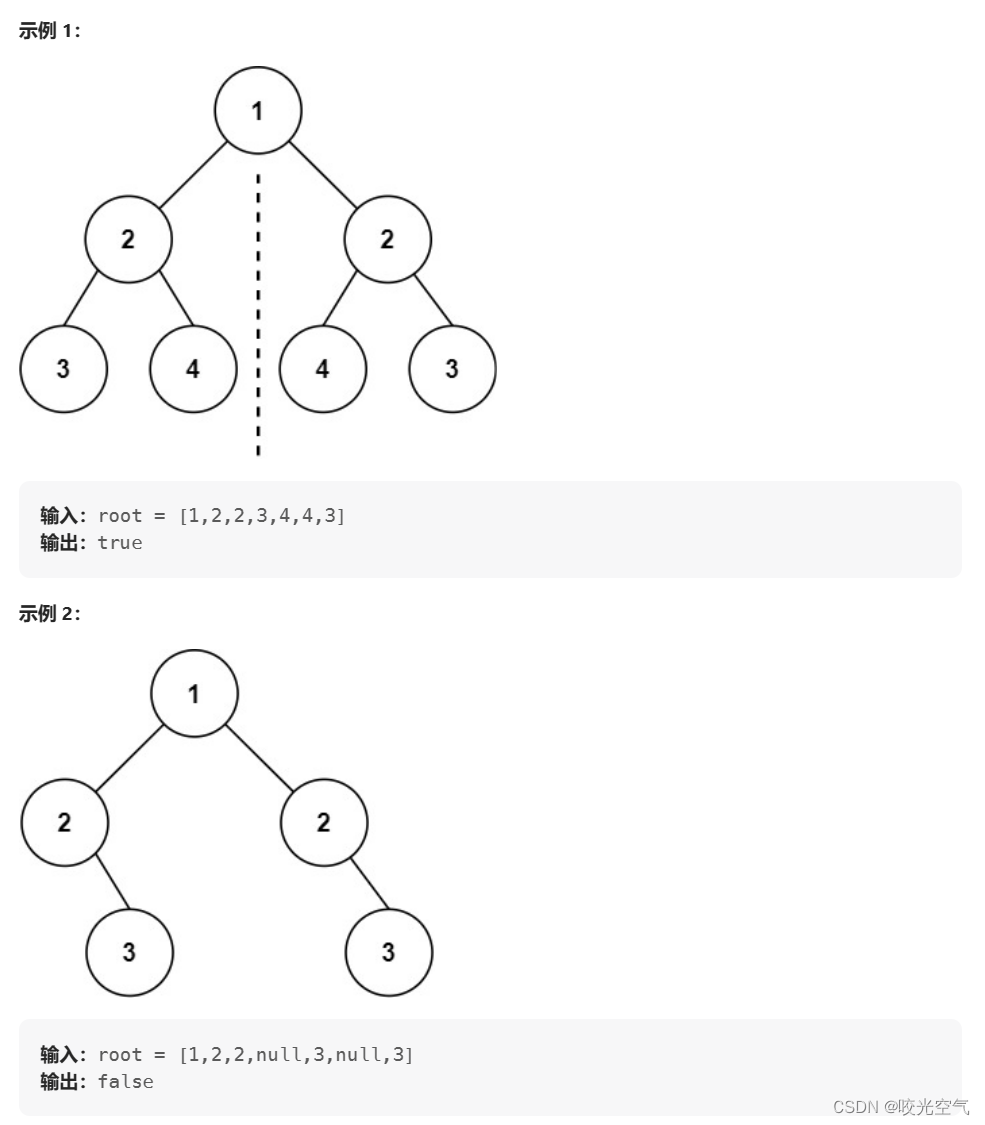
对称二叉树，根的左右子树需要比较，看是否对称，这里能够想到判断相同，不过有一定差别，根节点值同样也要相等，左子树和另一个的右子树比较，右子树和另一个的左子树比较。

另一个思路就是翻转二叉树，把左右子树翻转过来，那么就可以直接比较相同了，翻转不难，大事化小，遍历最低一层的子树，然后逐个翻转，往上走，最后完成翻转。但其实这个思路不行，如果翻转二叉树，那么翻转后原二叉树就不存在了，我们只能复制一份，然后再翻转才行，但是复制又得走一遍递归了，所以这个思路更复杂。

bool isSameTree(struct TreeNode* p, struct TreeNode* q){if(!p && !q){return true;}if((p == NULL || q == NULL) || (p->val != q->val)){return false;}return isSameTree(p->left, q->right) && isSameTree(p->right, q->left);
}bool isSymmetric(struct TreeNode* root){if(root == NULL){return true;}return isSameTree(root->left, root->right);
}

这里把两个return false的语句合并到了一起。

结束。