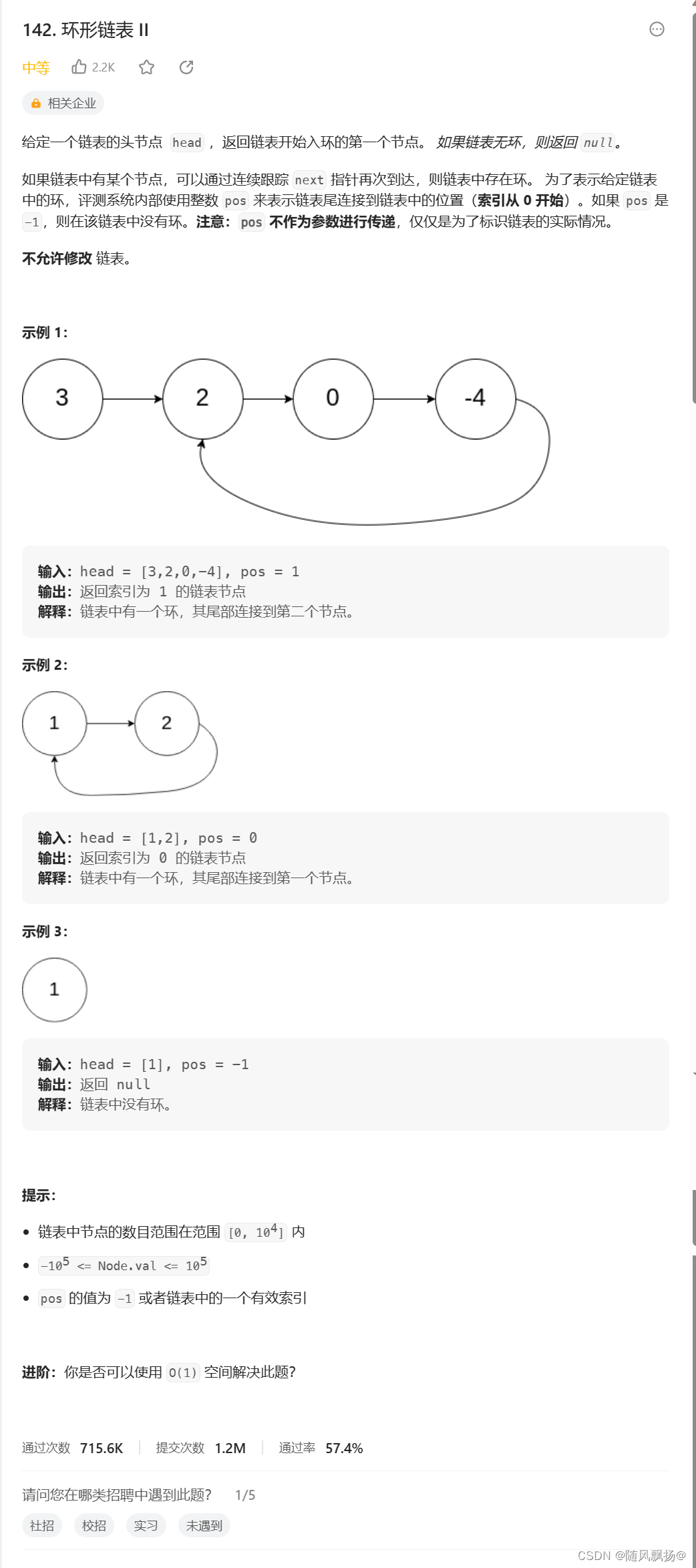
题目链接:
一.环形链表运动基础。
使用快慢指针利用相对移动的思想:
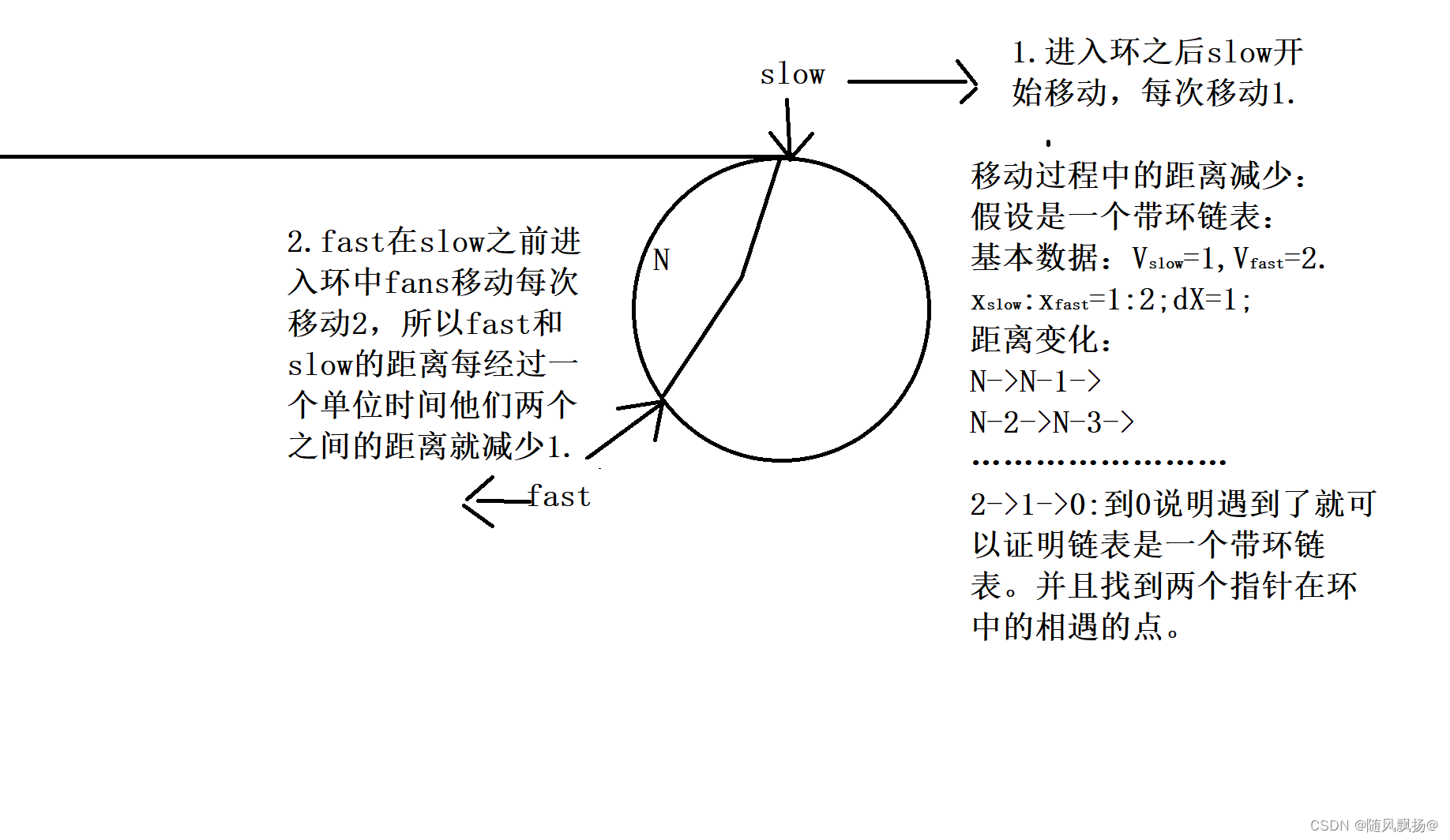
1.第一种情况:
1,令快指针(fast)速度为2.
2.慢指针(slow)速度为1.
3.以慢指针进入环中开始。
4。假设slow刚刚进入环中fast与它相距N。
如图所示:
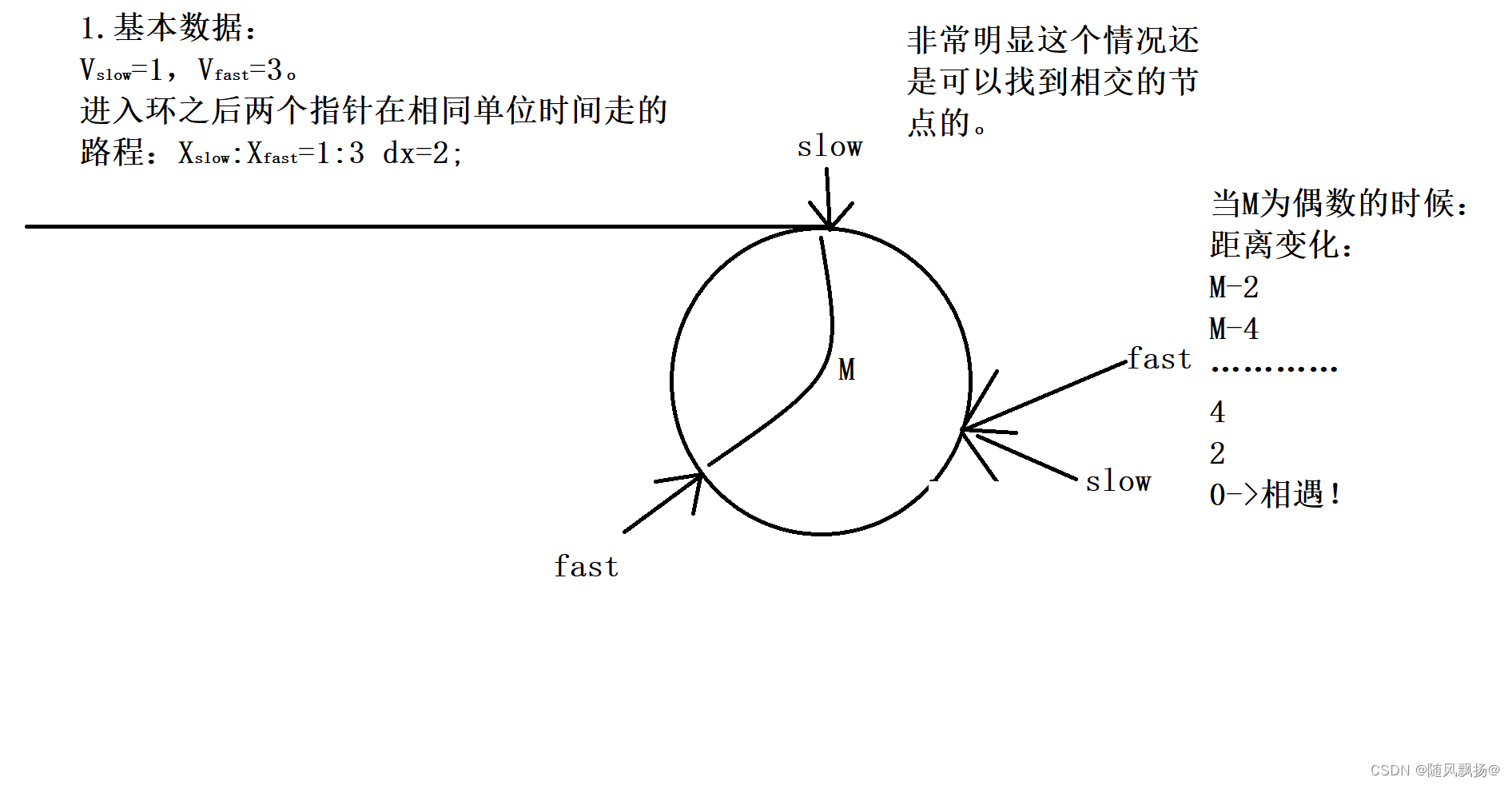
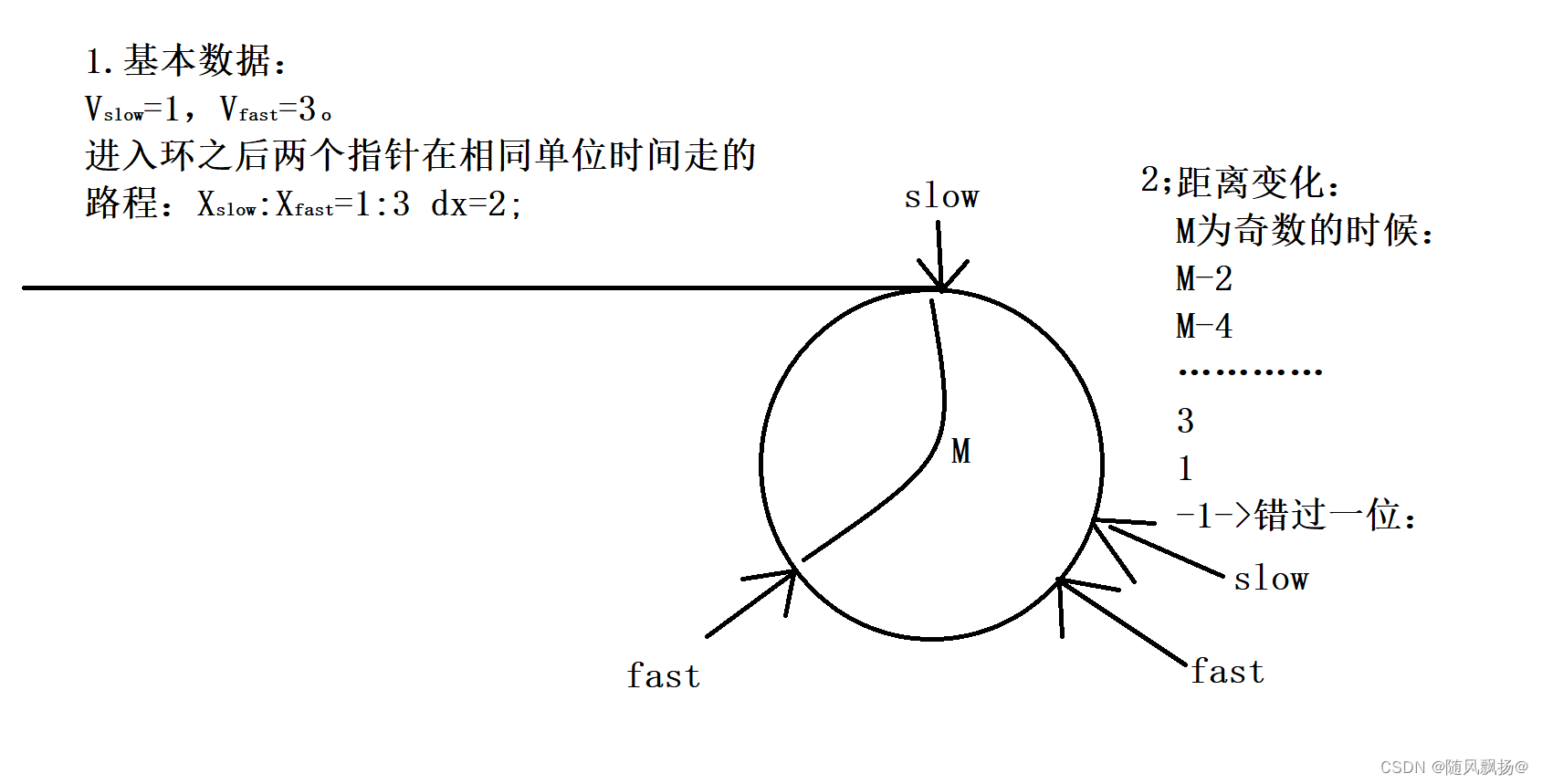
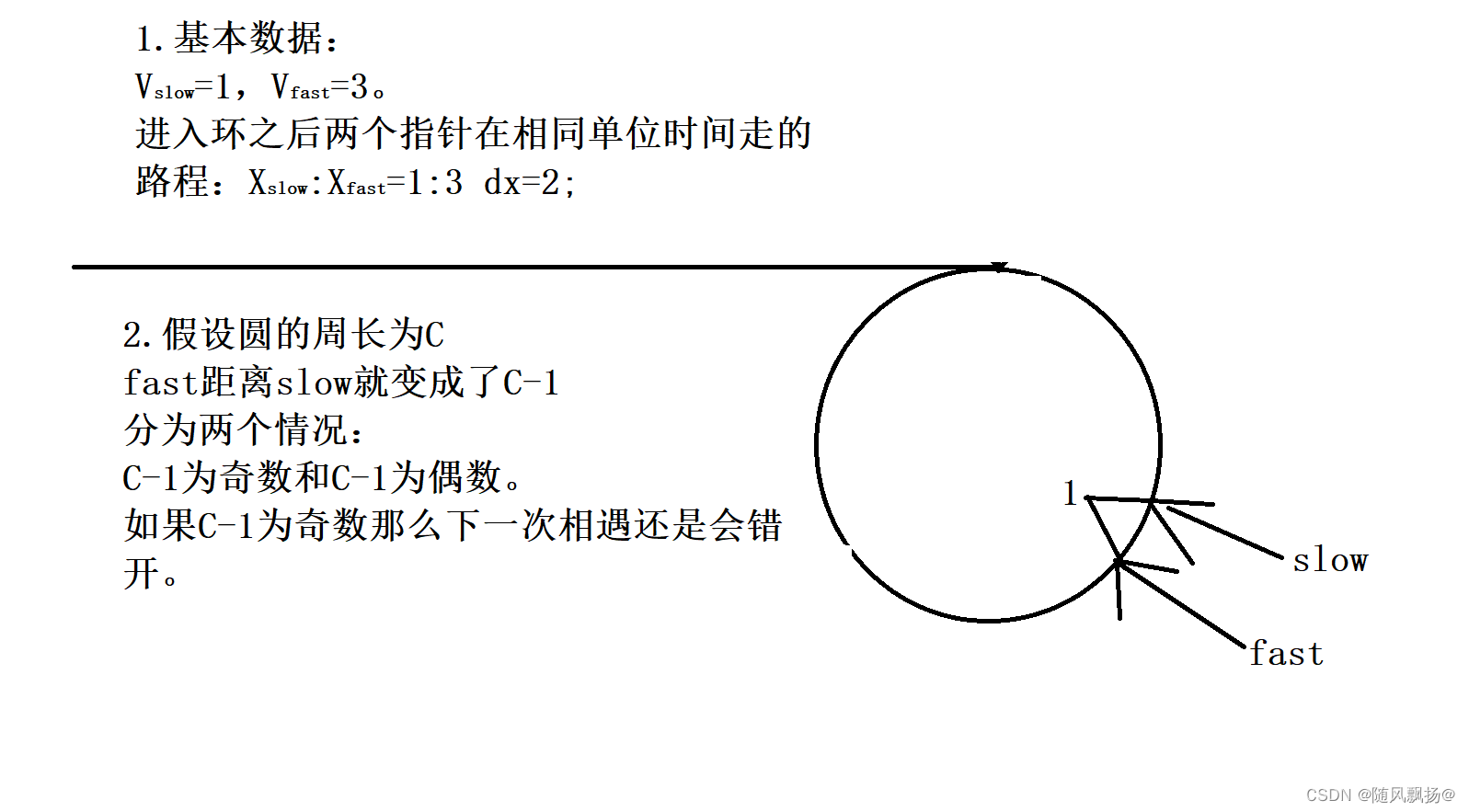
2.第二种情况:
1,令快指针(fast)速度为3.M
2.慢指针(slow)速度为1.
3.以慢指针进入环中开始。
4。假设slow刚刚进入环中fast与它相距M。
如图所示:
3.总结:
我们的距离改变是依靠相对速度而产生的相对距离。当相对速度为1的时候我们只要存在环就一定可以相遇。但是当相对速度为二的时候就相遇考虑之间的距离差值是奇数还是偶数所以判断链表带环的指针速度比较好的是:快指针(fast)速度为2.慢指针(slow)速度为1.
二.带环链表的进入环的节点。
假设:
1.链表无环部分长度:L
2.圆的周长为C
3.慢指针刚刚进入链表是快慢指针的距离为X
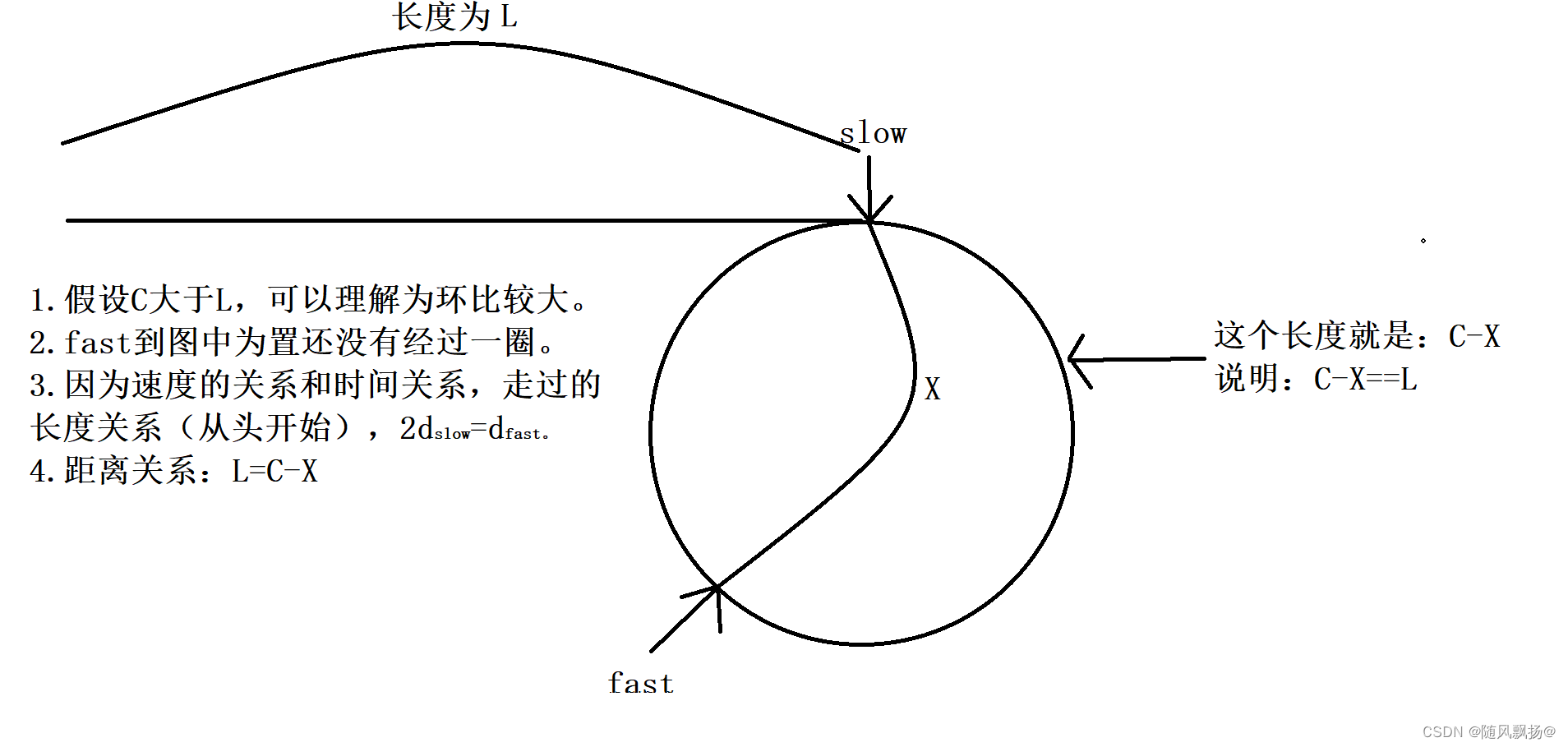
1.第一种情况。
1.当我们的环比较大的情况:
如图所示:
2.第二种情况。
2.当我们的环比较小的时候:
如图所示:
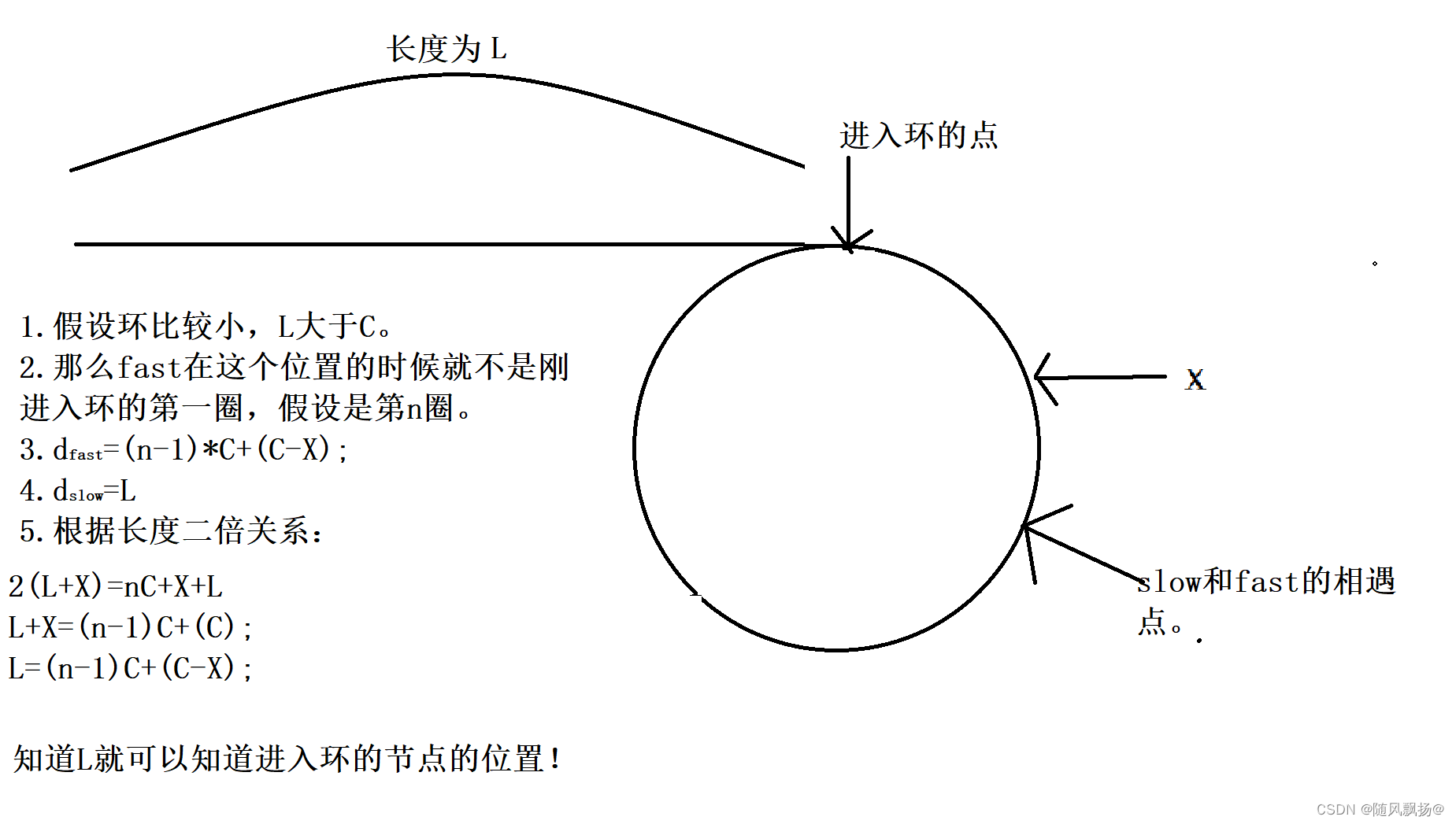
总结:环比较短的推导公式是可以通过n的变化适用于各种情况的。
3.两个思路
思路一:
1.依据我们L=(n-1)C+(C-X)作为理论依据。
2.重新定义两个节点一个从交点开始走每次走一步。
3.一个从头链表头开始走两个节点一定会相遇并且相遇的点就是进入点。
struct ListNode *detectCycle(struct ListNode *head) {struct ListNode* slow=head,*fast=head;//考虑带环还是不带环。while(fast&&fast->next){//进行移动:slow=slow->next;fast=fast->next->next;if(slow==fast){struct ListNode* meet=fast;while(head!=meet){head=head->next;meet=meet->next;} return meet;}}return NULL;}
思路二:
1.假设我们没有理论依据。
2.找到节点之后可以转化成相交链表的问题。
3.找到节点之后把相遇节点的下一个置位空。
4.这样就分开了两个链表链表的位节点就是相遇点。
5.求两个链表的长度进行差距长的先走差距步。
6。一起走相等就是交点。
struct ListNode *getIntersectionNode(struct ListNode *headA, struct ListNode *headB) {struct ListNode* curA=headA,*curB=headB;struct ListNode* tileA=headA,*tileB=headB;int lenA=1,lenB=1;while(tileA->next){tileA=tileA->next;lenA++;}while(tileB->next){tileB=tileB->next;lenB++;}if(tileA!=tileB){//说明没有相交return NULL;}//说明一定相交int gap=abs(lenA-lenB);//2.谁比较大就先走差距步//假设struct ListNode* shortlist=headA,*longlist=headB;if(lenB<lenA){//修正shortlist=headB;longlist=headA;}//长的先走差距补。while(gap--){longlist=longlist->next;}while(shortlist&&longlist){if(shortlist==longlist){return longlist;}else{shortlist=shortlist->next;longlist=longlist->next;}}return NULL;
}
struct ListNode *detectCycle(struct ListNode *head) {struct ListNode* slow=head,*fast=head;//考虑带环还是不带环。while(fast&&fast->next){//进行移动:slow=slow->next;fast=fast->next->next;if(slow==fast){struct ListNode* meet=slow;struct ListNode* new=meet->next;meet->next=NULL;return getIntersectionNode(head,new); }}return NULL;}