目录
- 🍇二叉搜索树概念
- 🍈二叉搜索树查找
- 🍉二叉搜索树的插入
- 🍊二叉搜索树的删除
- 🍍二叉搜索树的查找、插入、删除实现
- 🍋二叉搜索树的应用
- 🥭二叉搜索树的性能分析
- 🍓总结
🍇二叉搜索树概念
二叉搜索树,又称为二叉排序树,是一种特殊的二叉树。它要么是一棵空树,要么具有以下性质:
- 若它的左子树不为空,则左子树上所有节点的值都小于根节点的值;
- 若它的右子树不为空,则右子树上所有节点的值都大于根节点的值;
- 它的左右子树也分别为二叉搜索树。
二叉搜索树的特点是可以快速地查找、插入和删除节点,因为它的节点按照大小关系排列,形成了一种有序结构。它常被用于实现关联数组、集合等数据结构,也是许多其他算法的基础。

🍈二叉搜索树查找
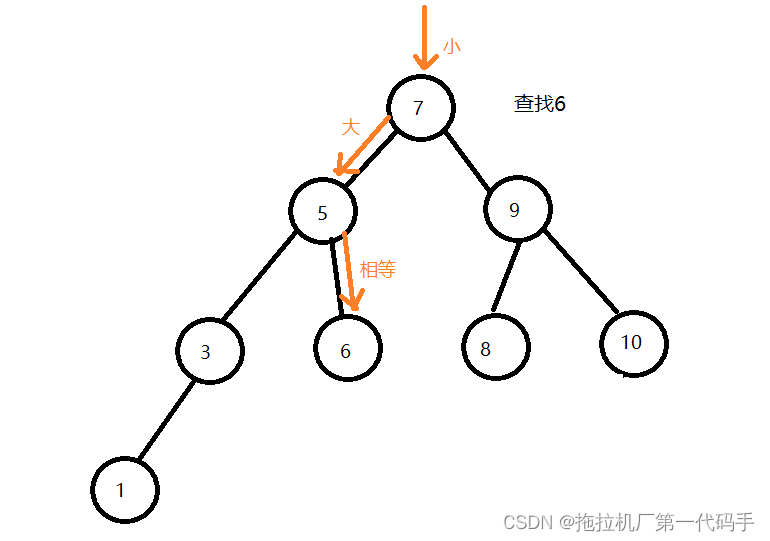
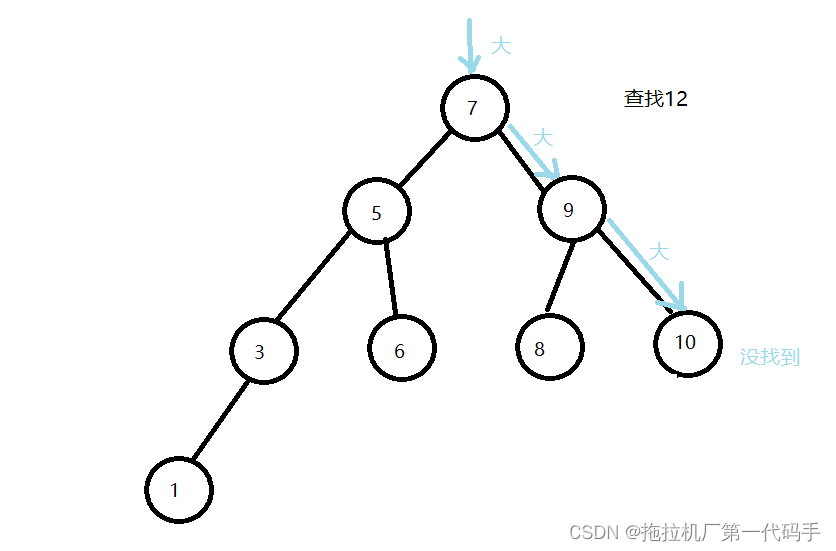
二叉搜索树的查找可以通过以下步骤进行:
-
从根节点开始比较,将待查找的值与根节点的值进行比较,如果相等,则返回该节点;如果待查找的值比根节点的值大,则往右子树走查找,反之则往左子树走查找。
-
重复上述步骤,直到找到待查找的值或者走到空节点仍未找到。如果走到空节点仍未找到,则说明该值不存在于二叉搜索树中。
由于二叉搜索树的节点按照大小关系排列,因此查找的时间复杂度为O(log n),其中n为二叉搜索树中节点的个数。
🍉二叉搜索树的插入
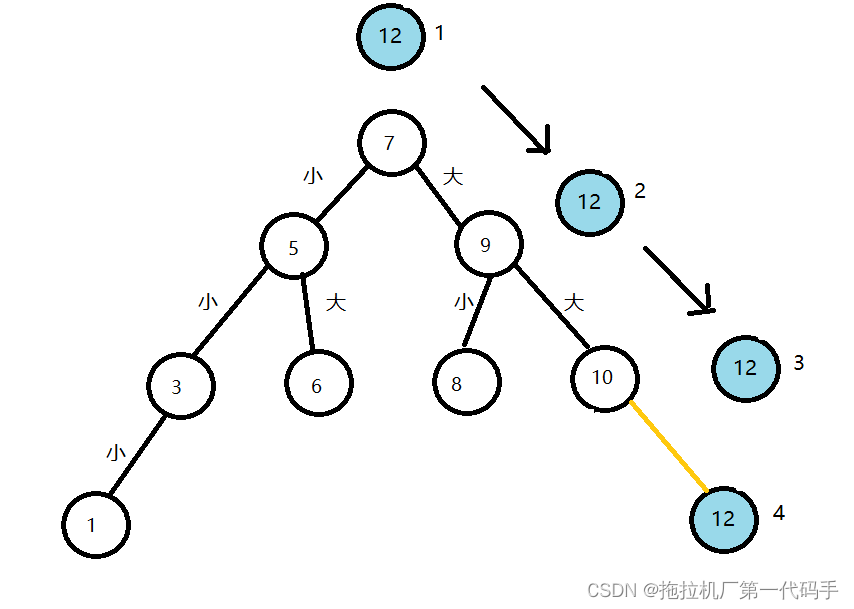
二叉搜索树的插入可以通过以下步骤进行:
-
如果二叉搜索树为空,则直接将新节点作为根节点,赋值给root指针。
-
如果二叉搜索树不为空,则按照二叉搜索树的性质,从根节点开始比较待插入节点的值和当前节点的值的大小关系,如果待插入节点的值比当前节点的值小,则往左子树走查找,如果左子树为空,则将待插入节点作为当前节点的左子节点;
-
如果待插入节点的值比当前节点的值大,则往右子树走查找,如果右子树为空,则将待插入节点作为当前节点的右子节点。
-
如果待插入节点的值与当前节点值相等,表示已经存在这个值,插入失败。
-
重复上述步骤,直到找到合适的插入位置为止。
二叉搜索树的插入时间复杂度为O(log n),其中n为二叉搜索树中节点的个数。
🍊二叉搜索树的删除
二叉搜索树的删除可以通过以下步骤进行:
首先查找待删除的节点是否在二叉搜索树中,如果不存在,则直接返回;否则,进入下一步操作。
根据待删除节点的情况,进行以下处理:
-
如果待删除节点是叶子节点,则直接删除该节点即可。
-
如果待删除节点只有左子树或者右子树,则将待删除节点的父节点指向待删除节点的子节点,然后删除待删除节点。
-
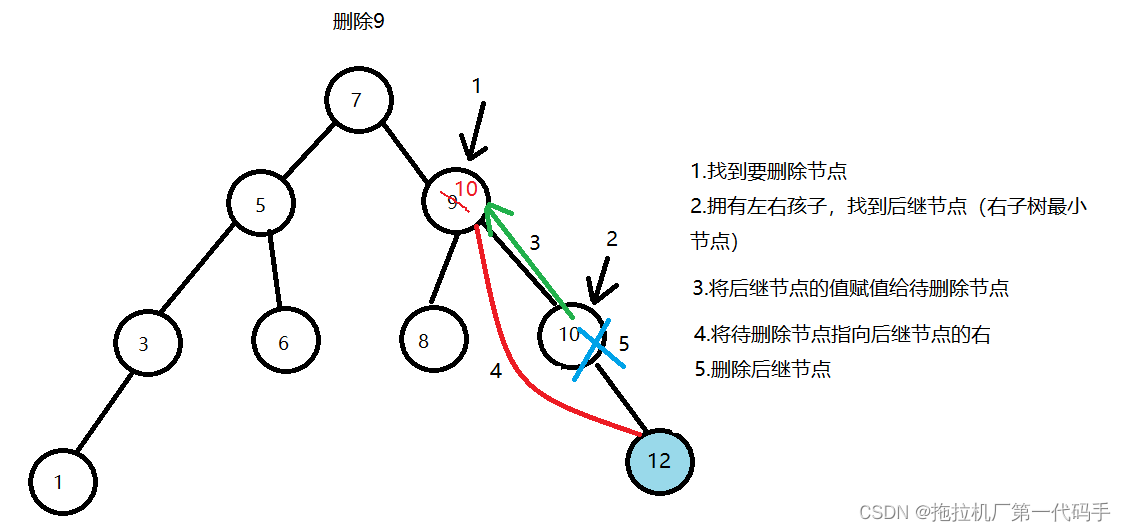
如果待删除节点既有左子树又有右子树,则需要找到它的中序遍历下的后继节点(即右子树中的最小节点),将后继节点的值赋给待删除节点,然后将待删除节点的右指向后继节点的右,然后删除后继节点。
重复上述步骤,直到完成待删除节点的删除。
需要注意的是,二叉搜索树的删除操作可能会影响树的结构,因此需要对树进行平衡操作,以保证二叉搜索树的性质不被破坏。
二叉搜索树的删除时间复杂度为O(log n),其中n为二叉搜索树中节点的个数。
🍍二叉搜索树的查找、插入、删除实现
- 二叉搜索树节点的定义
template<class k>
class BStreeNode
{
public:BStreeNode(const k& key):_key(key), _left(nullptr), _right(nullptr){}k _key;BStreeNode* _left;BStreeNode* _right;
};
二叉搜索树节点的定义有以下成员:
-
key:表示节点的关键码,用于比较节点的大小关系,通常是一个模板类型,可以是整型、字符型、字符串、自定义类型等。
-
left:表示节点的左子节点,通常是一个指向BStreeNode类型的指针,如果节点没有左子节点,则该指针为空指针nullptr。
-
right:表示节点的右子节点,通常是一个指向BStreeNode类型的指针,如果节点没有右子节点,则该指针为空指针nullptr。
- 二叉搜索树的定义
template<class k>
class BStree
{typedef BStreeNode<k> Node;
public:Node* find(const k& key);bool insert(const k& key);bool erase(const k& key); void InOrder();
private:Node* _root = nullptr;void _InOrder(const Node* root);
};
二叉搜索树的定义包括以下成员:
-
Node:表示二叉树的节点,通常是一个模板类,包括节点的关键码、左子节点、右子节点等成员。
-
find():用于在二叉树中查找指定关键码的节点,如果找到,则返回该节点的指针;否则返回空指针nullptr。
-
insert():用于向二叉树中插入一个新节点,如果插入成功,则返回true;否则返回false。
-
erase():用于从二叉树中删除指定关键码的节点,如果删除成功,则返回true;否则返回false。
-
InOrder():用于对二叉树进行中序遍历,按照节点的关键码从小到大输出节点的值。
- 二叉搜索树查找实现
Node* find(const k& key){Node* cur = _root;while (cur){if (cur->_key < key) cur = cur->_right; else if (cur->_key > key)cur = cur->_left;elsereturn cur;}return nullptr;}
二叉搜索树的查找操作可以通过比较节点的键值来实现。从根节点开始,若当前节点的键值小于要查找的键值,则继续在右子树中查找;若当前节点的键值大于要查找的键值,则继续在左子树中查找;若当前节点的键值等于要查找的键值,则返回当前节点。
上述代码实现了二叉搜索树的查找操作。从根节点开始,通过循环遍历整棵树,比较节点的键值,根据大小关系移动到左子树或右子树中,直到找到要查找的节点或遍历到叶子节点为止。如果找到了要查找的节点,则返回该节点指针;否则返回空指针。
- 二叉搜索树插入实现
bool insert(const k& key){//空树if (_root == nullptr){Node* newnode = new Node(key);_root = newnode;return true;}//不为空Node* cur = _root;Node* parent = nullptr;while (cur){parent = cur;if (cur->_key < key)cur = cur->_right;else if (cur->_key > key)cur = cur->_left;elsereturn false;}Node* newnode = new Node(key);parent->_key > key ? parent->_left = newnode : parent->_right = newnode;return true;}
二叉搜索树的插入操作可以通过比较节点的键值来实现。从根节点开始,若要插入的键值小于当前节点的键值,则继续在左子树中插入;若要插入的键值大于当前节点的键值,则继续在右子树中插入;若要插入的键值等于当前节点的键值,则返回插入失败。
上述代码实现了二叉搜索树的插入操作。首先判断树是否为空,如果为空,则直接将新节点作为根节点;否则,从根节点开始循环遍历整棵树,比较节点的键值,根据大小关系移动到左子树或右子树中,直到找到合适的插入位置或遍历到叶子节点为止。如果找到了合适的插入位置,则创建新节点并插入到该位置;否则返回插入失败。
- 二叉搜索树删除的实现
bool erase(const k& key){//查找该节点及其父亲节点Node* cur = _root;Node* parent = nullptr;while (cur){if (cur->_key < key){parent = cur;cur = cur->_right;}else if (cur->_key > key){parent = cur;cur = cur->_left;} elsebreak;}if (cur == nullptr)return false;//为叶子节点else if (cur->_left == nullptr && cur->_right == nullptr)delete cur;//只有一个孩子else if ((cur->_left == nullptr && cur->_right) || (cur->_left && cur->_right == nullptr)){if (parent->_left == cur){cur->_left == nullptr ? parent->_left = cur->_right : parent->_left = cur->_left;}else{cur->_left == nullptr ? parent->_right = cur->_right : parent->_right = cur->_left;}delete cur;}//有两个孩子else if (cur->_left && cur->_right){Node* del = cur->_right;//找右子树最小节点while (del->_left){del = del->_left;}//赋值cur->_key = del->_key;//待删除节点的右指向最小节点右cur->_right = del->_right;//删除最小节点delete del;}return true;}
二叉搜索树的删除操作比较复杂,需要考虑删除节点的情况分为三种:
-
待删除节点为叶子节点:直接删除该节点即可。
-
待删除节点只有一个孩子:将该节点的孩子节点接到该节点的父节点上,然后删除该节点。
-
待删除节点有两个孩子:找到该节点的右子树中的最小节点,将其键值赋值给待删除节点,然后删除最小节点。
上述代码实现了二叉搜索树的删除操作。首先从根节点开始循环遍历整棵树,查找待删除节点及其父节点。如果没有找到待删除节点,则返回删除失败;否则根据待删除节点的情况进行不同的操作。如果待删除节点为叶子节点,则直接删除该节点;如果待删除节点只有一个孩子,则将孩子节点接到父节点上,然后删除该节点;如果待删除节点有两个孩子,则找到右子树中的最小节点,将其键值赋值给待删除节点,然后删除最小节点。最后返回删除成功。
- 二叉搜索树中序遍历实现
void _InOrder(const Node* root){if (root == nullptr)return;_InOrder(root->_left);cout << root->_key << ' ';_InOrder(root->_right);}
二叉搜索树的中序遍历是指按照节点键值的大小关系,先遍历左子树,再遍历根节点,最后遍历右子树。因为二叉搜索树的中序遍历结果是一个有序序列,因此可以使用中序遍历来实现对二叉搜索树的排序操作。
上述代码实现了二叉搜索树的中序遍历操作。首先判断当前节点是否为空,如果为空则返回;否则按照左子树、根节点、右子树的顺序递归遍历整棵树,并输出节点的键值。
🍋二叉搜索树的应用
-
K模型:K模型是指只有key作为关键码,结构中只需要存储Key即可,关键码即为需要搜索的值。例如,可以以词库中所有单词集合中的每个单词作为key,构建一棵二叉搜索树,在二叉搜索树中检索该单词是否存在,存在则拼写正确,不存在则拼写错误。
-
KV模型:KV模型是指每一个关键码key都有与之对应的值Value,即<Key, Value>的键值对。该种方式在现实生活中非常常见,例如英汉词典就是英文与中文的对应关系,通过英文可以快速找到与其对应的中文,英文单词与其对应的中文<word, chinese>就构成一种键值对;再比如统计单词次数,统计成功后,给定单词就可以快速找到其出现的次数,单词与其出现次数就是<word, count>就构成一种键值对。二叉搜索树可以用来实现KV模型,以key作为二叉搜索树的节点,value作为节点的值,通过比较key的大小关系来实现快速查找、插入和删除节点的操作。
将上述二叉搜索树修改为KV模型:
- 二叉树节点定义示例代码
template<class K, class V>
class BStreeNode
{
public:BStreeNode(const K& key, const V& value):_key(key), _value(value), _left(nullptr), _right(nullptr){}K _key;V _value;BStreeNode* _left;BStreeNode* _right;
};
- 中序输出代码:
void _InOrder(const Node* root){if (root == nullptr)return;_InOrder(root->_left);cout << root->_key << ":" << root->_value << endl;_InOrder(root->_right);}
- 测试代码:
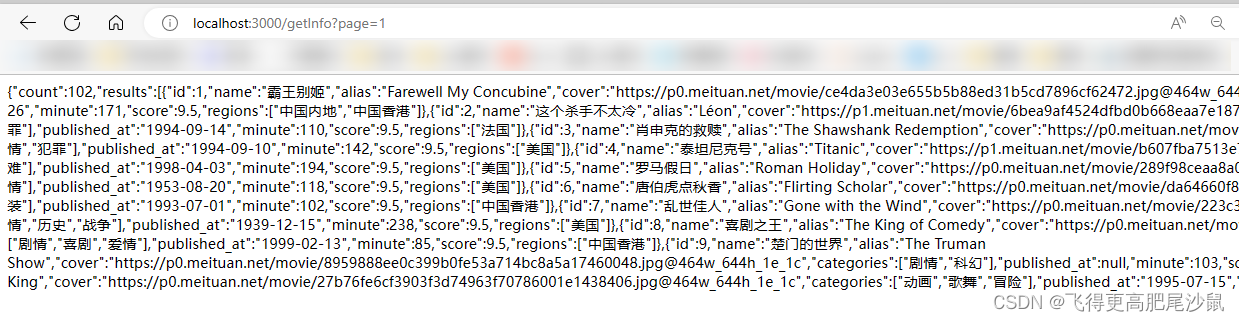
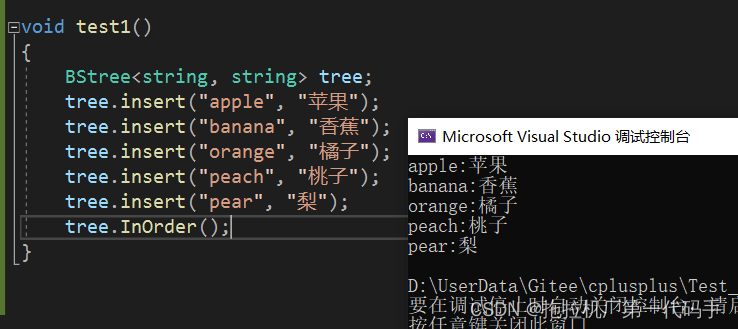
void test1()
{BStree<string, string> tree;tree.insert("apple", "苹果");tree.insert("banana", "香蕉");tree.insert("orange", "橘子");tree.insert("peach", "桃子");tree.insert("pear", "梨");tree.InOrder();
}
运行结果:
🥭二叉搜索树的性能分析
插入和删除操作都需要先进行查找操作,因此二叉搜索树的查找效率代表了二叉搜索树各个操作的性能。对于有n个节点的二叉搜索树,如果每个元素查找的概率相等,那么二叉搜索树的平均查找长度是节点在二叉搜索树的深度的函数,即节点越深,则比较次数越多。
需要注意的是,对于同一个关键码集合,如果各关键码插入的次序不同,可能会得到不同结构的二叉搜索树。因为二叉搜索树的结构取决于插入顺序,如果插入的顺序不同,可能会导致树的结构不同,进而影响树的查找效率。因此,在实际应用中,需要根据实际情况选择合适的插入顺序,以获得更好的性能。
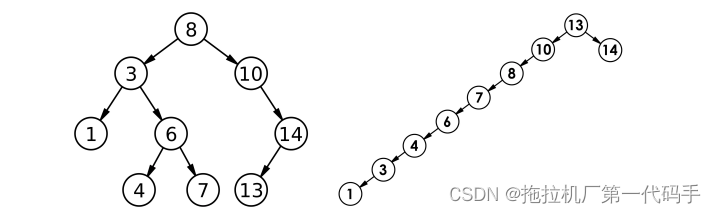
最优情况下,二叉搜索树的高度为 log2N,每一次查找可以将搜索范围缩小一半,因此平均比较次数为 log2N。
最差情况下,二叉搜索树的高度为 (N-1),每一次查找只能将搜索范围缩小一层,因此平均比较次数为 (1+2+…+N)/N = (N+1)/2,约等于 N/2。这种情况发生在插入的数据是有序的时候,导致二叉搜索树退化为链表。此时可以使用平衡二叉树来解决这个问题。
🍓总结
二叉搜索树是一种非常常见的数据结构,它是一棵二叉树,其中每个节点都包含一个键值,且左子树的所有节点的键值小于当前节点的键值,右子树的所有节点的键值大于当前节点的键值。这种特定的结构使得二叉搜索树能够快速地进行查找、插入、删除等操作。
在实际应用中,二叉搜索树被广泛使用,如在数据库索引、编译器符号表、路由表等领域。对于一个包含n个节点的二叉搜索树,其查找、插入、删除的时间复杂度均为O(logn),这使得它在处理大数据量时具有很高的效率。
但是,二叉搜索树也存在一些问题。当数据集合中的元素是随机分布的时,二叉搜索树的性能是非常好的。但是,当数据集合中的元素是有序的时,二叉搜索树的性能会退化为O(n),这就是所谓的“不平衡问题”。为了解决这个问题,我们可以使用平衡二叉树、红黑树等数据结构来优化二叉搜索树。
此外,二叉搜索树在插入重复元素时也存在问题。如果我们简单地将重复元素插入到二叉搜索树中,那么查找和删除操作就会变得非常麻烦。为了解决这个问题,我们可以使用多重集合、哈希表等数据结构来处理重复元素。
总之,二叉搜索树是一种非常重要的数据结构,它能够快速地进行查找、插入、删除等操作,但是在实际应用中需要注意避免和解决一些问题,如不平衡问题、重复元素问题等。
文章总结不易,如果觉得有所帮助的话就👍,文中所有代码均放在gitee上,关注博主,持续更新中…