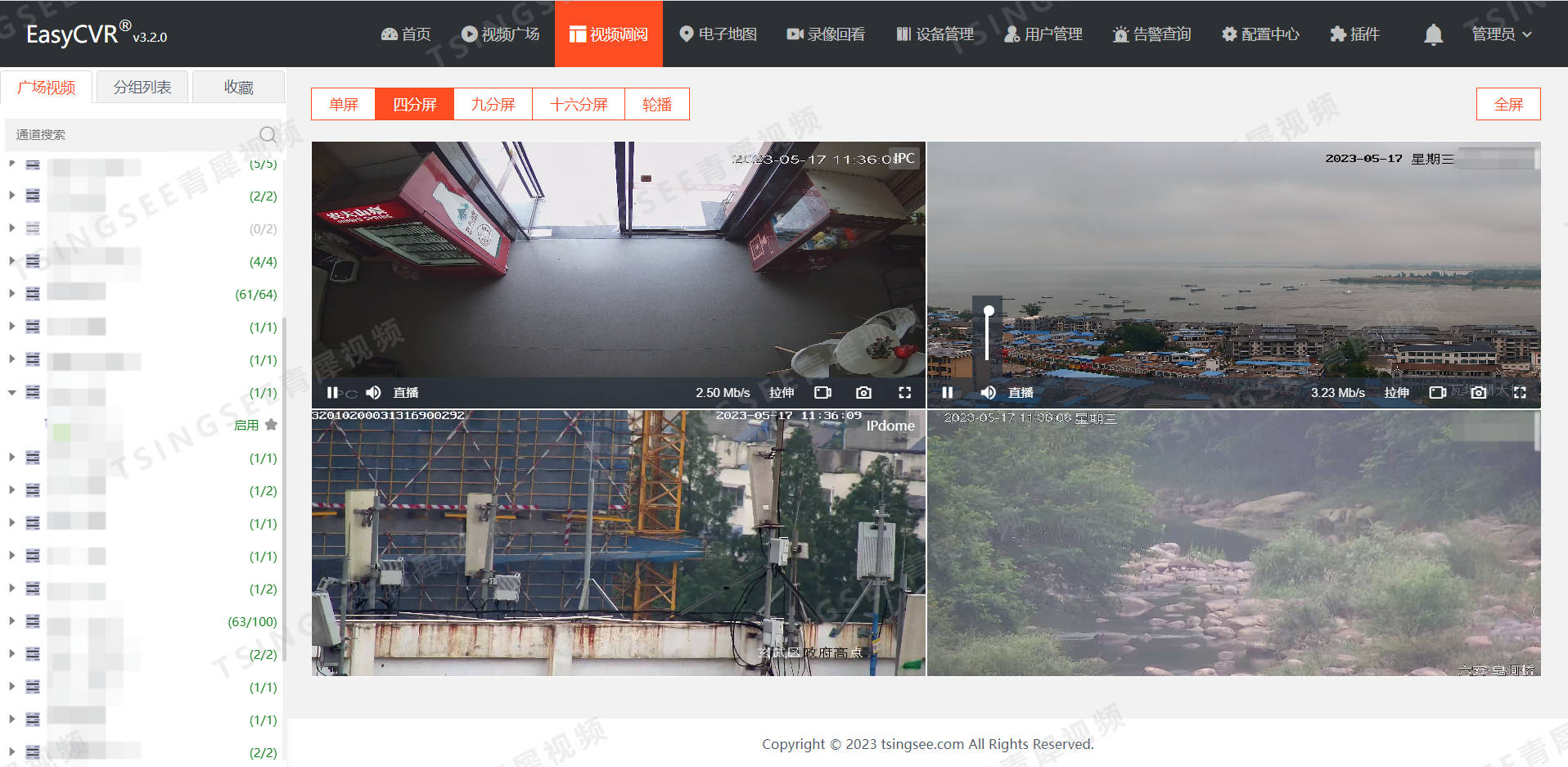
题目链接:https://www.acwing.com/problem/content/1312/

首先不考虑三点共线的情况一共有 种,现在来计算三点共线的情况
1.三点在一条直线上
2.三点在一条竖线上
3.三点在一条斜线上,正反斜线对称,仅需考虑一边的情况

如果边上两点A,B确定那么有多少种共线情况呢,如图所示一共gcd(a,b)-1种情况。
然后对于每组a,b一共有(n-a-1)*(m-b-1)种位置,枚举a,b即可
Code
#include <cstring>
#include <iostream>
#include <algorithm>using namespace std;typedef long long LL;int gcd(int a, int b)
{return b ? gcd(b, a % b) : a;
}LL C(int n)
{return (LL)n * (n - 1) * (n - 2) / 6;
}int main()
{int n, m;cin >> n >> m;n ++, m ++ ;LL res = C(n * m) - (LL)n * C(m) - (LL)m * C(n);for (int i = 1; i <= n; i ++ )for (int j = 1; j <= m; j ++ )res -= 2ll * (gcd(i, j) - 1) * (n - i) * (m - j);cout << res << endl;return 0;
}计算网格内所有三点共线线段的数量