常见的排序算法

常见的七大排序算法：

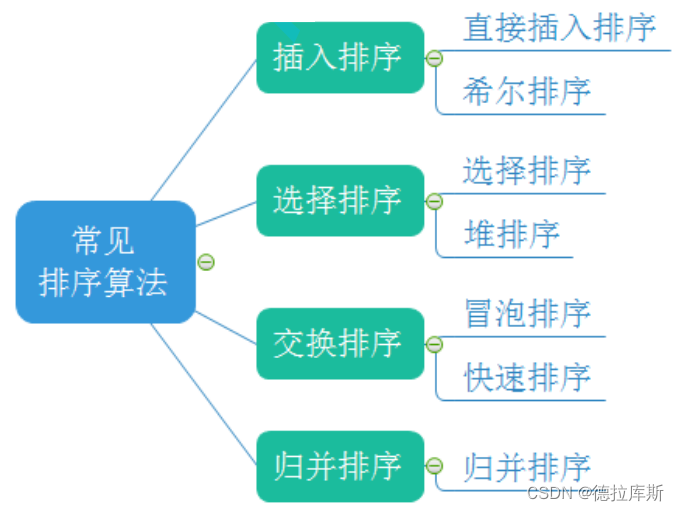
插入排序之直接插入排序

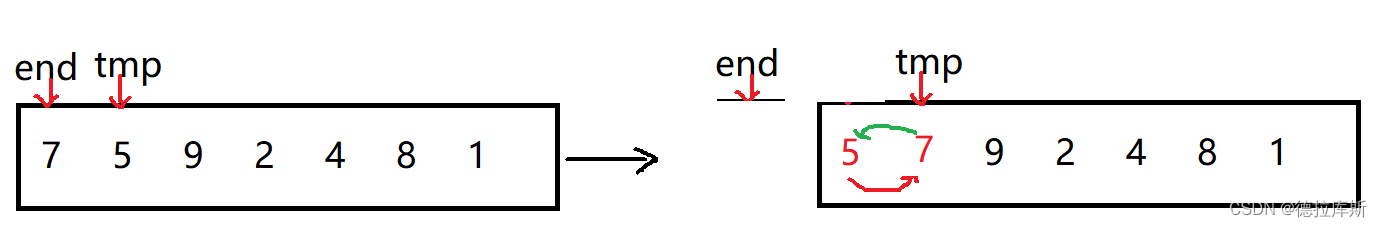
void InsertOrder(vector<int>& v)
{for (int i = 0; i < v.size() - 1; ++i){//起始end为0int end = i ;//比较的值是下标为end的下一个int tmp = v[end + 1];while (end >= 0){//如果end对应的值比tmp大，说明需要进行插入排序if (v[end] > tmp){v[end + 1] = v[end];//插入完成后end要向前走end--;}//如果end对应的值比tmp小，说明不需要进行插入，跳出当前while循环，end向后走即可elsebreak;}//一趟完成后，要将tmp赋给end的下一个位置v[end + 1] = tmp;}
}

时间复杂度

最好的情况是O(n)，数组为升序
最坏的情况是O(n2)，数组为降序

特性总结

1. 元素集合越接近有序，直接插入排序算法的时间效率越高
2. 时间复杂度：O(N^2)
3. 空间复杂度：O(1)，它是一种稳定的排序算法
4. 稳定性：稳定

插入排序之希尔排序

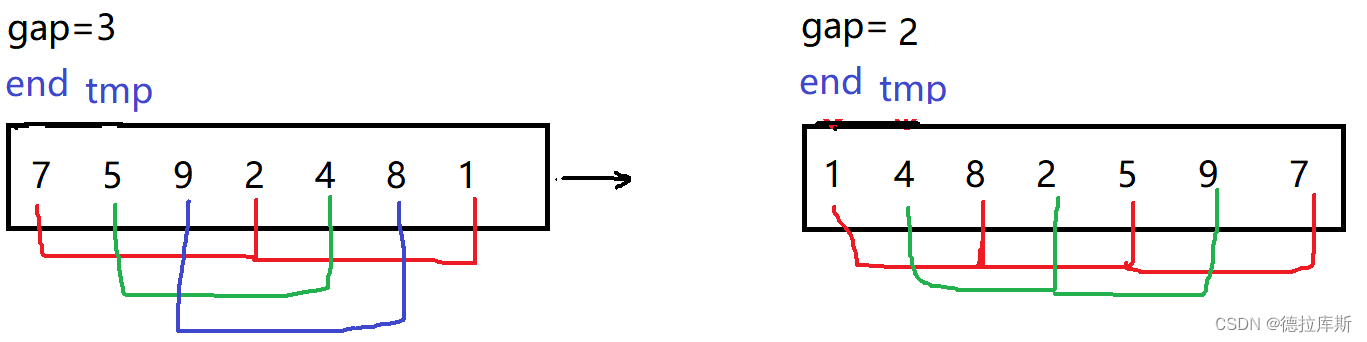
针对直接插入排序中，当数组属于降序时，时间复杂度太高，设计了希尔排序
设计思路是：当数组降序时，使用分组，可以减小排序次数，逐渐减小分组间隙，当排序次数较多时，数组本身已经快要接近有序了，以此来解决数据降序时排序复杂度高的问题。
因此希尔排序是对直接插入排序的优化

void ShellSort(vector<int>& v)
{int gap = v.size();while (gap > 1){gap = gap / 3 + 1;for (int i = 0; i < v.size() - gap; ++i){int end = i ;int tmp = v[end + gap];while (end >= 0){if (v[end] > tmp){v[end + gap] = v[end];end -= gap;}elsebreak;}v[end + gap] = tmp;}}
}

时间复杂度

O(n1.25)

选择排序之直接选择排序

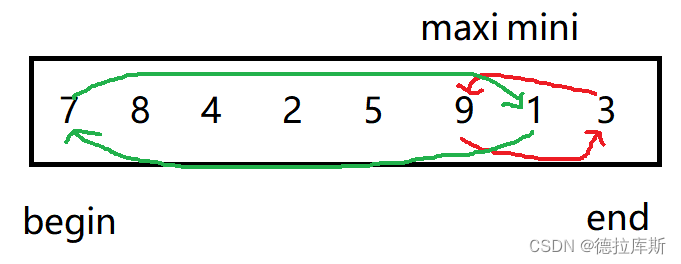
设计思路是：
1.从前往后遍历整个数组，拿到当前数组最大和最小值
2.将最小值和第一个元素交换，最大值和最后一个元素交换
3.缩小数组的范围，继续上述的操作
4.直到新数组范围内只有一个元素为止

void swap(int* a, int* b)
{int tmp = *a;*a = *b;*b = tmp;
}
void SelectSort(vector<int>& v)
{int begin = 0;int end = v.size() - 1;while (begin < end){int mini = begin;int maxi = begin;for (int i = begin; i <= end; ++i){if (v[mini] > v[i])mini = i;if (v[maxi] < v[i])maxi = i;}if (maxi == begin)maxi = mini;swap(&v[mini], &v[begin]);swap(&v[maxi], &v[end]);begin++;end--;}
}

特性总结

1. 直接选择排序思考非常好理解，但是效率不是很好。实际中很少使用
2. 时间复杂度：O(N^2)
3. 空间复杂度：O(1)
4. 稳定性：不稳定

选择排序之堆排序

思路：通过使用大堆或者小堆的思路，将数组进行排序
1.排升序建大堆，排降序建小堆
2.升序为例，先建一个大堆（双亲节点都大于左右孩子，根节点的值最大）
3.将数组最后一个位置的值和第一个位置的值交换
4.堆中除了最后一个节点，其余的节点进行调整，调整为新的大堆，将新的大堆的根节点值和倒数第二个节点的值交换
5.以此类推，直到当前新堆的范围为1停止
6.堆排序完成

void adjustDown(int* a, int n, int parent) {int child = parent * 2 + 1;while (child < n){if (child+1 < n && a[child] < a[child + 1]) {child++;}if (a[child] > a[parent]) {Swap(&a[child], &a[parent]);parent = child;child = parent * 2 + 1;}else {break;}}
}
void HeapSort(int* a, int n) {//1、建堆//parent = (child-1)/2for (int i = (n-1-1)/2; i >= 0; i--){adjustDown(a, n, i);}//2、堆排序int end = n - 1;while (end > 0){Swap(&a[0], &a[end]);end--;adjustDown(a, end, 0);}
}

时间复杂度

O(nlogn)

特性总结

1. 堆排序使用堆来选数，效率就高了很多。
2. 时间复杂度：O(N*logN)
3. 空间复杂度：O(1)
4. 稳定性：不稳定

交换排序之冒泡排序

思想：就是从前往后，依次判断当前位置的值和后一个位置的值关系，如果当前值大于后一个位置的值，就进行交换，这样将最大的值就放到的最后面，依次让数组的范围从后往前减小，循环遍历数组，就可完成排序

void BobbleSort(int* v, int size)
{int exchage = 0;for (int i = 0; i < size ; ++i){for (int j = 0; j < size - i - 1; ++j){if (v[j] > v[j + 1]){swap(v[j], v[j + 1]);exchage = 1;}}if (exchage == 0)break;}
}

特性总结

1. 冒泡排序是一种非常容易理解的排序
2. 时间复杂度：O(N^2)
3. 空间复杂度：O(1)
4. 稳定性：稳定

交换排序之快速排序

hoare版本

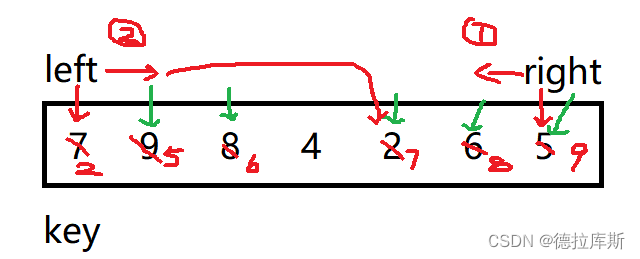
思想：将某个元素作为基准值，数组被该元素分为两个子数组，左子数组中的值均小于基准值，右子数组中的值均大于基准值，左右子数组重复上述过程，最终实现排序

做法：
1.先设置数组的第一个元素为基准值，设置第一个位置为左，最后一个位置为右
2.右先走，找比基准值小的，左后走，找比基准值大的
3.交换左右两个位置的值
4.右继续向左走，左继续向右走
以上的条件都是在左小于右的基础上进行的
5.如果相遇则将基准值和相遇值交换，函数返回相遇点

int _QuickSort(int* v, int left, int right)
{int k = left;while (left < right){//从右往左遍历，找比k小的数while (left < right && v[right] >= v[k]){right--;}//从左往右遍历，找比k大的数while (left < right && v[left] <= v[k]){left++;}//找到之后，进行交换swap(&v[left], &v[right]);}//如果相遇，将相遇点和数组左边的值交换swap(&v[left], &v[k]);return left;
}
void QuickSort(int* v, int left, int right)
{if (left >= right)return;int meet = _QuickSort(v, left, right);QuickSort(v, left, meet - 1);QuickSort(v, meet + 1, right);
}

挖坑法

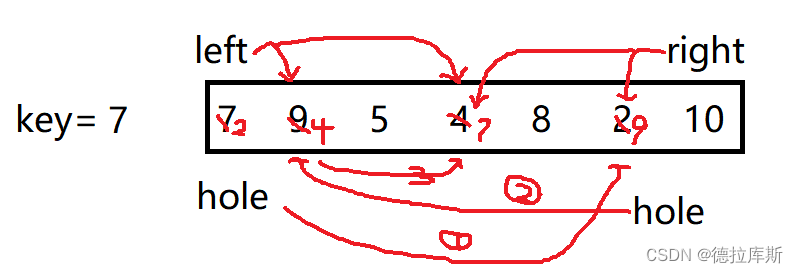
思路：
将某个元素作为基准值，数组被该元素分为两个子数组，左子数组中的值均小于基准值，右子数组中的值均大于基准值，左右子数组重复上述过程，最终实现排序
做法：
1.设置一个坑，hole为最左边的下标，一个key值
2.让右下标向左走，找比key对应值小的，让坑对应的值赋给右下标位置，并且让右下标表示为hole
3.让左下标向右走，找比key对应值大的，让坑对应的值赋给左下标位置，并且让左下标表示为hole
如果遇到左下标大于等于右下标的情况，则将key对应的值赋给相遇点
上述操作是在左小于右的范围下进行的
4.递归进行上述操作

int _QuickSort1(int* v, int left, int right)
{int hole = left;int key = v[left];while (left < right){while (left < right && v[right] >= key)right--;v[hole] = v[right];hole = right;while (left < right && v[left] <= key)left++;v[hole] = v[left];hole = left;}v[left] = key;return left;
}
void QuickSort1(int* v, int left, int right)
{if (left >= right)return;int meet = _QuickSort1(v, left, right);QuickSort1(v, left, meet - 1);QuickSort1(v, meet + 1, right);
}

双指针法

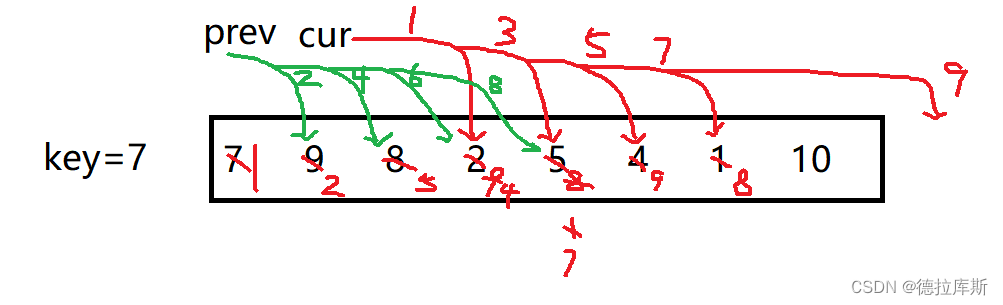
思想：和hoare版本和hole版本相似，都是将当前数组分为两个子数组，递归进行排序
做法：
1.设置key等于数组的左下标，left和right分别是数组的最左和最右，设置prev为左，prev的下一个为cur
2.先让cur向右走，找比key对应的值小的数
3.让prev++，交换prev和cur对应的两个数
4.继续上述操作
5.当cur超出right范围时，停止循环，让key和prev对应的值交换

int _QuickSort2(int* v, int left, int right)
{int prev = left;int cur = left + 1;int key = left;while (cur <= right){if (v[cur] < v[key]){prev++;swap(&v[prev], &v[cur]);}cur++;}swap(&v[key], &v[prev]);return prev;
}
void QuickSort(int* v, int left, int right)
{if (left >= right)return;int meet = _QuickSort2(v, left, right);QuickSort(v, left, meet - 1);QuickSort(v, meet + 1, right);
}

快速排序的优化1，增加三数取中

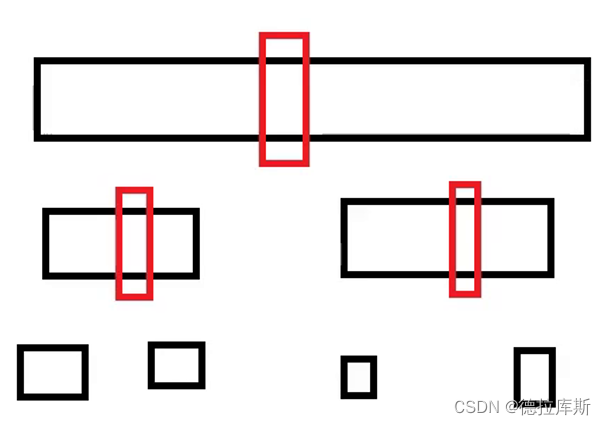
快速排序由于其思想是：根据基准值将数组划分为两个子区间，通过不断的划分子区间将其进行排序，但是当被排序数组是有序的，那么就会退化成下面图示的情况，导致复杂度为O(n2)。

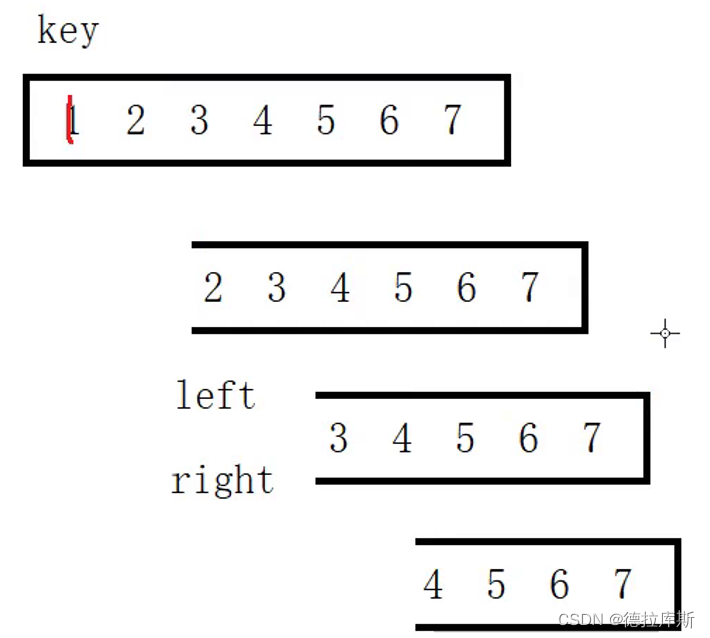
使用三数取中的方式，将数组可以平均二分，从而提高效率

//三数取中算法
int SelectMidIndex(int* v, int left, int right)
{int mid = left + (right - left) >> 1;if (v[left] > v[mid]){if (v[right] < v[mid])return mid;else if (v[right] > v[left])return left;else return right;}else //v[left] < v[mid]{if (v[right] > v[mid])return mid;else if (v[right] < v[left])return left;else return right;}
}
//hoare版本
int _QuickSort(int* v, int left, int right)
{int mid = SelectMid(v, left, right);swap(v[mid], v[left]);int k = left;while (left < right){//从右往左遍历，找比k小的数while (left < right && v[right] >= v[k]){right--;}//从左往右遍历，找比k大的数while (left < right && v[left] <= v[k]){left++;}//找到之后，进行交换swap(&v[left], &v[right]);}//如果相遇，将相遇点和数组左边的值交换swap(&v[left], &v[k]);return left;
}//hole版本
int _QuickSort1(int* v, int left, int right)
{int mid = SelectMid(v, left, right);swap(v[mid], v[left]);int hole = left;int key = v[left];while (left < right){while (left < right && v[right] >= key)right--;v[hole] = v[right];hole = right;while (left < right && v[left] <= key)left++;v[hole] = v[left];hole = left;}v[left] = key;return left;
}//双指针法
int _QuickSort2(int* v, int left, int right)
{int mid = SelectMidIndex(v, left, right);swap(&v[mid], &v[left]);int prev = left;int cur = left + 1;int key = left;while (cur <= right){if (v[cur] < v[key] && ++prev != cur)swap(&v[prev], &v[cur]);cur++;}swap(&v[key], &v[prev]);return prev;
}

快速排序的优化2，将递归算法改为非递归算法

我们可以将递归的快速排序算法改为非递归的方法，采用栈的数据结构作为辅助
思想：把之前递归版本的方法，通过循环放入栈来实现

做法：

1. 将当前数组的左右下标都放入栈中
2. 判断栈是否为为空，若不为空，则出栈，进行快速排序获取基准值的位置
3. 通过基准值将当前数组再次划分为左右两个子数组
4. 判断划分完之后的数组是否需要再次划分（判断条件是数组大小是否为1）

int _QuickSort1()
{//此处可以使用hoare，hole，双指针法
}
void QuickSort(int* v, int left, int right)
{stack<int> s;//先push右边界，再push左边界，这样后序取栈顶元素时的顺序就是左-->右s.push(right);s.push(left);while(!s.empty()){int begin = s.top();s.pop();int end = s.top();s.pop();//此时需要使用快速排序的函数，找中间值int meet = _QuickSort1(a, begin, end);//此时本质上是通过meet将数组分为了[begin,meet-1]和[meet+1,end]两部分，需要判断是否继续放入栈中if(meet-1 > begin){s.push(meet-1);s.push(begin);}if(end > meet + 1){s.push(end);s.push(meet+1);}}
}

快速排序的性能总结

1. 快速排序整体的综合性能和使用场景都是比较好的，所以才敢叫快速排序
2. 时间复杂度：O(N*logN)
3. 空间复杂度：O(logN)
4. 稳定性：不稳定

归并排序

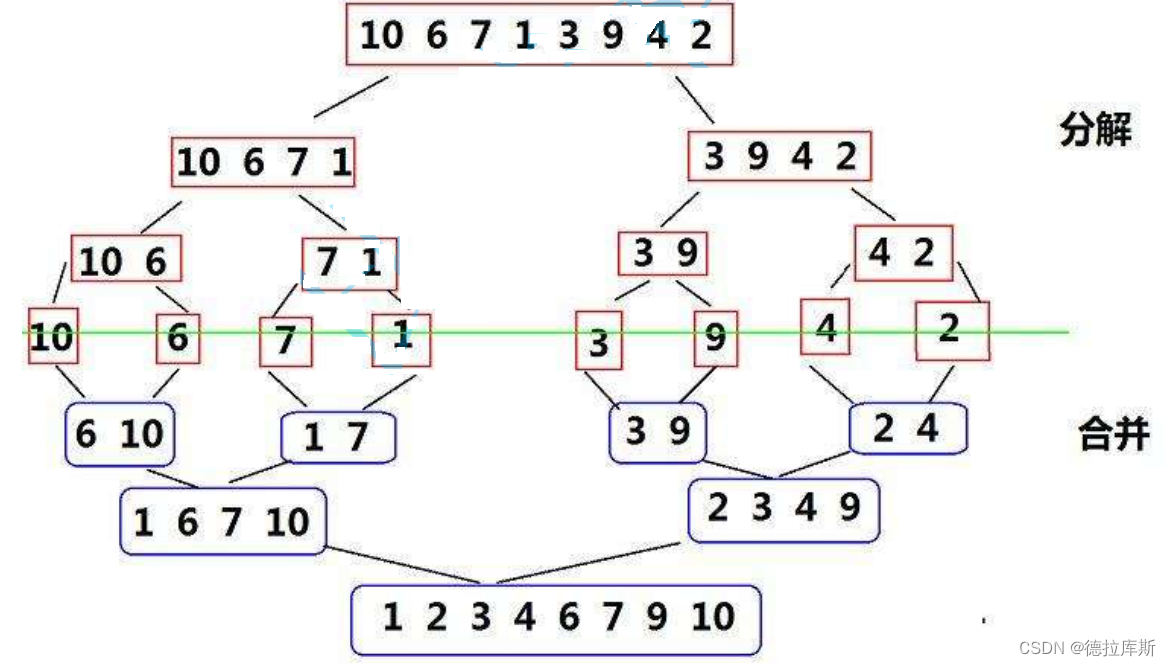
思路：采用分治法的思想，将已有的子序列合并，得到完全有序的序列，让每个子序列有序，再让两个有序列表合并为一个有序列表，称为二路归并
做法：

1. 将一个数组递归分解成左右大小皆为1的数组
2. 再对其进行排序（合并两个有序数组）
3. 将合并好的数组回写到原数组中

void _MargeSort(int* v, int left, int right, int* tmp)
{if (left >= right)return;int mid = left + (right - left)/2;_MargeSort(v, left, mid, tmp);_MargeSort(v, mid + 1, right, tmp);int begin1 = left;int end1 = mid;int begin2 = mid + 1;int end2 = right;int index = begin1;while (begin1 <= end1 && begin2 <= end2){if (v[begin1] < v[begin2])tmp[index++] = v[begin1++];else tmp[index++] = v[begin2++];}while(begin1 <= end1)tmp[index++] = v[begin1++];while (begin2 <= end2)tmp[index++] = v[begin2++];for (int i = left; i <= right; ++i)v[i] = tmp[i];
}
void MargeSort(int* v, int n)
{int left = 0;int right = n-1;int* tmp = (int*)malloc(n * sizeof(int*));_MargeSort(v, left, right, tmp);free(tmp);
}

归并排序特性总结

1. 归并的缺点在于需要O(N)的空间复杂度，归并排序的思考更多的是解决在磁盘中的外排序问题。
2. 时间复杂度：O(N*logN)
3. 空间复杂度：O(N)
4. 稳定性：稳定