前言:
图的基本概念:
若想简单绘制图可以利用此网站: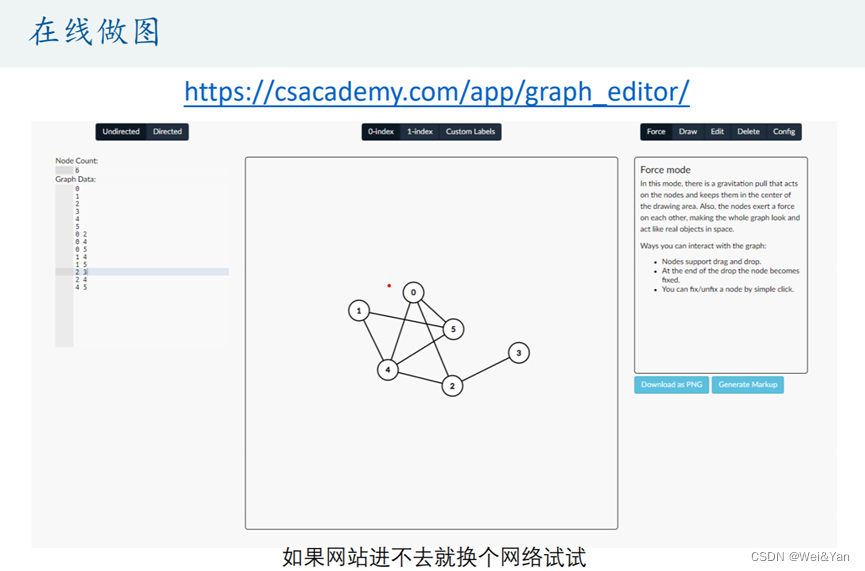
左上角Undirected/Directed是无向图/有向图
左边 0-index ,1-index为0下标,1下标。
Node Count为节点个数
Graph Data:最初尾节点的名称(一个数据)
相连两节点的名称与两节点连线的权重(三个数据)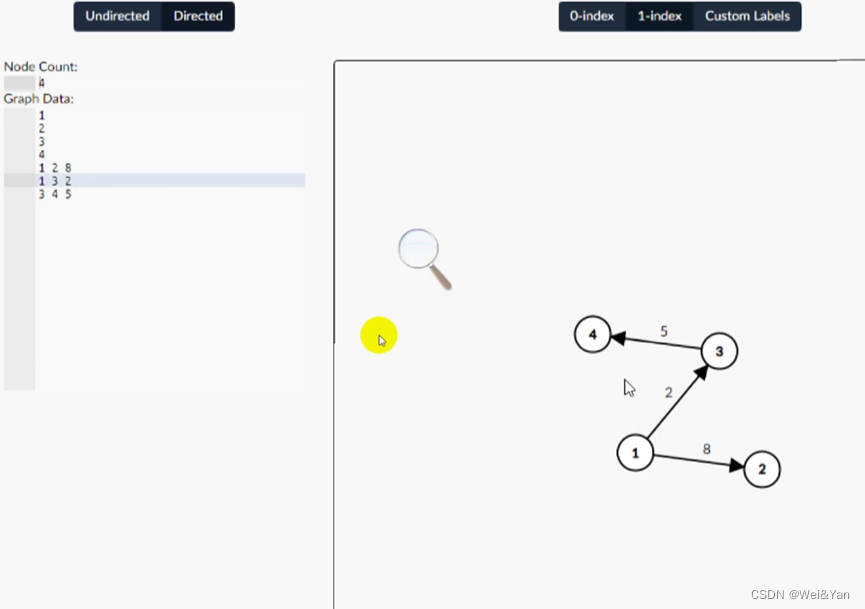
利用matlab制作 “图”:
Graph中的s,t指的图中顶点的名称,而且元素数量必须相同,s和t对应位置的数据会在构中相连。
注意事项:
- 在结点名称中若我们使用的是字符串,需要用大括号{},中间的字符名称需要用 ‘’引起。

2.若结点名为常数,这些结点必须都是从1开始的正整数。
Graph中的第三个元素为权重,权重对应的则是节点之间相连的线。
Matlab中的有向图:
函数为:digraph()
无向图的权重邻接矩阵: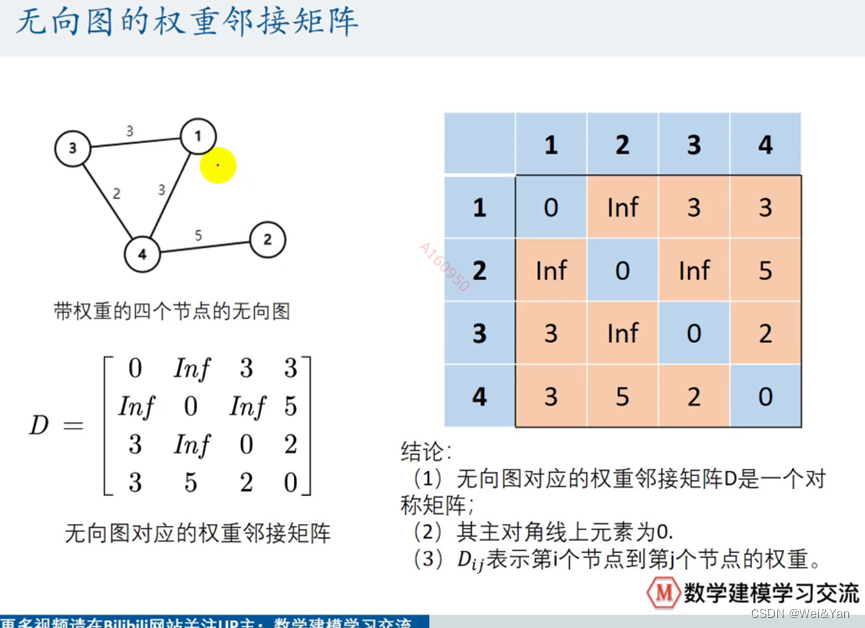
有向图的权重邻接矩阵:
求最小路径的算法:迪杰斯特拉算法:
博主之前在学习数据结构的时候创作过一篇关于迪杰斯特拉的文章:数据结构 -最短路径dijkstra(迪杰斯特拉)算法讲解及代码实现_地杰斯特拉_Wei&Yan的博客-CSDN博客可以参考里面的内容。
迪杰斯特拉的缺点:
如何修复该缺点:
什么是负权回路?
(注意无向图中的一条负权边也属于负权回路,如下图中结点3与结点2之间权重为-2的回路。)

在matlab中有计算最短路径的函数:
Shortserpath(图名称,起始节点,终点结点)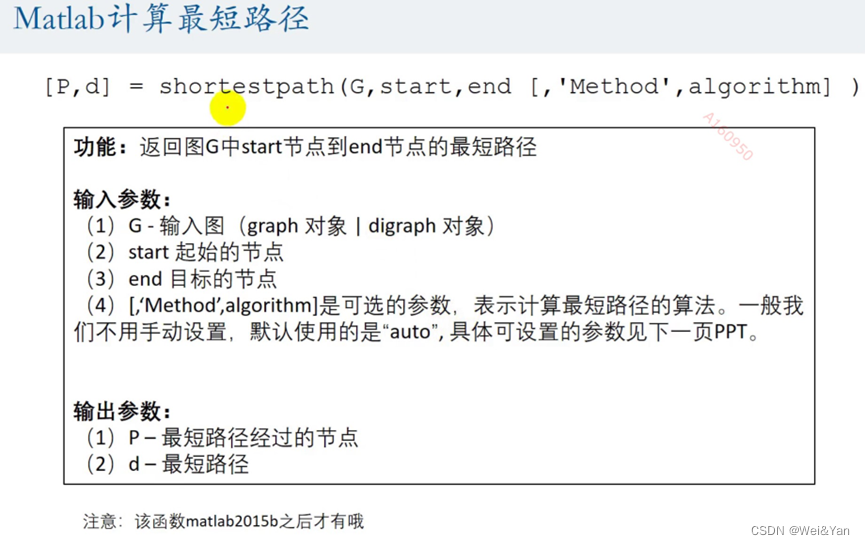
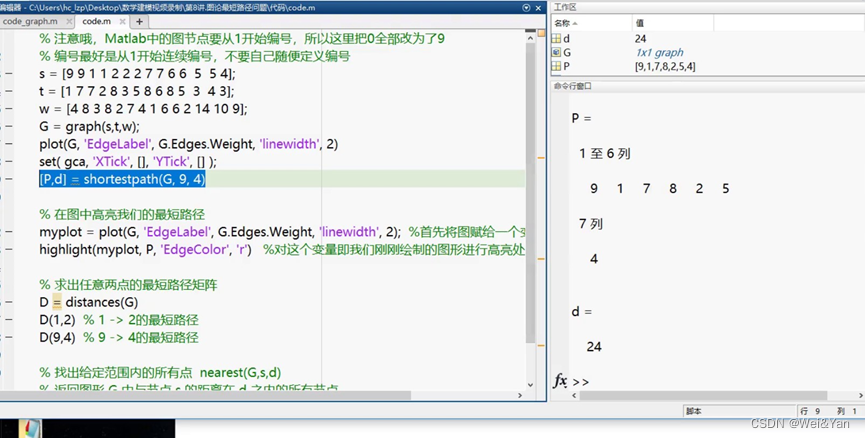
在图中高亮出图的最短路径
Highlight(plot的变量名,shortestpath中接受的P,‘EdgeColor’,‘颜色’)
返回任意两点的距离矩阵
找给定范围内所有的点: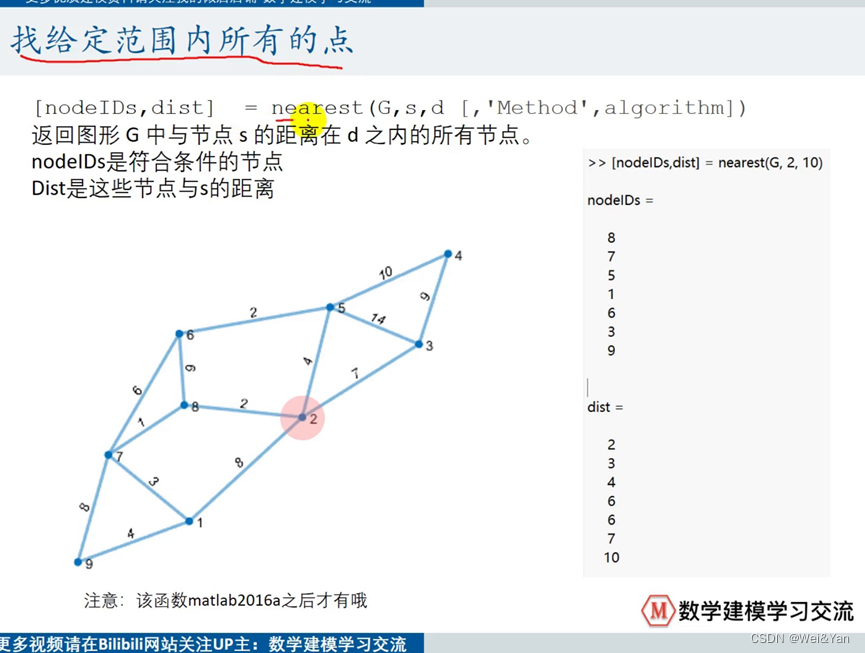
课后作业:
只需要找出最短路径和长度即可。(最好可以将最短路径) 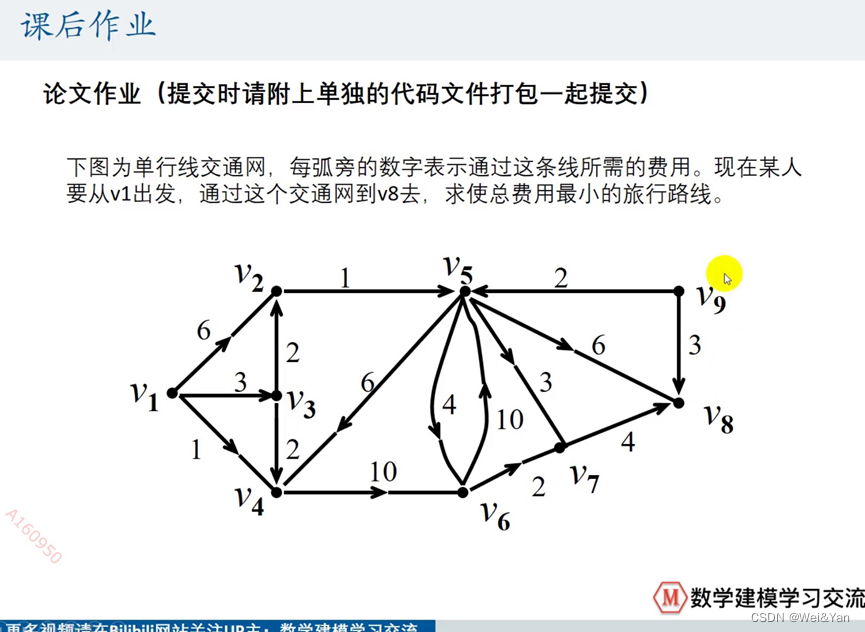
参考代码:
%创建图的顶点和边
s = {'v1','v1','v1','v2','v3','v3','v4','v5','v5','v5','v5','v6','v6','v7','v9','v9'};
t = {'v4','v2','v3','v5','v4','v2','v6','v4','v6','v7','v8','v5','v7','v8','v5','v8'};
w = [1,6,3,1,2,2,10,6,4,3,6,10,2,4,2,3];
G = digraph(s,t,w);
myplot = plot(G,'EdgeLabel',G.Edges.Weight,'LineWidth',2);%求出最短路径
[P,d] = shortestpath (G,'v1','v8')
highlight (myplot,P,'EdgeColor','red')博主曾经也写过一篇关于数据结构图的博客 :图的基本概念和术语_Wei&Yan的博客-CSDN博客