一、介绍
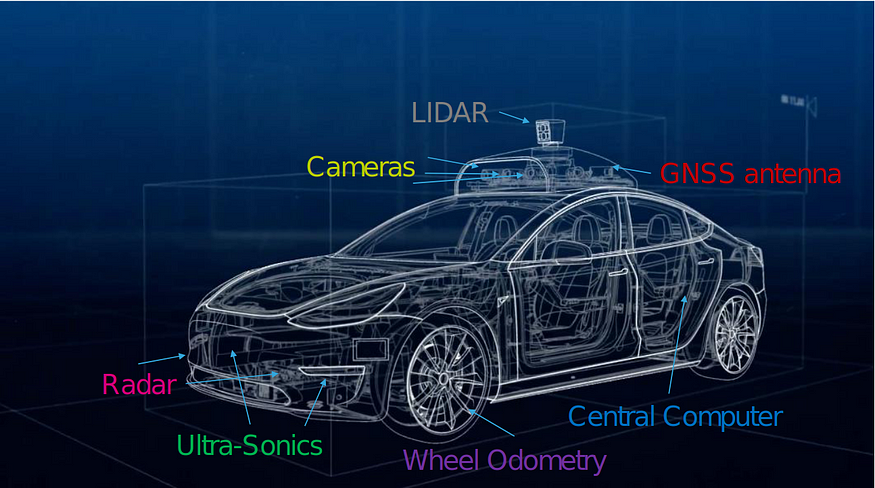
自动驾驶汽车配备了多个传感器,如摄像头、雷达、激光雷达等。如下图所示,所有传感器都有一些优点和缺点。但是,如果您融合不同传感器的输出,那么它们在任何天气条件下都不会失效。
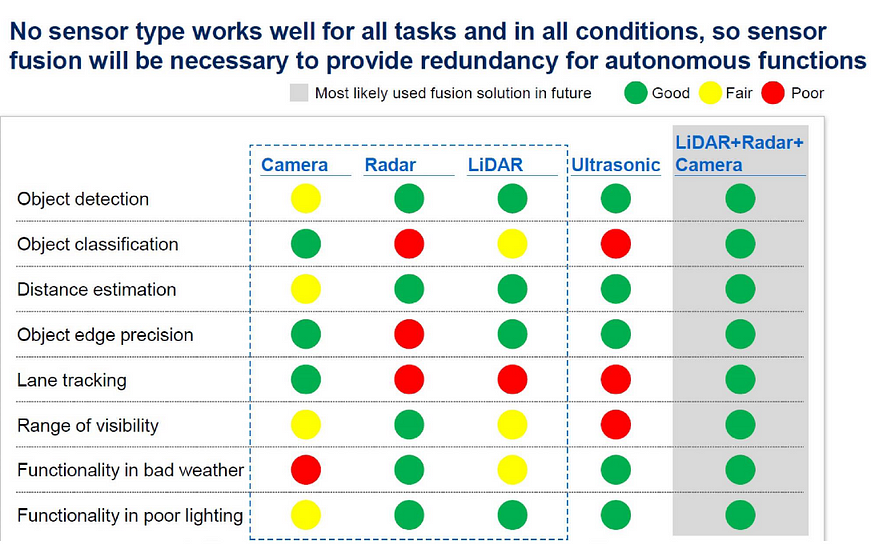
以下是有关它们在不同任务和天气条件下的表现的一些数据:
假设,我们要测量不同障碍物与给定汽车的距离(深度)。
- 可以使用具有立体声设置的摄像机测量距离。(请查看我的文章更多信息 https://medium.com/@satya15july_11937/depth-estimation-from-stereo-images-using-deep-learning-314952b8eaf9)
- 距离也可以使用激光雷达测量。
如图1所示,如果我们能够融合立体相机和激光雷达的输出,那么我们的系统可以在任何条件下可靠地预测距离/深度。假设这是我们的问题,我们希望融合两个传感器的输出并预测距离或深度。
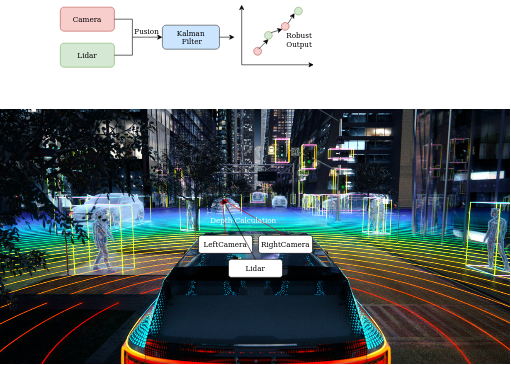
有很多方法可以融合不同传感器的输出,但在这里我们将讨论如何将它们与卡尔曼滤波器融合。
1.1 什么是卡尔曼滤波
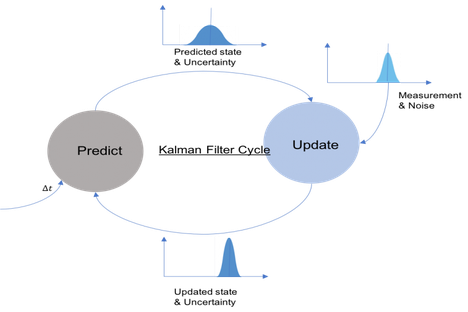
卡尔曼滤波器的基本思想是使用被测系统的模型,并在新的测量可用时更新模型。筛选器的工作原理是根据以前的状态估计值和系统模型对系统的当前状态进行预测,然后将此预测与新度量值相结合,以获得更新的状态估计值。
它基于贝叶斯定理,让我们简化卡尔曼滤波器:
- 你什么时候预测某种状态,这意味着你指的是概率分布。
- 概率分布具有均值和方差或协方差。
- 这是一个迭代过程,并尝试预测每一步的状态,并根据传感器的测量数据更新/纠正状态。
- 使用下面的公式,卡尔曼滤波器尝试预测和更新状态(X'/X)和不确定性(P'/P)。
1.2 卡尔曼滤波器的应用:
卡尔曼滤波器用于许多领域,例如
- 机器人/汽车的本地化,
- 跟踪对象(导弹、飞机、面部等)
- 融合来自多个传感器的数据。
- 经济学等
二、卡尔曼滤波器的类型
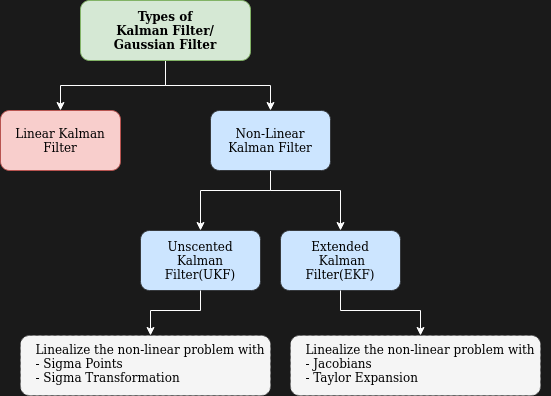
卡尔曼滤波器有以下类型:
- 线性卡尔曼滤波器
- 非线性卡尔曼滤波器。
- 无迹卡尔曼滤波器(UKF)- 扩展卡尔曼滤波器(EKF)
2.1 线性卡尔曼滤波器:
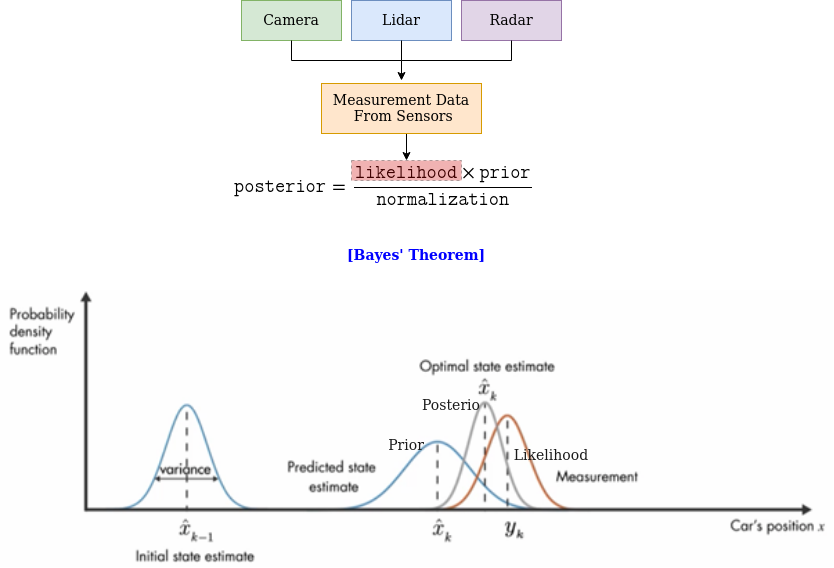
卡尔曼滤波预测不确定性(即方差),这就是为什么它用概率分布来表示,在这种情况下是高斯分布。
卡尔曼滤波器使用以下公式进行预测
后验 = 先前 * 测量/归一化器
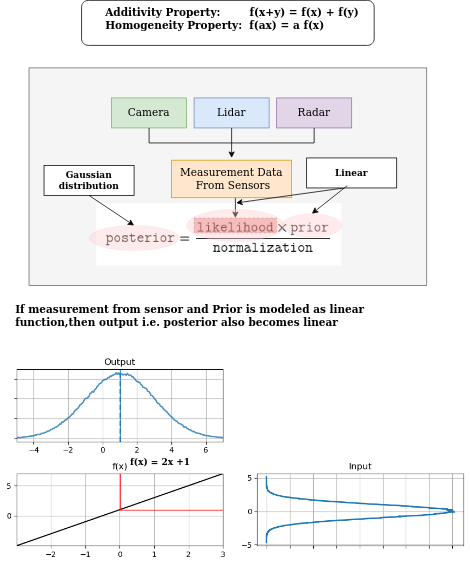
上述公式期望后验是高斯的,这只有在满足以下乘法和加法性质时才有可能。
- f(x+y) = f(x) + f(y)
- f(ax) = a f(x)
如果用于传感器的先验和测量的估计方法是线性的,则后验可以是高斯的。如果他们使用非线性方法,则不能使用线性卡尔曼滤波器。请检查下图。
2.2 非线性卡尔曼滤波器:
后验可以是非高斯的,如果在这种情况下使用的先验或似然(从传感器测量)方法 Non-Linear.In,则可以使用
- 无迹卡尔曼滤波(UKF)
- 利用西格玛点和变换方法对问题进行线性化处理 - 扩展卡尔曼滤波器(EKF)
- 使用雅可比和泰勒展开线性化问题。

以下是一些非线性示例:
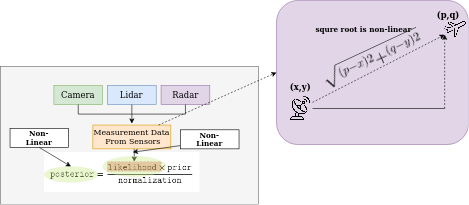
用于测量雷达和飞机之间倾斜距离的非线性方法
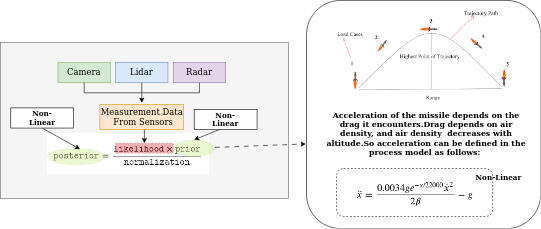
用于先验估计的非线性方法
线性卡尔曼滤波器是跳转到UKF和EKF之前的基础。在本文中,让我们重点介绍线性卡尔曼滤波器。
三、线性卡尔曼滤波器详情:
线性滤波器可以通过以下步骤进行设计:
- 设计状态变量和协方差。
- 设计过程模型。
- 设计控制模型/功能。
- 预测步骤(带先验)。
- 更新步骤(通过传感器测量)
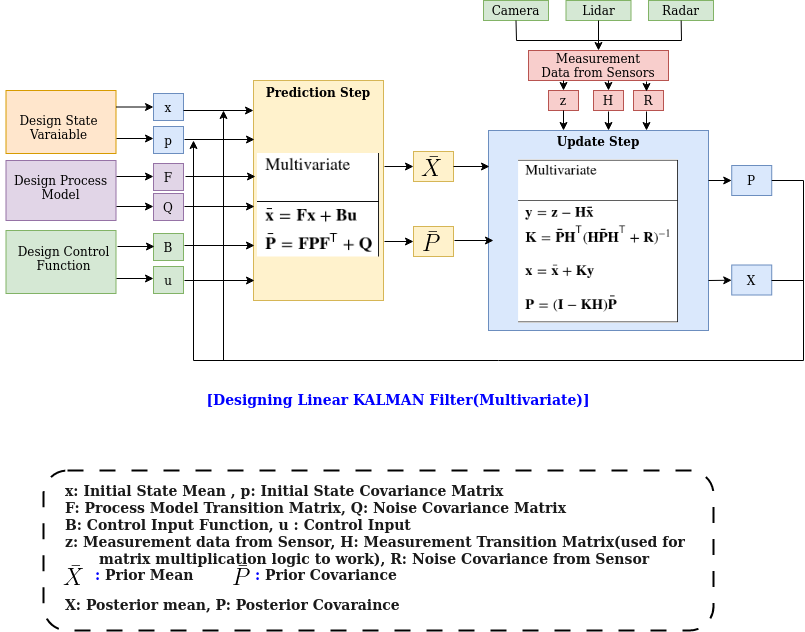
对于非线性滤波器,如无迹卡尔曼滤波器(UKF)和扩展卡尔曼滤波器(EKF),上述设计保持不变,但有一些例外,例如:
- UKF 使用西格玛点和无迹变换步骤,这是额外的。
- EKF 使用雅可比量对非线性问题进行线性化。
所以上图对于理解卡尔曼滤波非常重要,无论是线性的还是非线性的。
3.1. 设计状态变量和协方差:
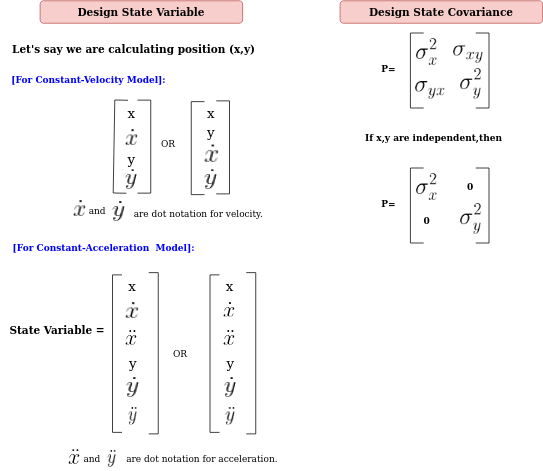
3.2. 设计过程模型:

3.3.设计控制功能:(B和你)
在卡尔曼滤波器中,控制函数用于将控制输入的影响合并到状态预测方程中。控制输入是用于影响系统演进的已知信号,可用于提高状态估计的准确性。
控制函数通常由矩阵 B 表示,该矩阵将控制输入映射到状态向量的变化,而您映射到控制输入
例如,机器人根据其当前位置与所需位置发送转向和速度信号。因此,在这种情况下,需要定义控制输入 U 和控制函数 B。如果没有关于输入控件的信息,则将 B 和 U 设置为 0。
控制功能在系统可能受到已知控制输入影响的情况下特别有用,例如在机器人或飞机控制中。通过将控制函数合并到状态预测方程中,卡尔曼滤波器可以利用控制输入的已知影响来提高状态估计的精度。
3.4. 预测步骤:
在卡尔曼滤波中,预测步骤是递归过程的第一步,它使用先前的状态估计及其协方差来预测当前状态估计及其协方差。预测步骤由两个子步骤组成:
- 状态预测(X')
- 协方差预测(P')
3.5 . 更新步骤:
在预测步骤之后,卡尔曼滤波器使用预测状态估计及其协方差来执行测量更新步骤,该步骤将新测量合并到状态估计中并更新其协方差和状态。
四、使用卡尔曼滤波器进行目标检测/对象跟踪
卡尔曼滤波器在许多计算机视觉应用中用于对象跟踪。我在驾驶员监控系统(DMS)中使用它,以提高低功耗设备上的FPS。
4.1 设计用于对象跟踪的卡尔曼滤波器:
对象检测(即ROI预测)是一个线性问题,让我们讨论如何实现它。
我已经分享了我的实现@https://github.com/satya15july/linear_kalman_filter。
4.2 Design 状态变量和协方差:
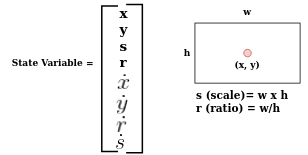
class KalmanTrack:def __init__(self, initial_state):self.kf = KalmanFilter(dim_x=8, dim_z=4)....self.kf.P[4:, 4:] *= 1000. # initial velocity error covarianceself.kf.P *= 10. # initial location error covariance self.kf.x[:4] = xxyy_to_xysr(initial_state) # initialize KalmanFilter state4.3 设计过程模型:
class KalmanTrack:def __init__(self, initial_state):....self.kf = KalmanFilter(dim_x=8, dim_z=4)# Transition matrixself.kf.F = np.array([[1, 0, 0, 0, 1, 0, 0, 0],[0, 1, 0, 0, 0, 1, 0, 0],[0, 0, 1, 0, 0, 0, 1, 0],[0, 0, 0, 1, 0, 0, 0, 1],[0, 0, 0, 0, 1, 0, 0, 0],[0, 0, 0, 0, 0, 1, 0, 0],[0, 0, 0, 0, 0, 0, 1, 0],[0, 0, 0, 0, 0, 0, 0, 1]])self.kf.Q[-1, -1] *= 0.01 # process noiseself.kf.Q[4:, 4:] *= 0.01 # process noise 4.4 .设计控制功能:
B 和 u 设置为 0,因为这在此给定方案中无效。
4. 预测步骤:
def predict(self):self.x = dot(self.F, self.x) # x = Fxself.P = dot(self.F, dot(self.P, self.F.T)) + self.Q # P = FPF' + Qself.x_prior = np.copy(self.x)self.P_prior = np.copy(self.P)5. 更新步骤:
def update(self, z):if self.debug_flag:print("KalmanFilter::update, z: {}".format(z))# y = z - Hx (Residual between measurement and prediction)y = z - np.dot(self.H, self.x)PHT = dot(self.P, self.H.T)# S = HPH' + R (Project system uncertainty into measurement space)S = dot(self.H, PHT) + self.R# K = PH'S^-1 (map system uncertainty into Kalman gain)K = dot(PHT, inv(S))# x = x + Ky (predict new x with residual scaled by the Kalman gain)self.x = self.x + dot(K, y)# P = (I-KH)PI_KH = self._I - dot(K, self.H)self.P = dot(I_KH, self.P)请检查我分享的完整代码@https://github.com/satya15july/linear_kalman_filter。
五、评估
在上面的视频中,您可以看到卡尔曼滤波器预测与对象检测器匹配。但在下面的视频中,卡尔曼滤波器预测最初与物体检测器不匹配,因为汽车的形状随帧到另一帧而变化。但是当形状停止波动时,预测会稳定下来。
预测的这种波动是否意味着我们不能使用卡尔曼滤波进行对象跟踪/目标检测?
让我们以驾驶员监控系统(DMS)中的人脸检测/跟踪用例为例,
- 通常,驾驶员专注于道路,不会经常移动。
- 因此,在这种情况下,我们可以在每个交替帧中使用卡尔曼滤波器进行人脸检测,并且我们可以使用一些智能,以便更多地将其用于人脸跟踪/人脸检测。
- 如果您可以做到这一点,那么您的驾驶员监控系统性能可以大大提高。不是吗?
这是统计数据(我从我的实现中收集的)
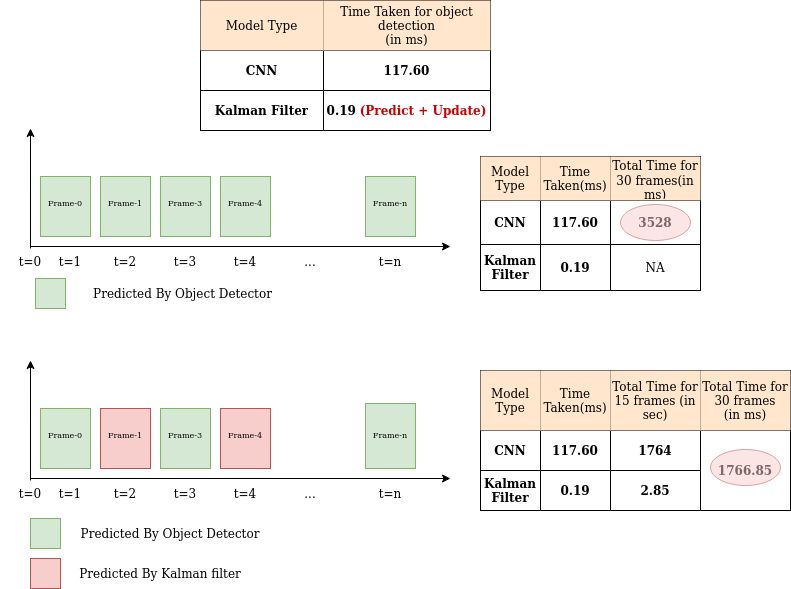
六、结论
我认为如果您仔细阅读本文,您可以了解如何使用卡尔曼滤波器融合不同的传感器。我将在下一篇文章中分享代码并解释。
在这里,我概述了什么是卡尔曼滤波器以及如何使用线性卡尔曼滤波器进行对象跟踪。但这个世界充满了非线性问题。机器人定位(SLAM)、跟踪飞机/导弹等问题是非线性问题,无法通过线性卡尔曼滤波解决。它可以使用 UKF 或 EKF 来解决。