💥💥💞💞欢迎来到本博客❤️❤️💥💥
🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。
⛳️座右铭:行百里者,半于九十。
📋📋📋本文目录如下:🎁🎁🎁
目录
💥1 概述
📚2 运行结果
🎉3 参考文献
🌈4 Matlab代码及数据
💥1 概述
基于UKF法和AUKF法的电力系统三相状态估计研究是一种利用无迹卡尔曼滤波(Unscented Kalman Filter, UKF)以及其改进算法(Augmented Unscented Kalman Filter, AUKF)来进行电力系统三相状态估计的研究方法。
在电力系统中,三相状态估计是指通过测量数据和系统模型来估计电力系统中三相电压和电流的实时状态。三相状态估计在电力系统的运行和控制中具有关键作用,能够提供对电力系统的潮流、功率、电压稳定性等信息的高精度估计。
UKF是一种无迹卡尔曼滤波算法,通过选取一组特定的采样点(无迹)来对高斯分布进行逼近。UKF对非线性系统具有较好的适应性和稳定性,可以应对电力系统中存在的非线性和复杂特性。
AUKF是对UKF的改进,通过引入额外的状态变量和噪声向量,使得状态估计过程更具鲁棒性。AUKF通常用于处理电力系统中的非线性模型和高维系统的状态估计问题。
基于UKF法和AUKF法的电力系统三相状态估计研究可以涉及以下内容:
1. 系统建模:建立电力系统的数学模型,包括节点和支路的等效电路模型,考虑电压相位差和幅值约束的关系等。
2. 观测模型:定义观测方程,将实时的测量数据与电力系统的状态变量联系起来。包括电压、电流以及其他传感器测量数据。
3. 无迹卡尔曼滤波:使用UKF或AUKF算法进行状态估计,根据测量数据和系统模型,通过递推的方式更新和估计电力系统的三相状态变量。
4. 非线性问题处理:考虑电力系统中的非线性和复杂特性,利用UKF和AUKF算法有效处理非线性观测方程和状态方程。
5. 算法优化:对滤波算法的参数进行优化调整,例如选择合适的采样点和权重,以提高估计准确性和收敛速度。
通过基于UKF法和AUKF法的研究,可以实现电力系统的三相状态估计,并提供准确的潮流、功率、电压稳定性等信息,支持电力系统的运行和控制。但需要注意的是,具体的研究需要结合实际电力系统的特点和要求来设计和优化算法。
📚2 运行结果

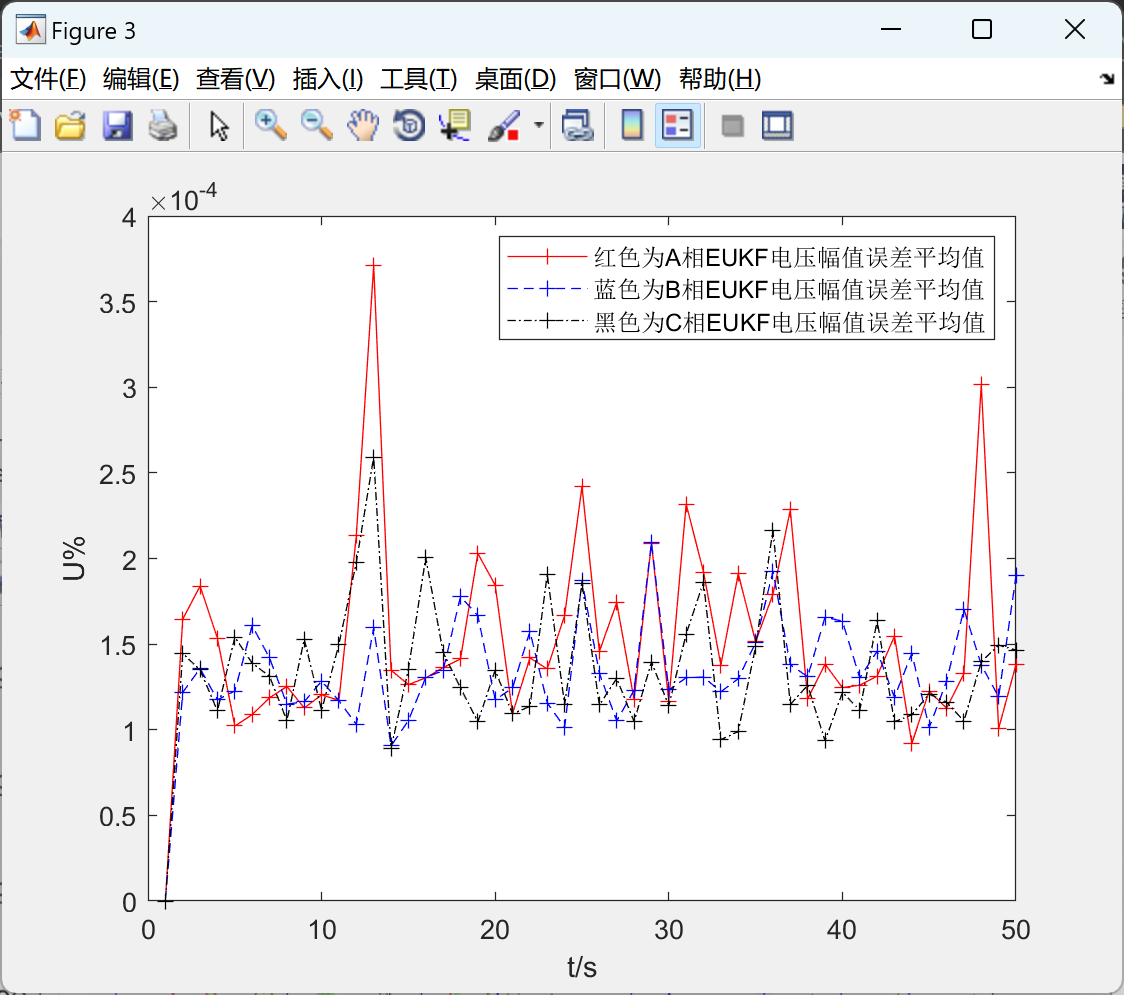
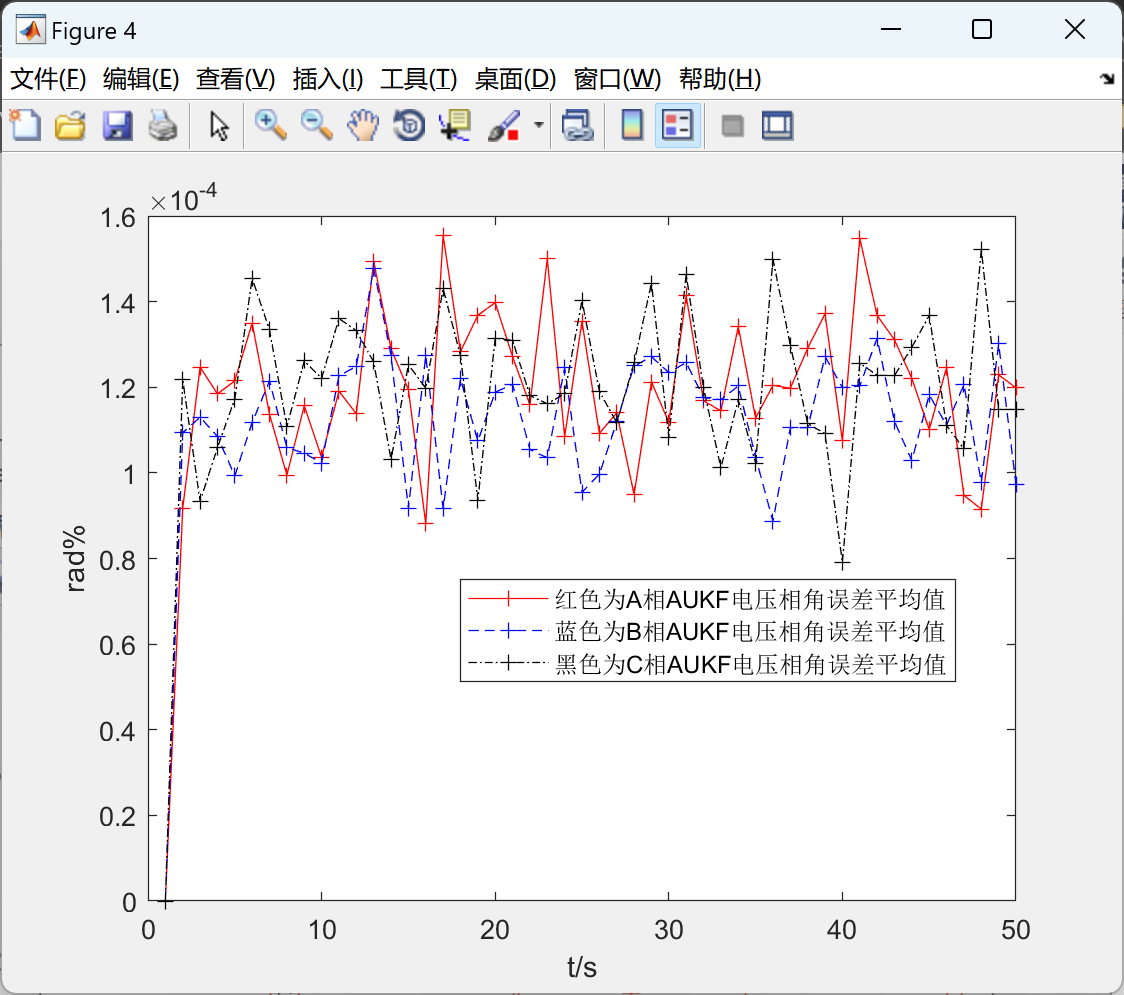
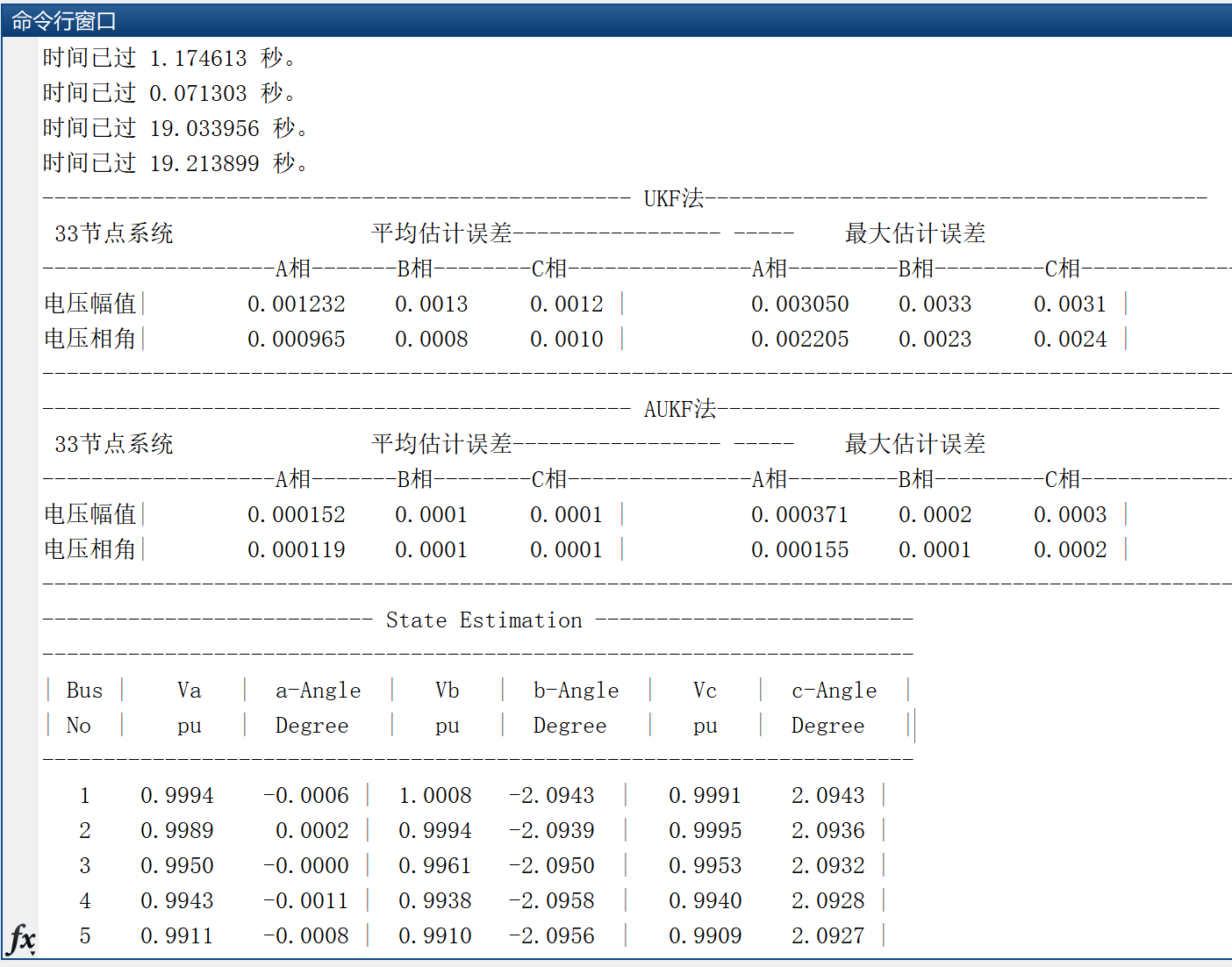
🎉3 参考文献
部分理论来源于网络,如有侵权请联系删除。
[1]卢云帆,邢丽坤,张梦龙等.基于UKF-AUKF锂电池在线参数辨识和SOC联合估计[J].电源技术,2022,46(10):1151-1155.
[2]王萍,弓清瑞,程泽等.基于AUKF的锂离子电池SOC估计方法[J].汽车工程,2022,44(07):1080-1087.DOI:10.19562/j.chinasae.qcgc.2022.07.014.