在本教程中,我们将学习如何训练PointNet进行分类。 我们将主要关注数据和训练过程; 展示如何从头开始编码 Point Net 的教程位于此处。 本教程的代码位于这个Github库中,我们将使用的笔记本位于这个Github库中。 一些代码的灵感来自于这个Github库。

推荐:用 NSDT设计器 快速搭建可编程3D场景。
1、获取数据
我们将使用只有 16 个类的较小版本的 shapenet 数据集。 如果你使用的是Colab,可以运行以下代码来获取数据。 警告,这将需要很长时间。
!wget -nv https://shapenet.cs.stanford.edu/ericyi/shapenetcore_partanno_segmentation_benchmark_v0.zip --no-check-certificate
!unzip shapenetcore_partanno_segmentation_benchmark_v0.zip
!rm shapenetcore_partanno_segmentation_benchmark_v0.zip
如果你想在本地运行,请访问上面第一行的链接,数据将自动下载为 zip 文件。
该数据集包含 16 个带有类标识符的文件夹(自述文件中称为“synsetoffset”)。 文件夹结构为:
synsetoffset|- points # 来自 ShapeNetCore 模型的均匀采样点|- point_labels # 每点分割标签|- seg_img #标签的可视化
train_test_split: #带有训练/验证/测试拆分的 JSON 文件
自定义 PyTorch 数据集位于此处,解释代码超出了本教程的范围。 需要了解的重要一点是,数据集可以获取 (point_cloud, class) 或 (point_cloud, seg_labels)。 在训练和验证期间,我们向点云添加高斯噪声,并围绕垂直轴(本例中为 y 轴)随机旋转它们。 我们还对点云进行最小-最大归一化,以便它们的范围为 0-1。 我们可以像这样创建 shapenet 数据集的实例:
from shapenet_dataset import ShapenetDataset# __getitem__ returns (point_cloud, class)
train_dataset = ShapenetDataset(ROOT, npoints=2500, split='train', classification=True)
2、探索数据
在开始任何训练之前,让我们先探讨一些训练数据。 为此,我们将使用 Open3d 版本 0.16.0(必须为 0.16.0 或更高版本)。
!pip install open3d==0.16.0
我们现在可以使用以下代码查看示例点云。 你应该注意到,每次运行代码时点云都会以不同的方向显示。
import open3d as o3
from shapenet_dataset import ShapenetDatasetsample_dataset = train_dataset = ShapenetDataset(ROOT, npoints=20000, split='train', classification=False, normalize=False)points, seg = sample_dataset[4000]pcd = o3.geometry.PointCloud()
pcd.points = o3.utility.Vector3dVector(points)
pcd.colors = o3.utility.Vector3dVector(read_pointnet_colors(seg.numpy()))o3.visualization.draw_plotly([pcd])
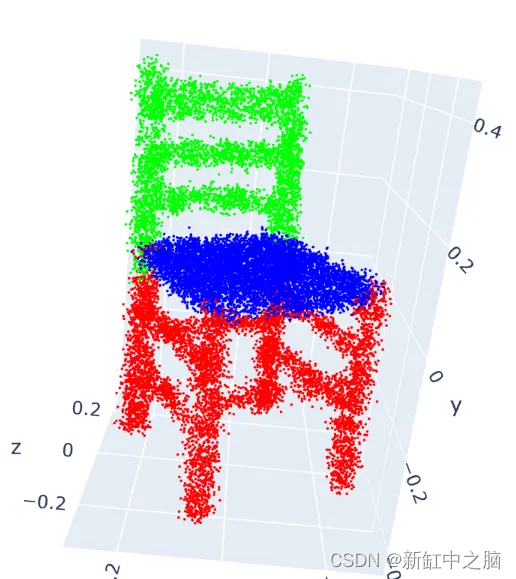
图 1.随机旋转的噪声点云。 Y 轴是纵轴
你可能不会注意到噪音有太大差异,因为我们添加的量很小; 我们添加了少量,因为不想极大地破坏结构,但这一小量足以对模型产生影响。 现在我们就来看看训练分类的数据频率。
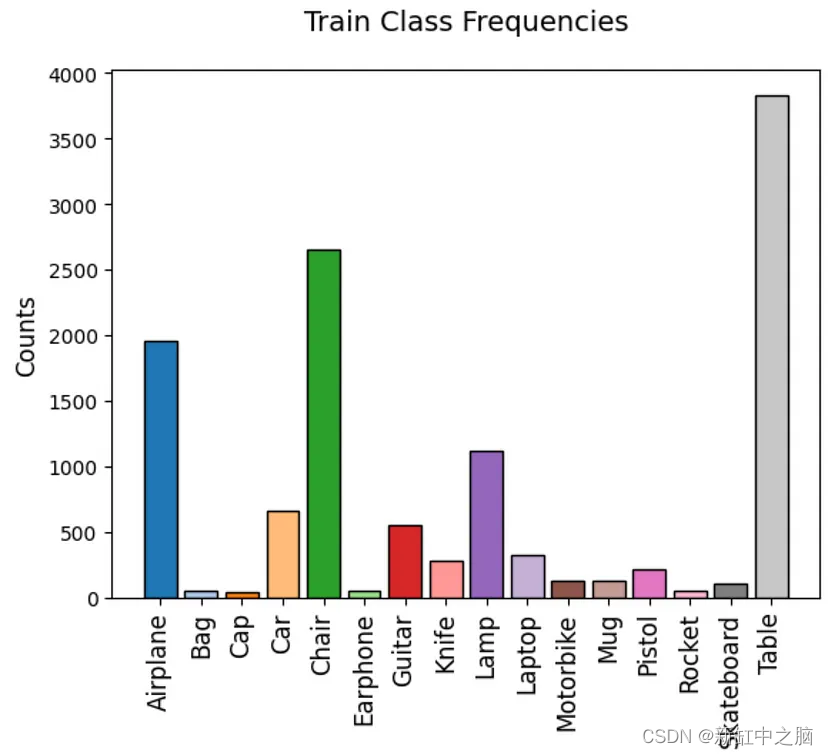
图 2. 训练分类数据点直方图
从图2中我们可以看出,这绝对不是一个平衡的训练集。 因此,我们可能想要应用类别权重,甚至使用焦点损失来帮助我们的模型学习。
3、PointNet损失函数
当训练PointNet进行分类时,我们可以使用 PyTorch 中的标准交叉熵损失,但我们还想添加包括论文中提到的正则化项。
正则化项强制特征变换矩阵正交,但为什么呢? 特征变换矩阵旨在旋转(变换)点云的高维表示。 我们如何确定这种学习的高维旋转实际上是在旋转点云? 为了回答这个问题,让我们考虑一些所需的旋转属性。
我们希望学习到的旋转是仿射的,这意味着它保留结构。 我们希望确保它不会做一些奇怪的事情,例如将其映射回较低维度的空间或弄乱结构。 我们不能只绘制 nx64 点云来检查这一点,但我们可以通过鼓励旋转正交来让模型学习有效的旋转。 这是因为正交矩阵同时保留长度和角度,而旋转矩阵是一种特殊类型的正交矩阵 。 我们可以“鼓励”模型通过使用以下项进行正则化来学习正交旋转矩阵:
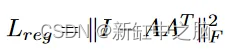
图 3.PointNet正则化项
我们利用正交矩阵的一个基本属性,即它们的列和行是正交向量。 对于完全正交的矩阵,图 3 中的正则化项将等于 0。
在训练期间,我们只需将此项添加到我们的损失中。 如果你已经完成了之前关于如何编码PointNet的教程,可能还记得特征转换矩阵 A 由分类头返回。
现在让我们编写PointNet损失函数的代码。 我们已经添加了加权(平衡)交叉熵损失和焦点损失的术语,但解释它们超出了本教程的范围。 其代码位于此处。 该代码改编自这个Github库。
import numpy as np
import torch
import torch.nn as nn
import torch.nn.functional as Fclass PointNetLoss(nn.Module):def __init__(self, alpha=None, gamma=0, reg_weight=0, size_average=True):super(PointNetLoss, self).__init__()self.alpha = alphaself.gamma = gammaself.reg_weight = reg_weightself.size_average = size_average# sanitize inputsif isinstance(alpha,(float, int)): self.alpha = torch.Tensor([alpha,1-alpha])if isinstance(alpha,(list, np.ndarray)): self.alpha = torch.Tensor(alpha)# get Balanced Cross Entropy Lossself.cross_entropy_loss = nn.CrossEntropyLoss(weight=self.alpha)def forward(self, predictions, targets, A):# get batch sizebs = predictions.size(0)# get Balanced Cross Entropy Lossce_loss = self.cross_entropy_loss(predictions, targets)# reformat predictions and targets (segmentation only)if len(predictions.shape) > 2:predictions = predictions.transpose(1, 2) # (b, c, n) -> (b, n, c)predictions = predictions.contiguous() \.view(-1, predictions.size(2)) # (b, n, c) -> (b*n, c)# get predicted class probabilities for the true classpn = F.softmax(predictions)pn = pn.gather(1, targets.view(-1, 1)).view(-1)# get regularization termif self.reg_weight > 0:I = torch.eye(64).unsqueeze(0).repeat(A.shape[0], 1, 1) # .to(device)if A.is_cuda: I = I.cuda()reg = torch.linalg.norm(I - torch.bmm(A, A.transpose(2, 1)))reg = self.reg_weight*reg/bselse:reg = 0# compute loss (negative sign is included in ce_loss)loss = ((1 - pn)**self.gamma * ce_loss)if self.size_average: return loss.mean() + regelse: return loss.sum() + reg
4、训练PointNet用于分类
现在我们已经了解了数据和损失函数,我们可以继续进行训练。
对于我们的训练需要量化模型的表现。 通常我们会考虑损失和准确性,但对于这个分类问题,我们需要一个衡量错误分类和正确分类的指标。 想想典型的混淆矩阵:真阳性、假阴性、真阴性和假阳性; 我们想要一个在所有这些方面都表现良好的分类器。
马修斯相关系数 (MCC) 量化了我们的模型在所有这些指标上的表现,并且被认为是比准确性或 F1 分数更可靠的单一性能指标。 MCC 的范围从 -1 到 1,其中 -1 是最差的性能,1 是最好的性能,0 是随机猜测。 我们可以通过 torchmetrics 将 MCC 与 PyTorch 结合使用。
from torchmetrics.classification import MulticlassMatthewsCorrCoefmcc_metric = MulticlassMatthewsCorrCoef(num_classes=NUM_CLASSES).to(DEVICE)
训练过程是一个基本的 PyTorch 训练循环,在训练和验证之间交替。
我们使用 Adam 优化器和我们的点净损失函数以及上面图 3 中描述的正则化项。对于点净损失函数,我们选择设置 alpha,它对每个样本的重要性进行加权。
我们还设置了 gamma 来调节损失函数并迫使其专注于困难示例,其中困难示例是那些以较低概率分类的示例。 有关更多详细信息,请参阅笔记本中的注释。 人们注意到,使用循环学习率时模型训练得更好,因此我们在这里实现了它。
import torch.optim as optim
from point_net_loss import PointNetLossEPOCHS = 50
LR = 0.0001
REG_WEIGHT = 0.001 # manually downweight the high frequency classes
alpha = np.ones(NUM_CLASSES)
alpha[0] = 0.5 # airplane
alpha[4] = 0.5 # chair
alpha[-1] = 0.5 # tablegamma = 1optimizer = optim.Adam(classifier.parameters(), lr=LR)
scheduler = torch.optim.lr_scheduler.CyclicLR(optimizer, base_lr=0.0001, max_lr=0.01, step_size_up=2000, cycle_momentum=False)
criterion = PointNetLoss(alpha=alpha, gamma=gamma, reg_weight=REG_WEIGHT).to(DEVICE)classifier = classifier.to(DEVICE)
请按照笔记本进行训练循环,并确保你有 GPU。 如果没有,请删除调度程序并将学习率设置为 0.01,几个 epoch 后你应该会得到足够好的结果。 如果遇到任何 PyTorch 用户警告(由于 nn.MaxPool1D 的未来更新),可以通过以下方式抑制它们:
import warnings
warnings.filterwarnings("ignore")
5、训练结果
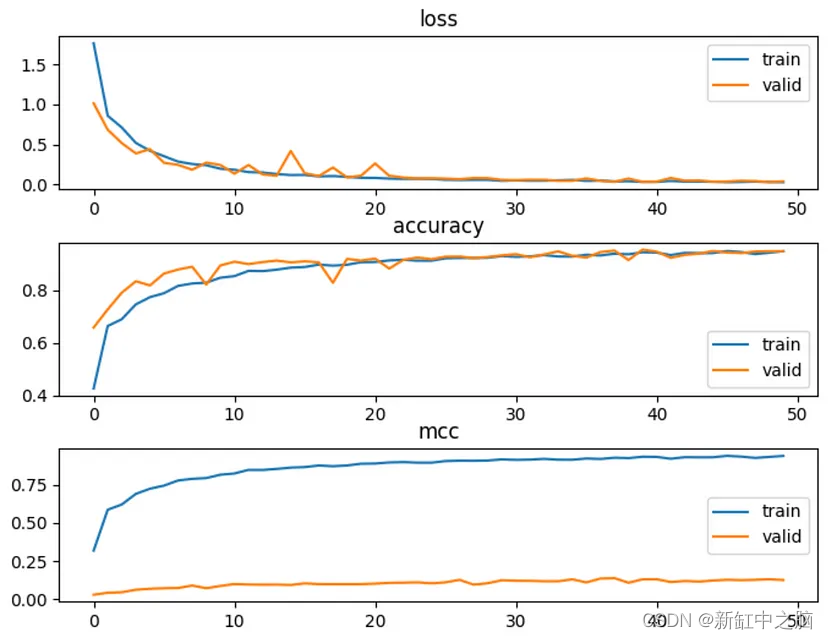
我们可以看到,训练和验证的准确率都上升了,但 MCC 仅在训练时上升,而在验证时却没有上升。 这可能是由于验证和测试分组中某些类的样本量非常小造成的; 因此在这种情况下,MCC 可能不是用于验证和测试的最佳单一指标。 这需要更多的调查来确定 MCC 何时是一个好的指标; 即多少不平衡对于 MCC 来说是过多? 每个类别需要多少样本才能使 MCC 有效?
我们来看看测试结果:

我们看到测试准确度约为 85%,但 MCC 略高于 0。由于我们只有 16 个类,让我们查看笔记本中的混淆矩阵,以更深入地了解测试结果。
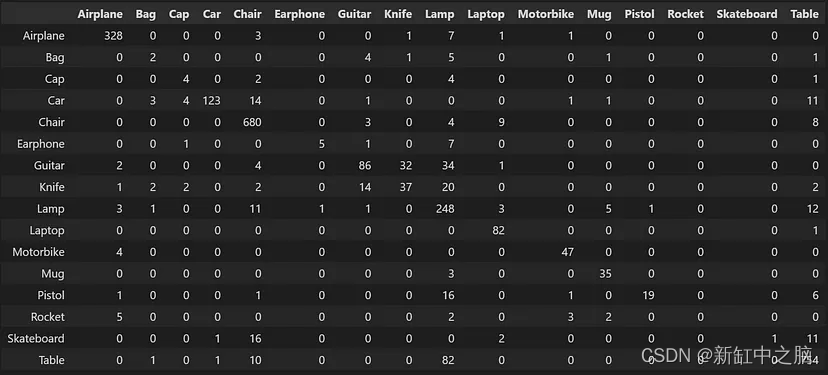
图 6. 测试数据混淆矩阵。 资料来源:作者。
大多数情况下,分类是可以的,但也有一些不太常见的类别,例如“火箭”或“滑板”。 该模型在这些类别上的预测性能往往较差,而在这些不太常见的类别上的性能是导致 MCC 下降的原因。
另一件需要注意的事情是,当你检查结果(如笔记本中所示)时,将在更频繁的分类中获得良好的准确性和自信的表现。 然而,在频率较低的课程中,你会发现置信度较低且准确性较差。
6、检查关键集
现在我们将研究本教程中最有趣的部分,即关键集。 关键集是点云集的基本基础点。 这些点定义了它的基本结构。 这里有一些代码展示了如何可视化它们。
from open3d.web_visualizer import draw critical_points = points[crit_idxs.squeeze(), :]
critical_point_colors = read_pointnet_colors(seg.numpy())[crit_idxs.cpu().squeeze(), :]pcd = o3.geometry.PointCloud()
pcd.points = o3.utility.Vector3dVector(critical_points)
pcd.colors = o3.utility.Vector3dVector(critical_point_colors)# o3.visualization.draw_plotly([pcd])
draw(pcd, point_size=5) # does not work in Colab
这里有一些可视化,请注意,我使用“draw()”来获得更大的点大小,但它在 Colab 中不起作用。

图 7.点云集及其由PointNet学习的相应关键集
我们可以看到,关键集展示了其对应点云的整体结构,它们本质上是稀疏采样的点云。 这表明训练后的模型实际上已经学会了区分差异结构,并表明它实际上能够根据每个点云类别的区别结构对其进行分类。
7、结束语
我们学习了如何从头开始训练PointNet以及如何可视化点集。 如果你真的感兴趣,请尝试提高整体分类性能。 以下是一些帮助你入门的建议:
- 使用不同的损失函数
- 在循环学习率调度程序中尝试不同的设置
- 尝试对PointNet架构进行修改
- 尝试不同的数据增强
- 使用更多数据 → 尝试完整的 shapenet 数据集
原文链接:PointNet分类3D点云 — BimAnt