【高级程序设计语言C++】红黑树

  • 1. 红黑树的概念
  • 2. 红黑树的插入
    • 2.1. 情况1
    • 2.2. 情况2
    • 2.3. 情况3
    • 2.4. 插入情况小总结
  • 3. 红黑树与AVL树的对比
  • 4. 红黑树在线生成网站

1. 红黑树的概念

红黑树（Red-Black Tree）是一种自平衡的二叉搜索树，它在插入和删除操作时通过调整节点的颜色和旋转来保持树的平衡。红黑树的平衡性是通过以下规则来定义和维护的：

  1. 每个节点要么是红色，要么是黑色。
  2. 根节点是黑色。
  3. 每个叶子节点（NIL节点，空节点）都是黑色。
  4. 如果一个节点是红色的，则它的两个子节点都是黑色的。
  5. 对于每个节点，从该节点到其所有后代叶子节点的简单路径上，均包含相同数目的黑色节点（称为黑色高度）。

通过这些规则，红黑树能够保持相对平衡，从而保证了其插入、删除和查找等操作的时间复杂度都能够保持在O(log n)级别。

红黑树图：

img

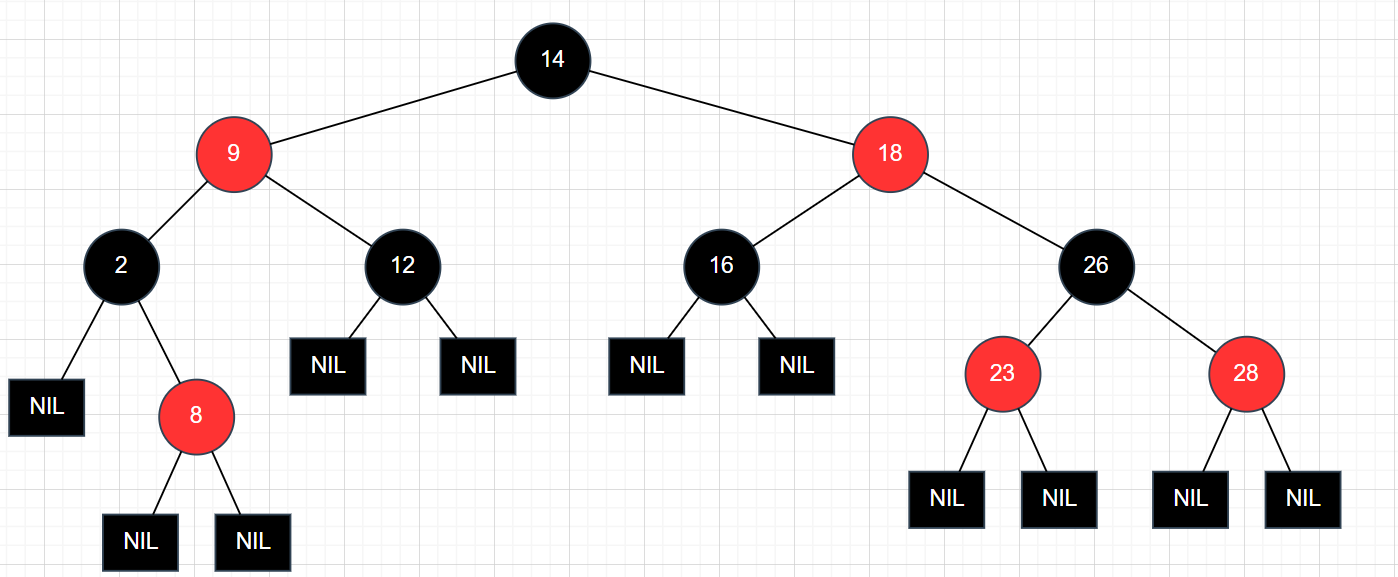
关于性质的说明：

  1. 不可能出现连续两个红节点

img

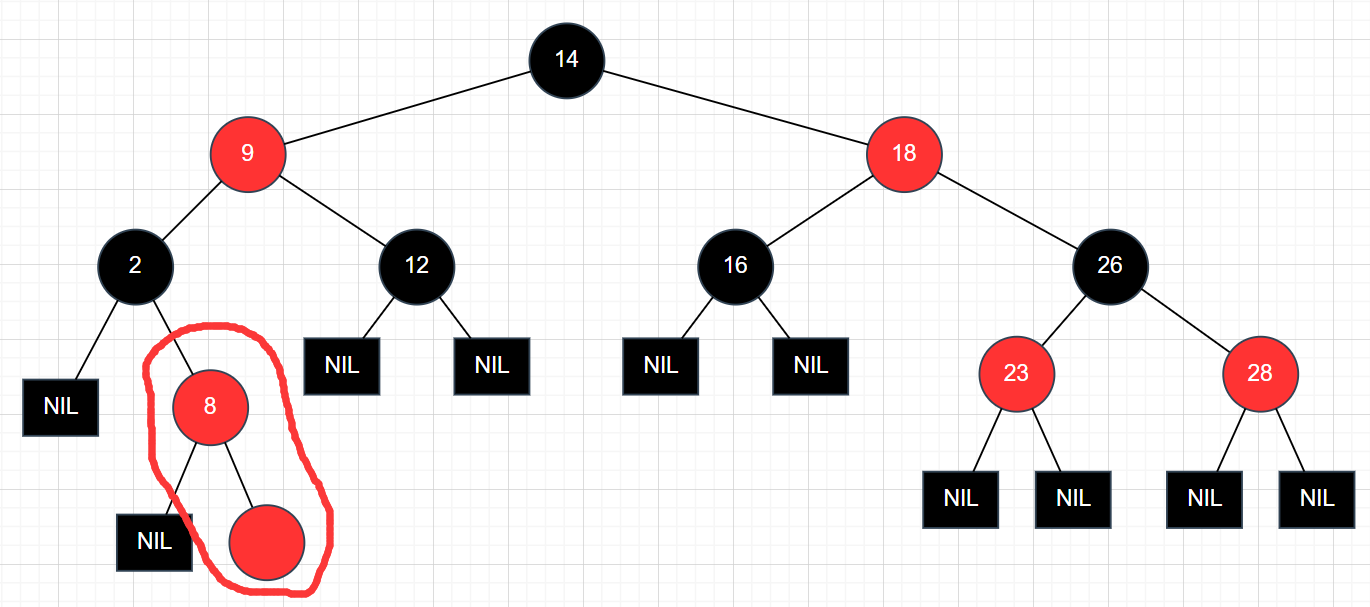
这种情况是不允许的！

  1. 每条路径上的黑色节点数是相同的。

img

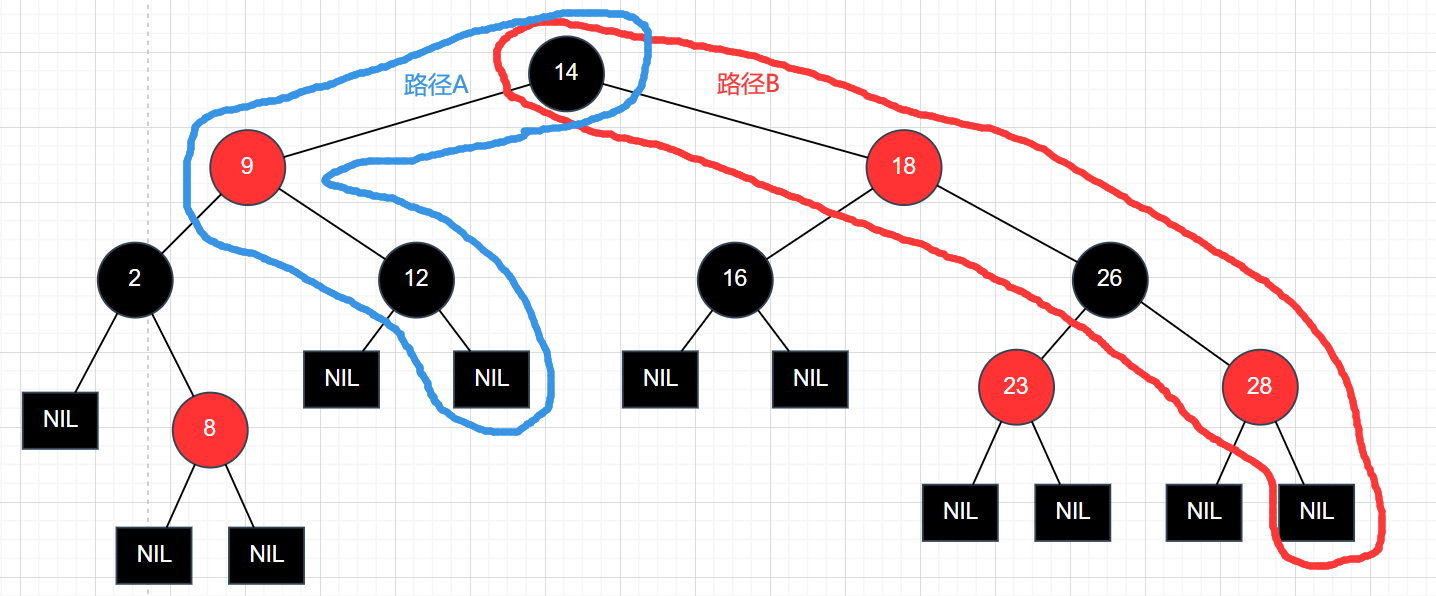
如图中的路径A与路径B，他们黑色节点数是相同的，如果违背了这些性质，红黑树的结构将会被破坏。

2. 红黑树的插入

红黑树本身是二叉搜索树，只不过是在其基础增加了颜色的区分。所以插入是跟二叉搜索树一样的，不过要根据红黑树的规则来调整。

插入大概上分为3种情况：

2.1. 情况1

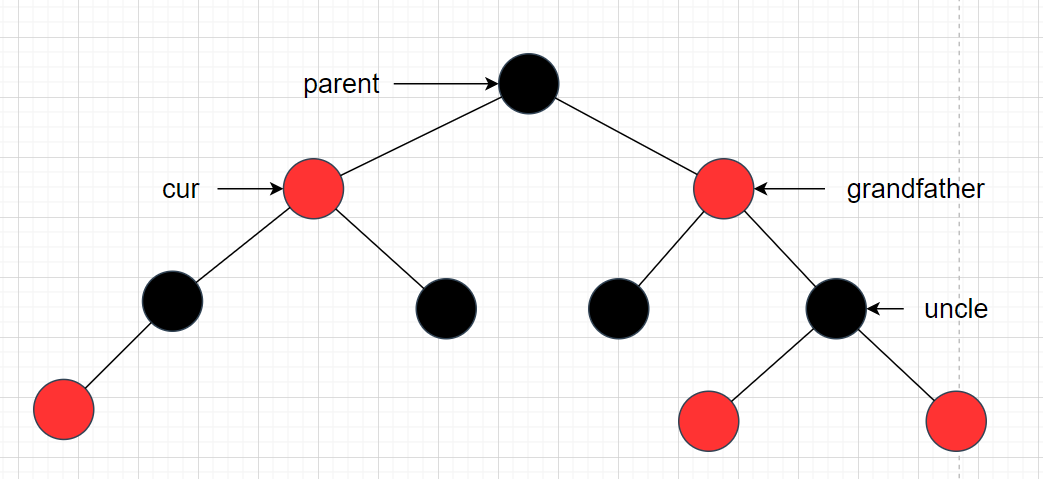
cur为红，p为红，g为黑，u存在且为红

举个简单例子，如图：

img

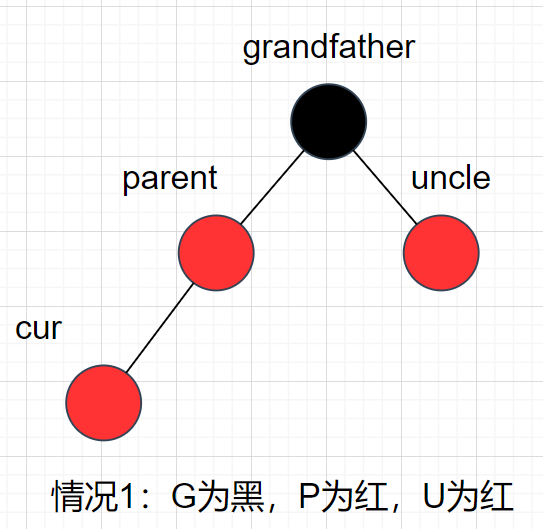
这种情况违背了红黑树的规则，有两个连续的红节点，此时就需要调整。

  1. 把parent和uncle变为黑色
  2. 再把grandfather变为红色
  3. 把grandfa给给cur，再继续往上看是否需要调整

调整后的红黑树：

img

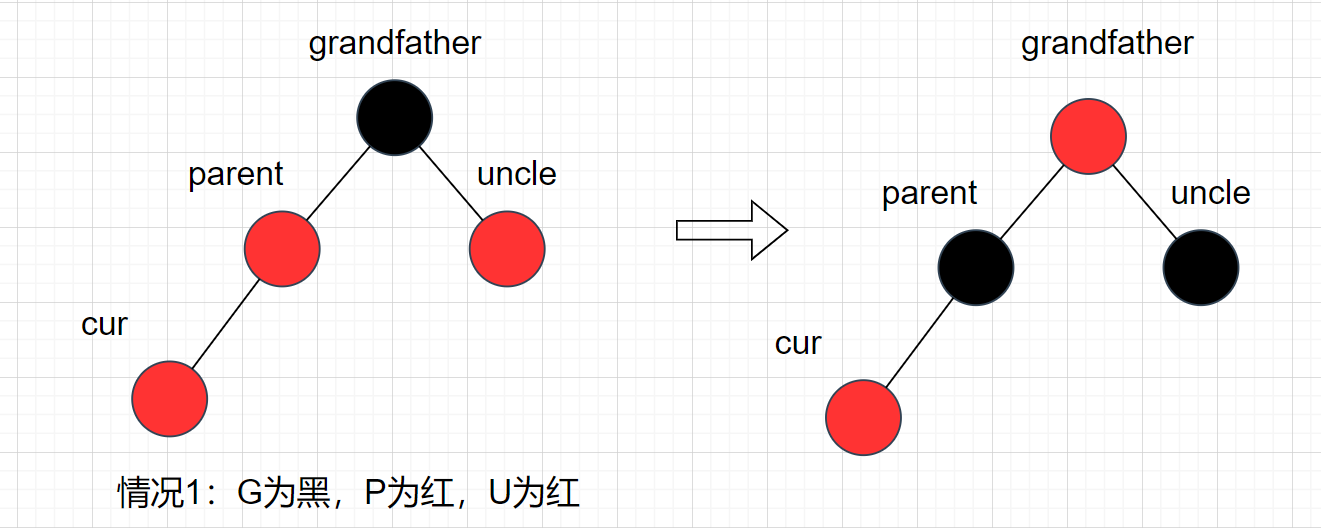
根据上面的情况分析给出抽象图：

img

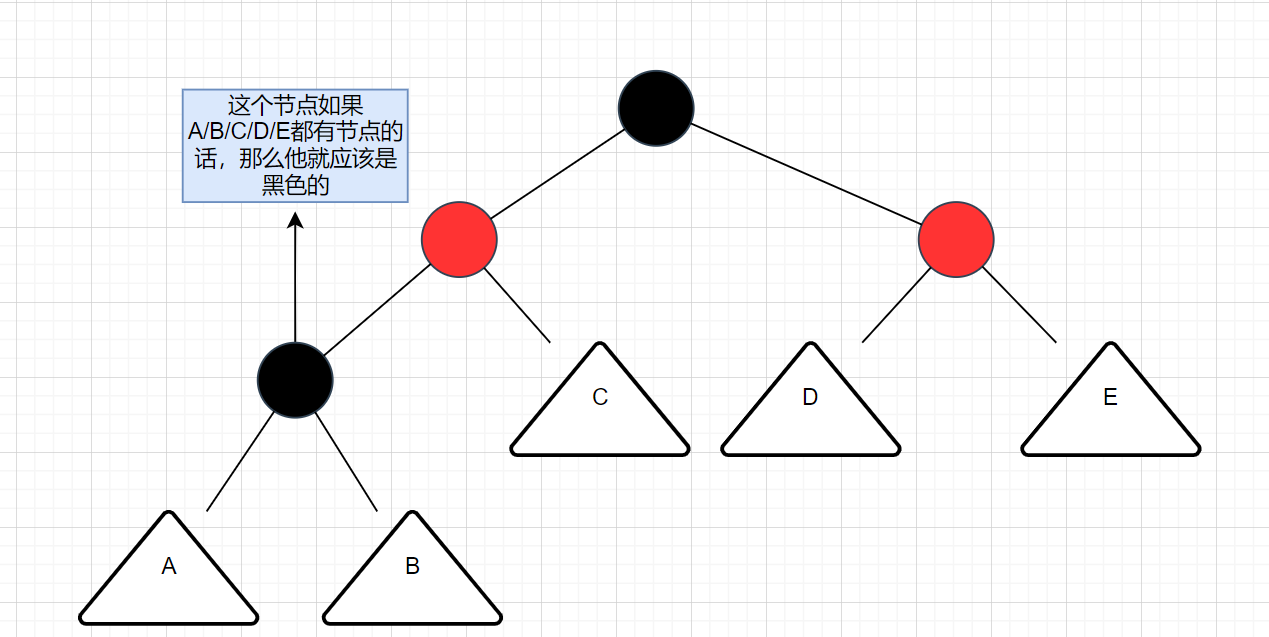
**假设A/B/C/D/E为一个节点，那么C/D/E的节点将会是黑色的，而A/B是红色的。**具体为什么可以参考红黑树的规则想想。

如果此时选择插入一个节点，那么将会出现情况1。

那么此时具体图如下：

img

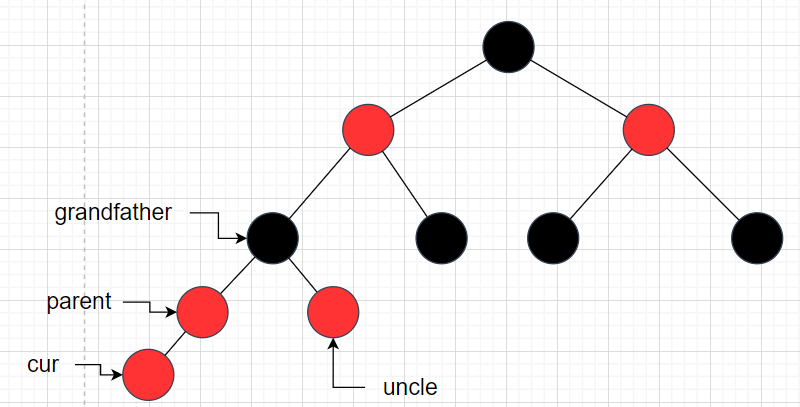
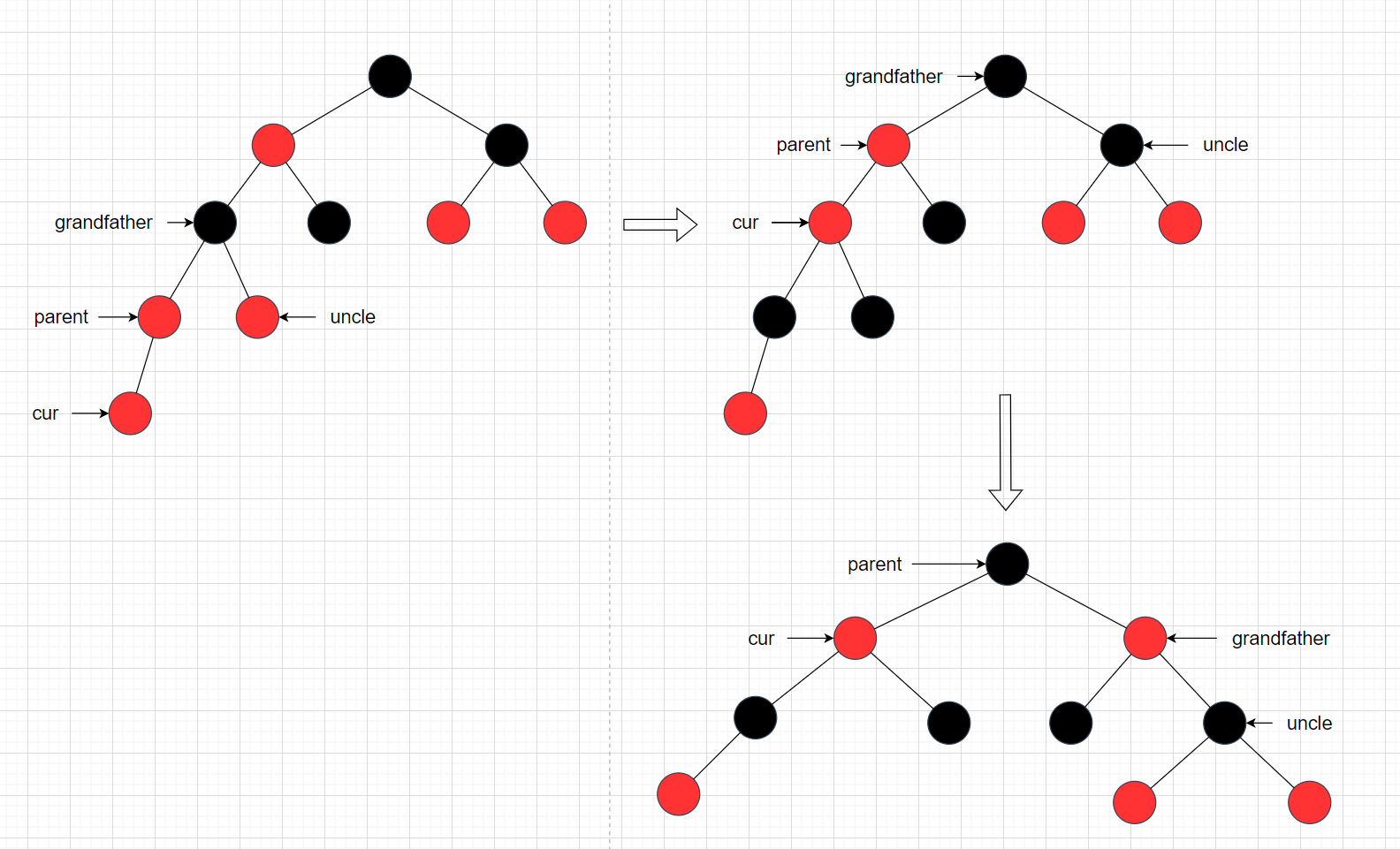
第一次调整如图：

img

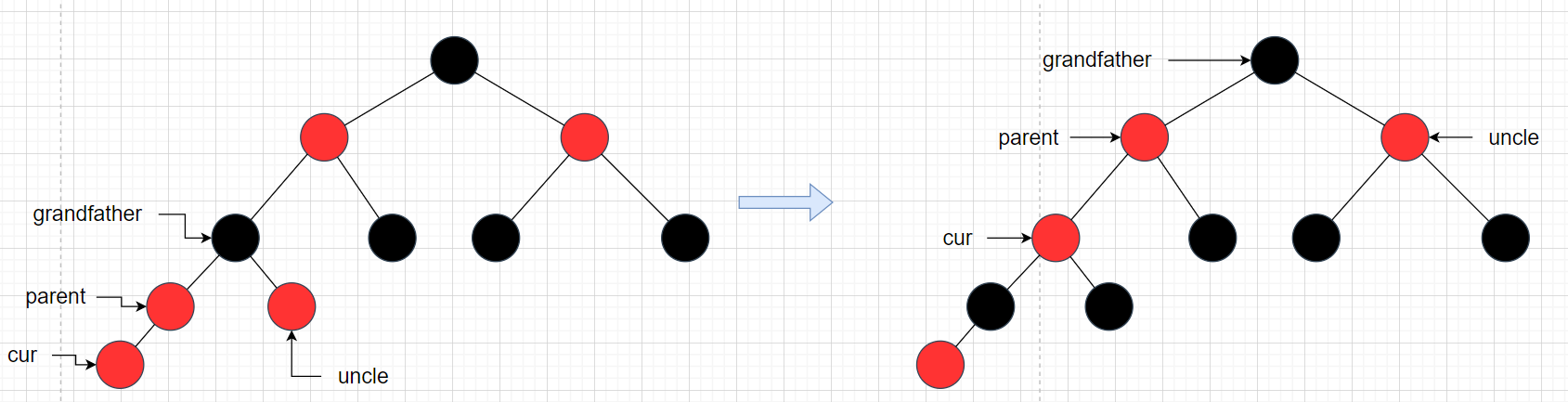
第一次调整结束后，根据调整过程cur会变动，根据情况分析，此时还需要再一次调整。

第二次调整：

img

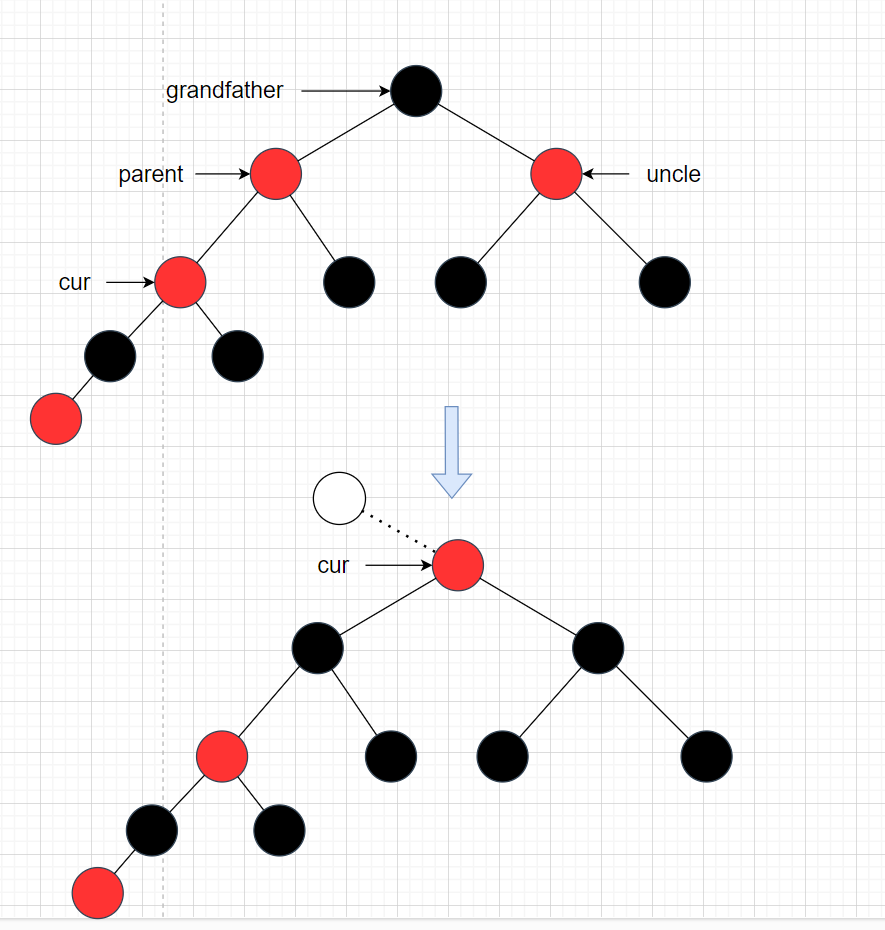
此时白色圆圈代表的是，这棵树可能只是一颗子树，如果不是子树的的话，根节点的颜色要变黑色。

img

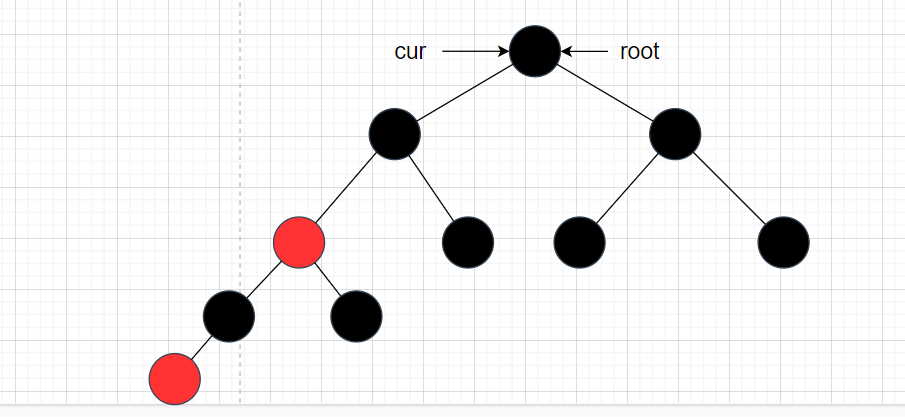
根据抽象图来画具象图，会有很多种情况，但最主要的情况就是cur为红，p为红，g为黑，u存在且为红.

代码如下：

img

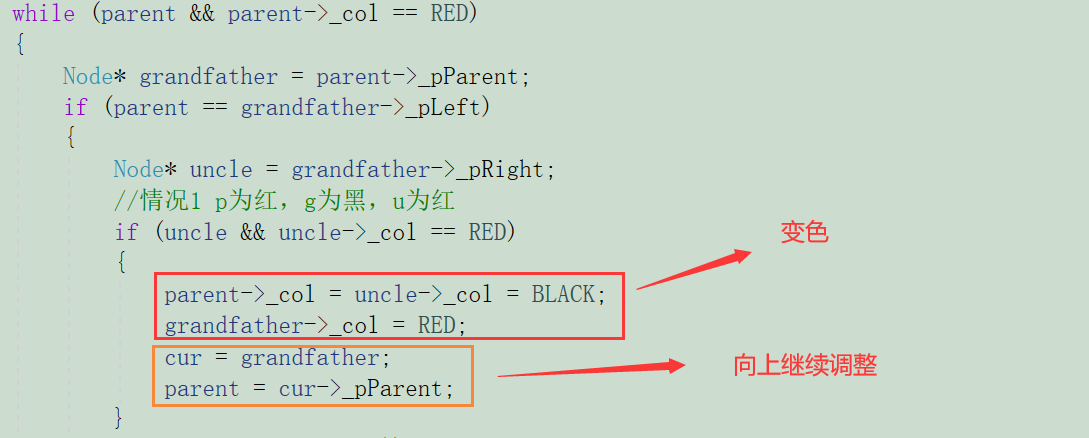
2.2. 情况2

cur红且为p左子树，p为红，g为黑，u不存在/u存在且为黑

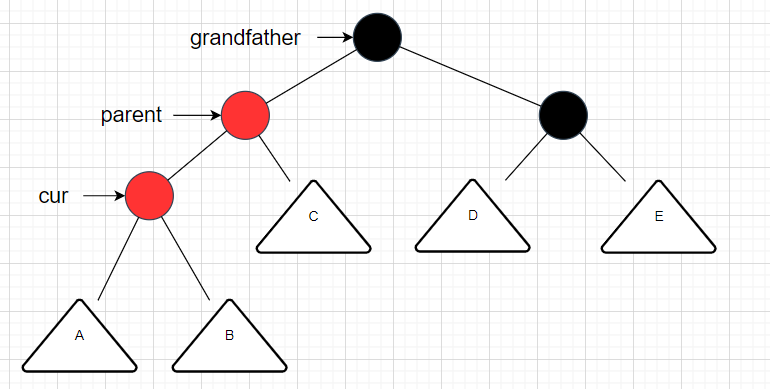
先举抽象图例子：

img

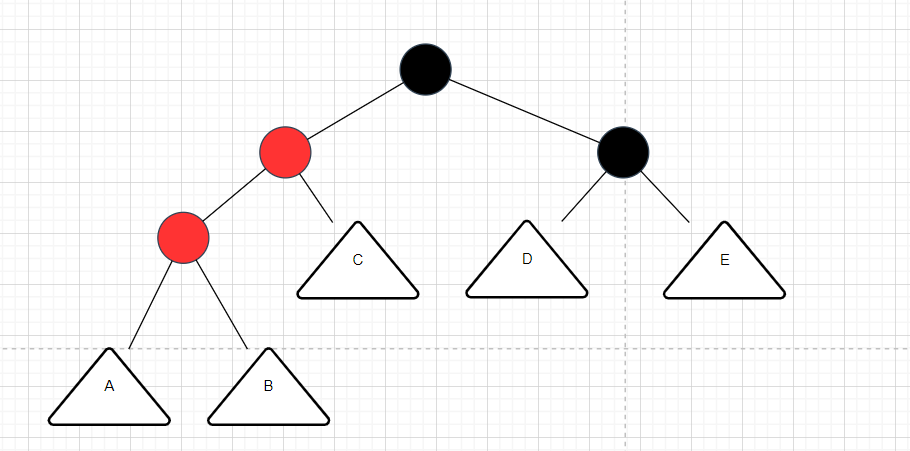
当A/B/C/D/E都为空的时候，那么uncle节点是不可能存在的。**因为如果uncle此时存在的话，那么就是情况1，但这里讨论的是情况2，情况2要求的是uncle节点要么存在，要么不存在，而如果uncle存在的话，将不符合红黑树结构的要求。**具象图如下：

img

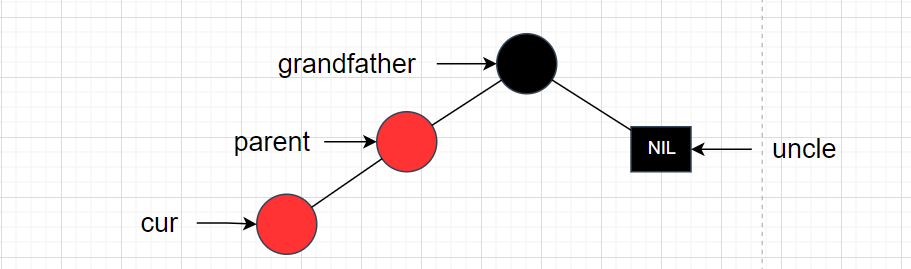
那么此时就是情况2的uncle节点不存在的情况。所需要做的就是进行右单旋操作。调整后如下图：

img

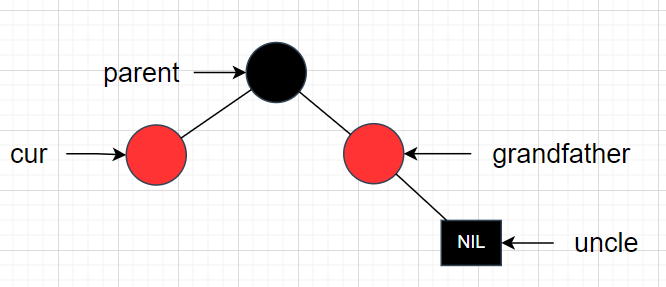
为什么旋转之后，颜色是这样子变化呢？我想要cur和grandfather的颜色为黑，parent为红不行吗？别急，答案在抽象图会出来。

当A/B/C/D/E的高度为1，并且cur节点的颜色为黑色，如下图所示：

img

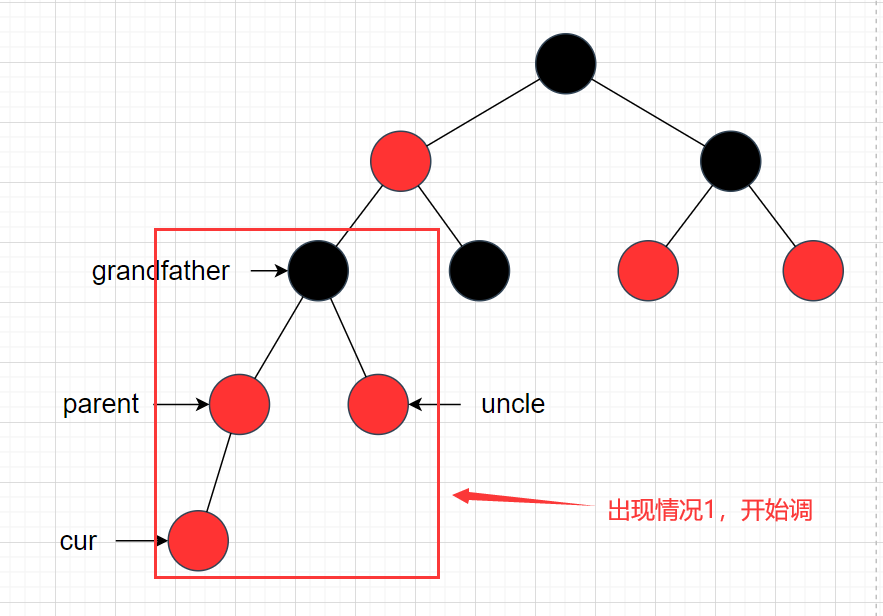
调整后如下图：

img

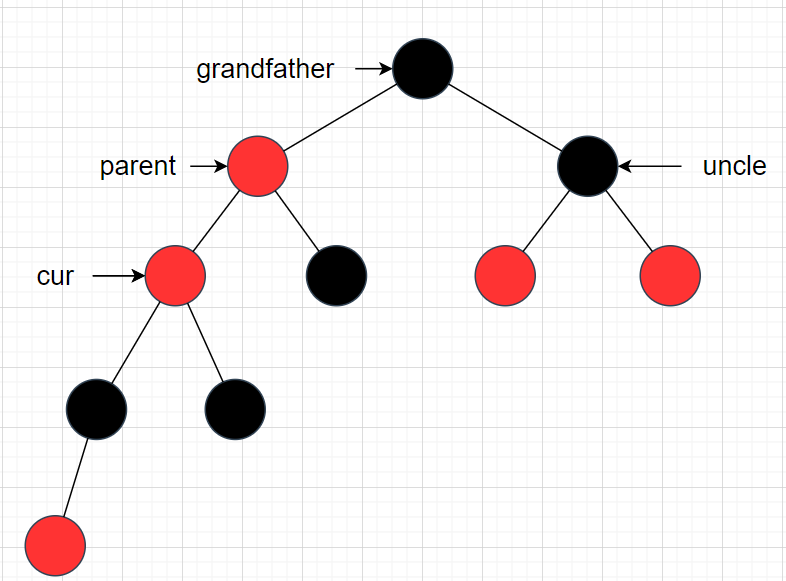
此时这种情况就是情况2，要进行旋转，旋转后如下图：

img

总体的旋转如下图所示：

img

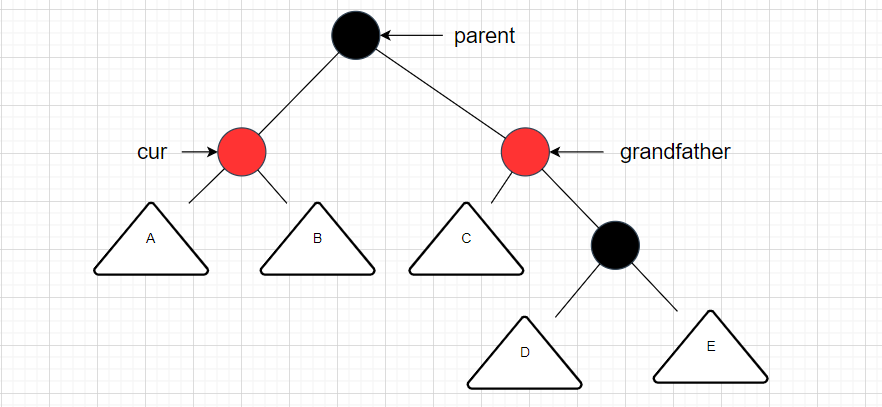
情况2的抽象图：

img

经过旋转，但是颜色未变的视图：

img

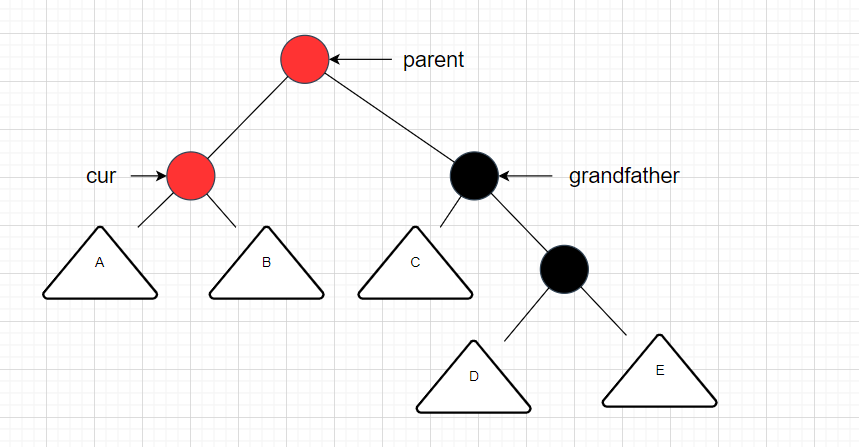
如上图所见，这里的grandfather节点颜色是不能为黑色的，因为不符合红黑树的结构规则，因此是要将grandfather和cur的颜色变为红色，而parent颜色为黑色，如下图所示：

img

代码如下：

img

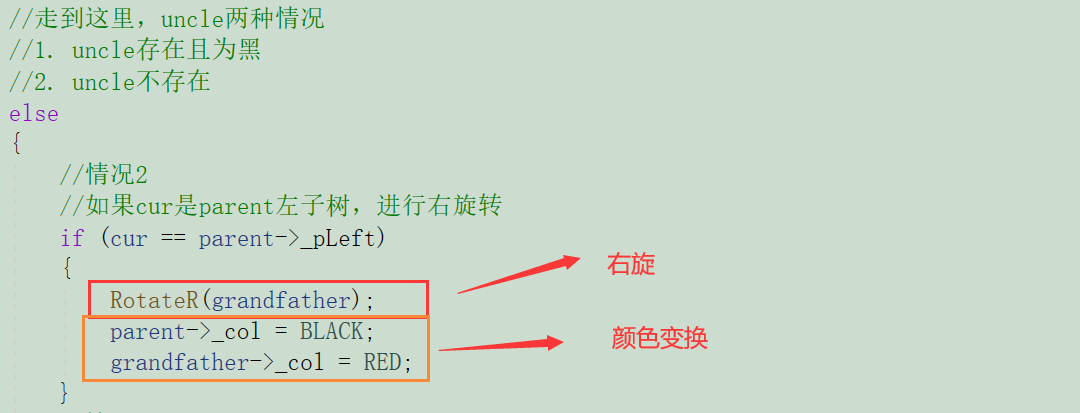
2.3. 情况3

cur红且为p右子树，p为红，g为黑，u不存在/u存在且为黑

这里只画A/B/C/D/E为一个节点时的具象图。

img

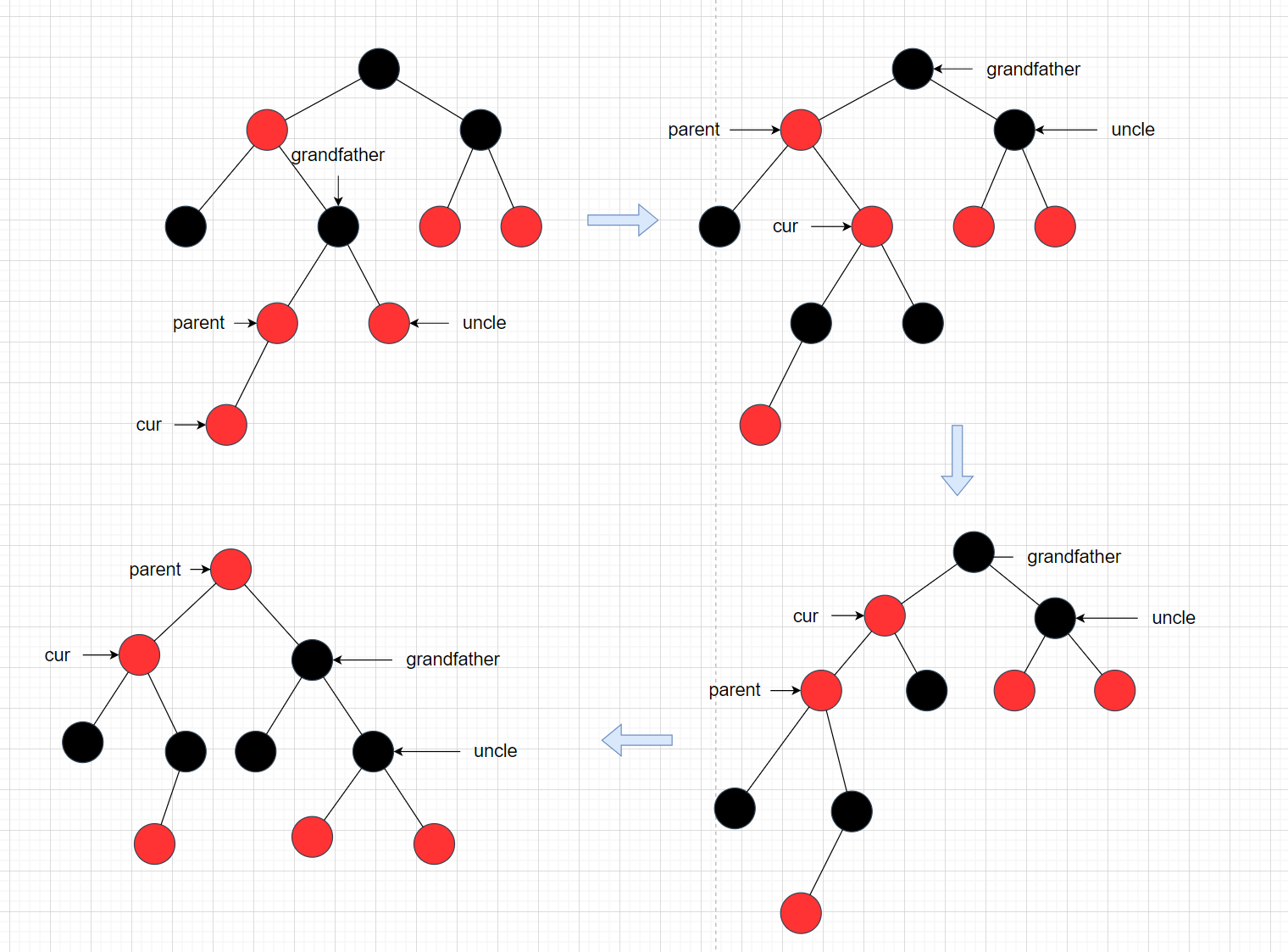
具体来说就是，当A/B/C/D/E高度为1的时候，先是碰到了情况1，调整之后，变成了情况2，再调整后，又变成了另一个方向的情况2。那么就根据这种种情况，依次旋转即可。

代码如下：

img

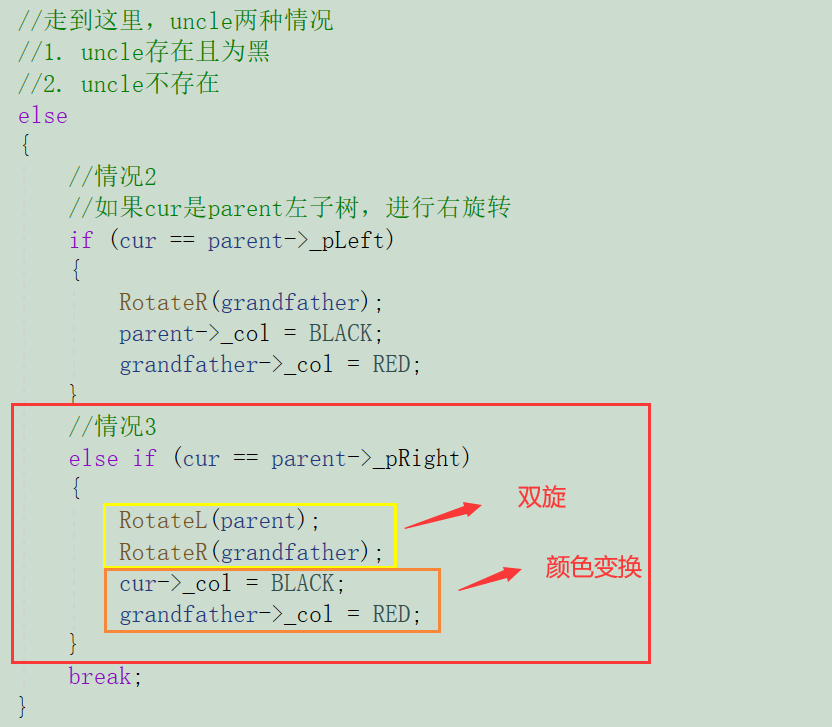
最后要记得把根节点的颜色变为黑色：

img

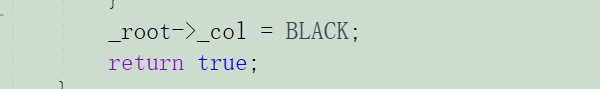
代码实现：

bool Insert(const T& data){if (_root == nullptr){_root = new Node(data);_root->_col = BLACK;return true;}Node* cur = _root;Node* parent = nullptr;while (cur){if (data > cur->_data){parent = cur;cur = cur->_pRight;}else if (data < cur->_data){parent = cur;cur = cur->_pLeft;}else{return false;}}cur = new Node(data);if (data > parent->_data){parent->_pRight = cur;cur->_pParent = parent;}else if (data < parent->_data){parent->_pLeft = cur;cur->_pParent = parent;}//新插入的节点默认颜色为红色，所以下面cur颜色都为红while (parent && parent->_col == RED){Node* grandfather = parent->_pParent;if (parent == grandfather->_pLeft){Node* uncle = grandfather->_pRight;//情况1 p为红，g为黑，u为红if (uncle && uncle->_col == RED){parent->_col = uncle->_col = BLACK;grandfather->_col = RED;cur = grandfather;parent = cur->_pParent;}//走到这里，uncle两种情况//1. uncle存在且为黑//2. uncle不存在else{//情况2//如果cur是parent左子树，进行右旋转if (cur == parent->_pLeft){RotateR(grandfather);parent->_col = BLACK;grandfather->_col = RED;}//情况3else if (cur == parent->_pRight){RotateL(parent);RotateR(grandfather);cur->_col = BLACK;grandfather->_col = RED;}break;}}else if (parent == grandfather->_pRight){Node* uncle = grandfather->_pLeft;//情况1 p为红，g为黑，u为红if (uncle && uncle->_col == RED){parent->_col = uncle->_col = BLACK;grandfather->_col = RED;cur = grandfather;parent = cur->_pParent;}//走到这里，uncle两种情况//1. uncle存在且为黑//2. uncle不存在else{//情况2//如果cur是parent左子树，进行右旋转if (cur == parent->_pLeft){RotateR(parent);RotateL(grandfather);cur->_col = BLACK;grandfather->_col = RED;}//情况3else if (cur == parent->_pRight){RotateL(grandfather);parent->_col = BLACK;grandfather->_col = RED;}break;}}}_root->_col = BLACK;return true;}

2.4. 插入情况小总结

  1. 大类上分为两类，一是uncle节点为红色，而是uncle节点为黑色
  2. 根据uncle节点的颜色，又分为两种情况
  3. 如果uncle节点颜色为红色，并且parent节点和cur节点都为红色，那么就是情况1，直接变颜色即可
  4. 如果uncle节点颜色为黑色，并且parent节点和cur节点都为红色，cur是parent的左节点，那么就是情况2，单旋转
  5. 如果uncle节点颜色为黑色，并且parent节点和cur节点都为红色，cur是parent的右节点，那么就是情况3，双旋转
  6. 关键就是看uncle节点是否存在以及uncle节点的颜色

3. 红黑树与AVL树的对比

红黑树和AVL树都是常用的自平衡二叉搜索树，它们的主要目的都是为了保持树的平衡，以提高搜索、插入和删除操作的性能。然而，红黑树和AVL树在平衡的方式和性能方面存在一些差异。

  1. 平衡性：
    • 红黑树：红黑树通过在节点上引入颜色属性，并遵循一组平衡规则来保持平衡。这些规则包括节点的颜色、路径上的黑色节点数量等。红黑树的平衡性相对较弱，可以在维护平衡的同时提供较高的插入和删除性能。
    • AVL树：AVL树通过在节点上维护一个平衡因子（左子树高度减去右子树高度）来保持平衡。AVL树的平衡性相对较强，要求任何节点的平衡因子在-1、0、1之间。这种强平衡性保证了AVL树的高度始终保持在较小的范围内，但可能会导致插入和删除操作的性能稍低。
  1. 插入和删除操作：
    • 红黑树：由于红黑树的平衡性相对较弱，插入和删除操作的性能较好。红黑树在执行这些操作时只需要进行一些颜色调整和旋转操作，时间复杂度为O(log n)。
    • AVL树：由于AVL树的平衡性较强，插入和删除操作可能需要进行更多的旋转操作来保持平衡，因此性能略低于红黑树。插入和删除操作的时间复杂度为O(log n)。
  1. 查询操作：
    • 红黑树和AVL树在查询操作上的性能相似，时间复杂度为O(log n)。它们都具有快速的搜索能力，可以在平衡的树结构中进行高效的查找。
  1. 空间复杂度：
    • 红黑树和AVL树的空间复杂度都是O(n)，其中n是树中节点的数量。它们在每个节点上都需要存储额外的信息来维护平衡性。

综上所述，红黑树和AVL树在平衡性和性能方面存在一些差异。选择使用哪种树结构取决于具体应用场景和需求。如果插入和删除操作频繁且对性能要求较高，可以选择红黑树。如果对平衡性要求较高且能够容忍稍低的性能，可以选择AVL树。

4. 红黑树在线生成网站

如果想验证一组数据生成的红黑树是什么样子的，可以用这个网站去看看。这个网站也是从csdn大佬的博客中发现的，这里给大家链接，希望大佬们能够有所收获。

https://www.cs.usfca.edu/~galles/visualization/RedBlack.html

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.rhkb.cn/news/81214.html

如若内容造成侵权/违法违规/事实不符，请联系长河编程网进行投诉反馈email:809451989@qq.com，一经查实，立即删除！

相关文章

Scrum是什么意思，Scrum敏捷项目管理工具有哪些？

Scrum是什么意思，Scrum敏捷项目管理工具有哪些？

一、什么是Scrum&#xff1f; Scrum是一种敏捷项目管理方法&#xff0c;旨在帮助团队高效地开展软件开发和项目管理工作。 Scrum强调迭代和增量开发&#xff0c;通过将项目分解为多个短期的开发周期&#xff08;称为Sprint&#xff09;&#xff0c;团队可以更好地应对需求变…
阅读更多...
FFmpeg常见命令行（二）：FFmpeg转封装

FFmpeg常见命令行（二）：FFmpeg转封装

前言 在Android音视频开发中&#xff0c;网上知识点过于零碎&#xff0c;自学起来难度非常大&#xff0c;不过音视频大牛Jhuster提出了《Android 音视频从入门到提高 - 任务列表》。本文是Android音视频任务列表的其中一个&#xff0c; 对应的要学习的内容是&#xff1a;如何使…
阅读更多...
HttpRunner自动化测试之脚手架工具使用(一键搭建)

HttpRunner自动化测试之脚手架工具使用(一键搭建)

脚手架工具使用&#xff1a; 每一个成熟的系统工具&#xff0c;都会有对应的脚手架工具&#xff0c;它可以快速构建项目的必要目录&#xff0c;不必自己一个一个的配置与搭建&#xff0c;只需要执行一些命令即可。 httprunner也提供了脚手架工具&#xff0c;使用步骤如下&…
阅读更多...
通过Idea部署Tomcat服务器（详细图文教学）

通过Idea部署Tomcat服务器（详细图文教学）

1.在idea中创建项目 有maven构建工具就创建maven&#xff0c;没有就正常创建一个普通的java程序 创建普通java项目 2.添加框架 3.配置 Tomcat 注意&#xff1a;创建web项目后我们需要配置tomcat才能运行&#xff0c;下面我们来进行配置。 4.添加部署 回到服务器 5.完善配置 6…
阅读更多...
Excel表格(一)

Excel表格(一)

1.单一栏的宽度和高度设置 2.大标题的跨栏居中 3.让单元格内的文字------自动适应 4.序号递增 5.货币符号 6.日期格式的选择 选到单元格&#xff0c;选中对应的日期格式 7.自动求和的计算 然后在按住回车键即可求出当前行的金额 点击自动求和 8.冻结表格栏 9.排序 1.单栏排序 …
阅读更多...
【redis】SpringBoot集成redis

【redis】SpringBoot集成redis

目录 1.添加redis依赖2.配置redis3.操作redis3.1 操作string 3.1 操作其它数据类型 4. Spring-Session基于Redis解决共享Session问题4.1 问题提出 4.1 添加依赖 4.2 修改配置4.3 存储和读取 1.添加redis依赖 方法①&#xff1a; <dependency><groupId>org.springf…
阅读更多...
WordPress 子主题（child theme）介绍

WordPress 子主题（child theme）介绍

经常开发WordPress主题的朋友往往会遇到一个困惑&#xff0c;虽然主题提供了默认设置&#xff0c;也自带了不少自定义功能&#xff0c;可以满足大部分的场景使用&#xff0c;但毕竟众口难调&#xff0c;一些个性化的需求难免无法满足&#xff0c;这时就必须得修改主题文件来实现…
阅读更多...
【动态规划刷题 5】 最小路径和地下城游戏

【动态规划刷题 5】 最小路径和地下城游戏

最小路径和 链接: 64. 最小路径和 给定一个包含非负整数的 m x n 网格 grid &#xff0c;请找出一条从左上角到右下角的路径&#xff0c;使得路径上的数字总和为最小。 说明&#xff1a;每次只能向下或者向右移动一步。 输入&#xff1a;grid [[1,3,1],[1,5,1],[4,2,1]] 输…
阅读更多...
使用 PowerShell 将 Excel 中的每个工作表单独另存为独立的文件

使用 PowerShell 将 Excel 中的每个工作表单独另存为独立的文件

导语&#xff1a;在日常工作中&#xff0c;我们经常需要处理 Excel 文件。本文介绍了如何使用 PowerShell 脚本将一个 Excel 文件中的每个工作表单独另存为独立的 Excel 文件&#xff0c;以提高工作效率。 1. 准备工作 在开始之前&#xff0c;请确保已经安装了 Microsoft Exc…
阅读更多...
Cocos基本介绍

Cocos基本介绍

一、下载Dashboard Cocos Creator 3.8 手册 - 安装和启动 二、编辑器结构 1.资源管理器&#xff1a;显示了项目资源文件夹(assets)中的所有资源 2.场景编译器&#xff1a;用于展示和编辑场景中可是内容的工作区域 3.层级管理器&#xff1a;用树状列表的形式展示场景中的所有…
阅读更多...
pytest测试框架之fixture测试夹具详解

pytest测试框架之fixture测试夹具详解

fixture的优势 ​ pytest框架的fixture测试夹具就相当于unittest框架的setup、teardown&#xff0c;但相对之下它的功能更加强大和灵活。 命名方式灵活&#xff0c;不限于unittest的setup、teardown可以实现数据共享&#xff0c;多个模块跨文件共享前置后置可以实现多个模块跨…
阅读更多...
【AutoLayout案例1-按钮居中显示 Objective-C语言】

【AutoLayout案例1-按钮居中显示 Objective-C语言】

一、按钮居中显示 1.接下来，我们就用这个autoLayout，自动布局，给大家写一个，实现几个案例，给大家看一下 那么，首先，第一个，大家注意， 当我们使用autoLayout，自动布局的时候，我们新建一个项目， 这个新建的项目，里面有一个控制器，这个控制器，是不是默认，是四四…
阅读更多...
FreeRTOS通过消息队列实现串口命令解析（串口中断）

FreeRTOS通过消息队列实现串口命令解析（串口中断）

作者&#xff1a;Jack_G 时间&#xff1a;2023.08.08 版本&#xff1a;V1.0 上次修改时间&#xff1a; 环境&#xff1a; \quad \quad \quad \quad STM32Cube MX V6.8.1 \quad \quad \quad \quad STM32CubeH7 Firmware Package V1.11.0 / 04-Nov-2022 \quad \quad \quad \qu…
阅读更多...
创意项目管理软件推荐：满足客户需求的完美解决方案

创意项目管理软件推荐：满足客户需求的完美解决方案

发现功能强大的工作管理软件&#xff0c;让创意大放异彩。将您团队的愿景变成引人注目的项目。 一、交付总是令人印象深刻的工作 Zoho Projects的创意项目管理软件可帮助您和您的团队在一个地方监督多个项目。使用我们的内置管理工具和模板&#xff0c;花更少的时间在管理上&a…
阅读更多...
【福建事业单位-推理判断】02图形推理（数量-空间重构）

【福建事业单位-推理判断】02图形推理（数量-空间重构）

【福建事业单位-推理判断】02图形推理&#xff08;数量-空间重构&#xff09; 一、数量规律1.1点&#xff08;交点、切点&#xff09;点的细化考法总结 1.2线条&#xff08;线条的数量&#xff09;线的细化考点一笔画&#xff08;重点&#xff09;一笔画的判定 总结 1.3 面面的…
阅读更多...
Ajax同源策略及跨域问题

Ajax同源策略及跨域问题

Ajax同源策略及跨域问题 同源策略ajax跨域问题什么是跨域&#xff1f;为什么不允许跨域&#xff1f;跨域解决方案1、CORS2、express自带的中间件cors3、JSONP原生JSONPjQuery发送JSONP 4、使用vscode的Live Server插件 同源策略 同源策略&#xff08;Same-Origin Policy&#…
阅读更多...
数学建模学习（9）：模拟退火算法

数学建模学习（9）：模拟退火算法

模拟退火算法(Simulated Annealing, SA)的思想借 鉴于固体的退火原理&#xff0c;当固体的温度很高的时候&#xff0c;内能比 较大&#xff0c;固体的内部粒子处于快速无序运动&#xff0c;当温度慢慢降 低的过程中&#xff0c;固体的内能减小&#xff0c;粒子的慢慢趋于有序&a…
阅读更多...
华三H3C S5120V3交换机的配置之组建IRF

华三H3C S5120V3交换机的配置之组建IRF

IRF&#xff08;Intelligent Resilient Framework&#xff0c;智能弹性架构&#xff09;&#xff0c;是华三交换机实现虚拟堆叠的一种技术&#xff0c;其核心思想是将多台交换机连接在一起&#xff0c;虚拟成一台交换机&#xff0c;进而实现统一管理。和传统的堆叠概念不同&…
阅读更多...
HTML

HTML

HTML 1. 块级标签 标题&#xff1a; <h1>一级标题</h1> div: <div>这是一个div标签</div> p&#xff1a; <p>这是一个p标签&#xff0c;段落标签</p> <!DOCTYPE html> <html lang"en"> <head><meta charse…
阅读更多...
如何使用 ChatGPT 规划家居装修

如何使用 ChatGPT 规划家居装修

你正在计划家庭装修项目&#xff0c;但不确定从哪里开始&#xff1f;ChatGPT 随时为你提供帮助。从集思广益的设计理念到估算成本&#xff0c;ChatGPT 可以简化你的家居装修规划流程。在本文中&#xff0c;我们将讨论如何使用 ChatGPT 有效地规划家居装修&#xff0c;以便你的项…
阅读更多...
最新文章
推荐文章

Copyright @ 2022~2023