Problem - 7354

题目大意：有一棵n个点的树，A和B分别从点x，y开始，每轮可以移动到一个相邻节点，但如果某个节点有人访问过，则两人都不能访问那个节点，先没有点可走的人输，问A有没有必胜策略赢

2<=n<=1e5

思路：要想赢，就要走的点数别对方多，因为树上没有走回头路，所以一定要往最长链走才能赢，例如下图这幅图：

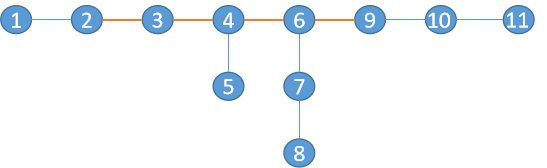
我们令A的起点是2，B的起点是9，连接他们的简单路我们称为“关键路径”，我们看先手的A，它可能到达的点只有1~8号点，1能走的所有链的长度d1为[1,1,3,5]（按从近到远排序），9能走的所有链的长度d2=[2,3,3,3]，同样按到9的距离排序，他当前的最优策略应该是看它左边的子树也就是无法被B干扰的点，如果在这棵子树中存在一条链，它的长度大于所有从9出发的链，那么A一定必胜，不需要考虑B怎么做，但在此图中不存在此情况，所以它要向更长的链也就是向右移动一格到3，接下来轮到B，B的策略也类似，但区别在于因为他是后手，所有只要存在这样一条链长度大于等于从2出发的所有链，就能必胜，此图也不存在此情况

来到下一轮，由于A、B位置改变，已经讨论过的走自子链就没有用了，更新新的图如下：

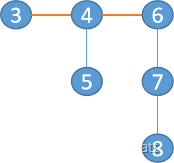
接下来和上一轮同理，A从3出发，优先走不会受B影响的点，也就是除了关键路径和已访问过的路径的其他路径，如果存在一条路径长度>从6出发的所有链的长度，那么他必胜，此图不符，轮到B，依然同理，发现6~8这条路长度为2，而从3出发的最长路3~5也是2，所以B有了必胜策略，游戏结束。我们按照此策略循环，看谁先找到最优策略，或者两个人汇合时，谁不能继续走。

所以知道了最优策略，我们现在要求关键路径，可以一个dfs实现，然后要求关键路径上的所有点到关键路径以外的所有链中最长链的长度，也可以一个dfs求出，对于一个关键路径上的点u,如果子节点v不在关键路径上，维护dis[u]=max(dis[u],dis[v]）即可。然后我们还要求从关键路径上每个点出发的所有链的长度，每移动一个节点，所有从起点出发的链的长度都要-1，但其实可以数学一下，我们求出两个起点出发所有链的长度d1,d2，然后假如A从起点移动了一格，到了编号为i1的点，那么再判断时我们只需要判断dis[i1]+1与从B的起点出发所有链的长度即可，省去了全部-1的操作，我们用st表求最大值即可

#include<bits/stdc++.h>
//#include<__msvc_all_public_headers.hpp>
using namespace std;
typedef long long ll;
const int N = 1e5 + 10;
int n;
int head[N];
struct Edge
{int v, next;
}e[N * 2];
int cnt = 0;
int path[N];
int s1, s2;
int d[N];
void addedge(int u, int v)
{e[++cnt].v = v;e[cnt].next = head[u];head[u] = cnt;
}//邻接链表存树
int rmqmax[N][18];
int rmqmax2[N][18];
void init(int n)
{//初始化for (int i = 0; i <= n; i++){d[i] = 0;head[i] = -1;rmqmax[i][0] = 0;rmqmax2[i][0] = 0;}cnt = 0;
}
void findpath(int u, int fa)
{//找到AB之间的简单路径for (int i = head[u]; ~i; i = e[i].next){int v = e[i].v;if (v == fa)continue;path[v] = u;if (v == s2){return;}findpath(v, u);}
}
map<int, bool>inp;
void dfs(int u, int fa)
{for (int i = head[u]; ~i; i = e[i].next){int v = e[i].v;if (v == fa)continue;dfs(v, u);if (inp.find(v) == inp.end())d[u] = max(d[u], d[v]);//对于不在关键路径上的子链，维护最大值}d[u] += 1;
}
void rmqinit(int n)
{for (int j = 1; (1 << j) <= n; j++){//j代表区间长度，以2的j次幂为单位for (int i = 1; i + (1 << j) - 1 <= n; i++){//i是区间起点，i+2的n次方减一是区间终点rmqmax[i][j] = max(rmqmax[i][j - 1], rmqmax[i + (1 << j - 1)][j - 1]);//求从i开始长2的j次方的区间的最大值和从i+2的j-1次方开始,长2的j次方的区间的最大值的最大值rmqmax2[i][j] = max(rmqmax2[i][j - 1], rmqmax2[i + (1 << j - 1)][j - 1]);}}
}
int rma(int l, int r)
{int k = log2l(r - l + 1);//求区间长度是2的几次幂return max(rmqmax[l][k], rmqmax[r - (1 << k) + 1][k]);//求左端点开始长k的区间的最大值，和从右端点减2的k次方+1的开始，长度为k的区间的最大值的最大值
}
int rma2(int l, int r)
{int k = log2l(r - l + 1);//求区间长度是2的几次幂return max(rmqmax2[l][k], rmqmax2[r - (1 << k) + 1][k]);//求左端点开始长k的区间的最大值，和从右端点减2的k次方+1的开始，长度为k的区间的最大值的最大值
}
int main()
{cin.tie(0);cout.tie(0);ios::sync_with_stdio(false);int t;cin >> t;while (t--){int n;cin >> n;inp.clear();init(n);cin >> s1 >> s2;for (int i = 1; i <= n - 1; i++){int u, v;cin >> u >> v;addedge(u, v);addedge(v, u);}findpath(s1, 0);vector<int>p;int now = s2;while (now != s1){inp[now] = 1;//标记在关键路径上的点p.push_back(now);//记录在关键路径上的点now = path[now];}inp[s1] = 1;p.push_back(s1);dfs(s1, 0);vector<int>dis;for (int i = 0; i < p.size(); i++){//记录关键路径上所有点的最长子链长度dis.push_back(d[p[i]] - 1);}int len = dis.size();vector<int>d1(len), d2(len);for (int i = 0; i < len - 1; i++){//从B的起点出发的所有链的长度d2[i] = dis[i] + i;}d2[len - 1] = dis[len - 1];for (int i = len - 1; i > 0; i--){//从A的起点触发的所有链的长度d1[len - i - 1] = dis[i] + len - i - 1;}d1[len - 1] = dis[0];for (int i = 0; i < len-1; i++){//st表维护链长的最大值rmqmax[i + 1][0] = d1[i];rmqmax2[i + 1][0] = d2[i];}rmqinit(len-1);int cnt1 = 0, cnt2 = 0;int it1 = 0, it2 = 0;bool ans = 1;while (1){int temp = rma2(1, len - it1 - 1);//从B的当前点出发的所有链的最大长度if (dis[len - it1 - 1] + cnt1 > temp){//从这个点出发的最长子链长度加上已经走过的步数ans = 1;break;}it1++;cnt1++;if (it1 + it2 == p.size()){//两个点汇合了，下一个人没法走了ans = 1;break;}temp = rma(1, len - it2 - 1);//从A的当前点出发的所有链的最大长度if (dis[it2] + cnt2 >= temp){ans = 0;break;}it2++;cnt2++;if (it1 + it2 == p.size()){ans = 0;break;}}cout << ans << endl;}return 0;
}
//100
//7
//2 3
//6 2
//2 5
//5 1 5 4
//4 3
//3 7
// 
//11
//2 9
//1 2
//2 3
//3 4
//4 5
//4 6
//6 7
//7 8
//6 9
//9 10
//10 11
//
//4
//1 2
//1 2
//3 1
//4 3
//
//4
//1 2
//1 2
//2 3
//3 4
//
//4
//1 4
//1 2 2 3 3 4
//
//5
//1 2
//1 2
//1 3
//3 4
//2 5