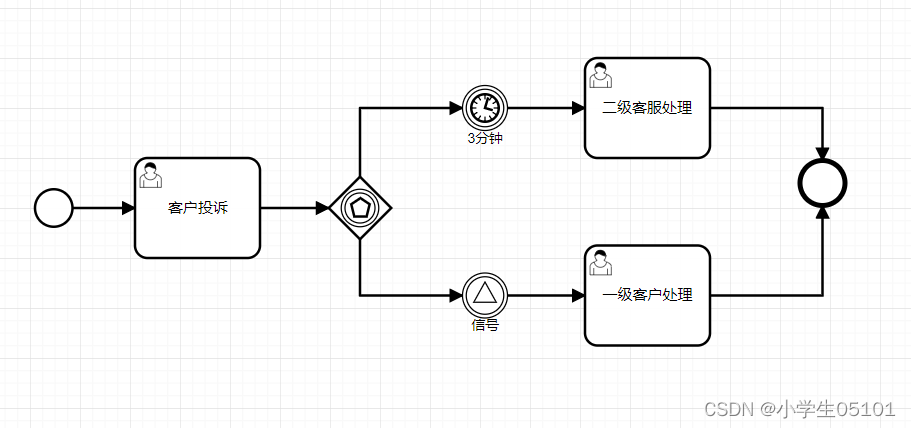
什么是图
图是一个由点的集合和边的集合所构成的数据结构。
图分为有向图和无向图。其中无向图也可以理解为有向图,所以可以认为所有的图都是有向图。
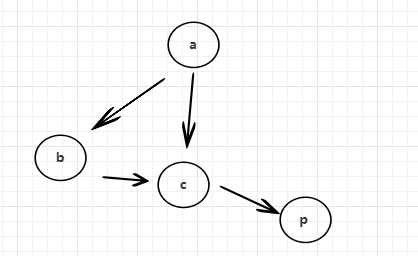
比方说,有这么一张图。其中a指向bc,b指向c,c指向p。边是带方向的,所以这是一个有向图。
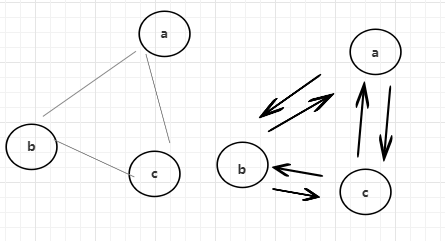
而无向图呢? a连b,b连c,c连a。完全可以理解为ab互相指向,bc互相指向,ca互相指向,所以无向图也可以理解为都是有向图。
而图的表达方式有很多,其中常见的有邻接表法,邻接矩阵法等等。图的算法不难,难的是图的数据结构的表达。
比如说,给定一个n * 3的二维数组,[1 , 3 , 5],[0 , 5 , 5 ],[2 , 6 , 5]其中[i][0]代表的是边的权重,[i][1],[i][2]代表的是边从哪到哪。给的是每条边的权重以及从哪到哪,根据每条边画出来的图是这样的。这也是一种图的表示。
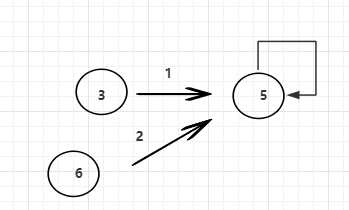
甚至更可以用1维数组表示一张图,所以用不同的方式表达图,所用到的解法也不同,每一种coding都要练习,那是不是可以将结构进行统一?无论什么样的图,都转换成自己的结构,将抽象化的图通过代码变得具象化,面向对象编程的思想更多一些。
代码
通过代码将点进行转化,Node对象中封装了这个点的所有基本信息,点的值,连接到这个点上的边有多少,从这个点出去的边有多少。
/*
* 点的描述
* */
public class Node {//点本身valuepublic int value;//入度(有多少个点的边直接指向该点)public int in;//出度(从自己出发,直接指向别人的)public int out;//从自己出发能找到的边public ArrayList<Edge> edges;//从自己出发能找到的点public ArrayList<Node> nexts;public Node(int val){this.value = val;this.in = 0;this.out = 0;edges = new ArrayList<>();nexts = new ArrayList<>();}
}
边的描述信息,包含边的权重,从哪个点连接到哪个点。
/*
* 边的描述信息
* */
public class Edge {//边的权重public int weight;//从哪个点出来public Node from;//连接到哪个点public Node to;public Edge(int weight,Node from,Node to){this.weight = weight;this.from = from;this.to = to;}
}
一个图是由多个点和边所组成,所以包含了所有的点信息和边的信息,其中HashMap是具体的点的值和封装的点的对象。
/*
* 图的描述,包含了所有的点和所有的边
* */
public class Graph {public HashMap<Integer,Node> nodes;public HashSet<Edge> edges;public Graph(){nodes = new HashMap<>();edges = new HashSet<>();}
}
生成图代码
以图形式为二维数组为例,[i][0]位置是边的权重,[i][1],[i][2]是从哪个点连到哪个点。
public class GraphGenerator {public static Graph createGraph(int[][] matrix) {Graph graph = new Graph();for (int i = 0; i < matrix.length; i++) {int weight = matrix[i][0];int from = matrix[i][1];int to = matrix[i][2];if (!graph.nodes.containsKey(from)){graph.nodes.put(from,new Node(from));}if (!graph.nodes.containsKey(to)){graph.nodes.put(to,new Node(to));}Node fromNode = graph.nodes.get(from);Node toNode = graph.nodes.get(to);Edge edge = new Edge(weight,fromNode,toNode);fromNode.nexts.add(toNode);fromNode.out++;toNode.in++;fromNode.edges.add(edge);graph.edges.add(edge);}return graph;}
}