💥💥💞💞欢迎来到本博客❤️❤️💥💥
🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。
⛳️座右铭:行百里者,半于九十。
📋📋📋本文目录如下:🎁🎁🎁
目录
💥1 概述
📚2 运行结果
🎉3 参考文献
🌈4 Matlab代码实现
💥1 概述
拆分布雷格曼方法(Split Bregman Method)是一种用于全变分去噪的迭代算法。它通过最小化经过全变差正则化的优化问题来实现去噪。以下是实施拆分布雷格曼方法进行全变差去噪的步骤如下:
1. 数据准备:将待去噪的图像表示为二维矩阵或张量形式。如果图像是彩色的,可以将其转换为灰度图像。
2. 定义目标函数:构建优化问题目标函数,将待去噪的图像的全变差作为正则化项。目标函数的形式可能因具体问题而异,但一般形式为最小化损失函数(例如均方差损失)和全变差正则化项之和。
3. 拆分变量:将图像分解为两个变量,通常记为u和v,其中u是去噪后的图像,v是对图像梯度的估计。
4. 迭代求解:使用拆分布雷格曼方法迭代求解优化问题。具体步骤如下:
a. 固定u,更新v:在保持u不变的情况下,根据当前v的值,通过解决子问题来更新v。这通常涉及到用梯度算子计算图像梯度,并应用软阈值来减少噪声。
b. 固定v,更新u:在保持v不变的情况下,根据当前u和v的值,通过解决子问题来更新u。这通常涉及到通过最小化目标函数来求解图像u的最优解。
c. 更新v:更新v的值,将其设置为当前图像u的梯度。
d. 迭代以上步骤,直到达到收敛条件。
5. 返回结果:在迭代收敛后,得到的最终图像u即为去噪后的结果。
通过拆分布雷格曼方法,可以实现全变差去噪,并获得去噪后的图像。该方法在图像处理和计算机视觉领域得到广泛应用,尤其对于去除噪声并保持图像细节的有效性很好。请注意,具体的算法细节和参数选择可能因具体问题而有所不同。
📚2 运行结果
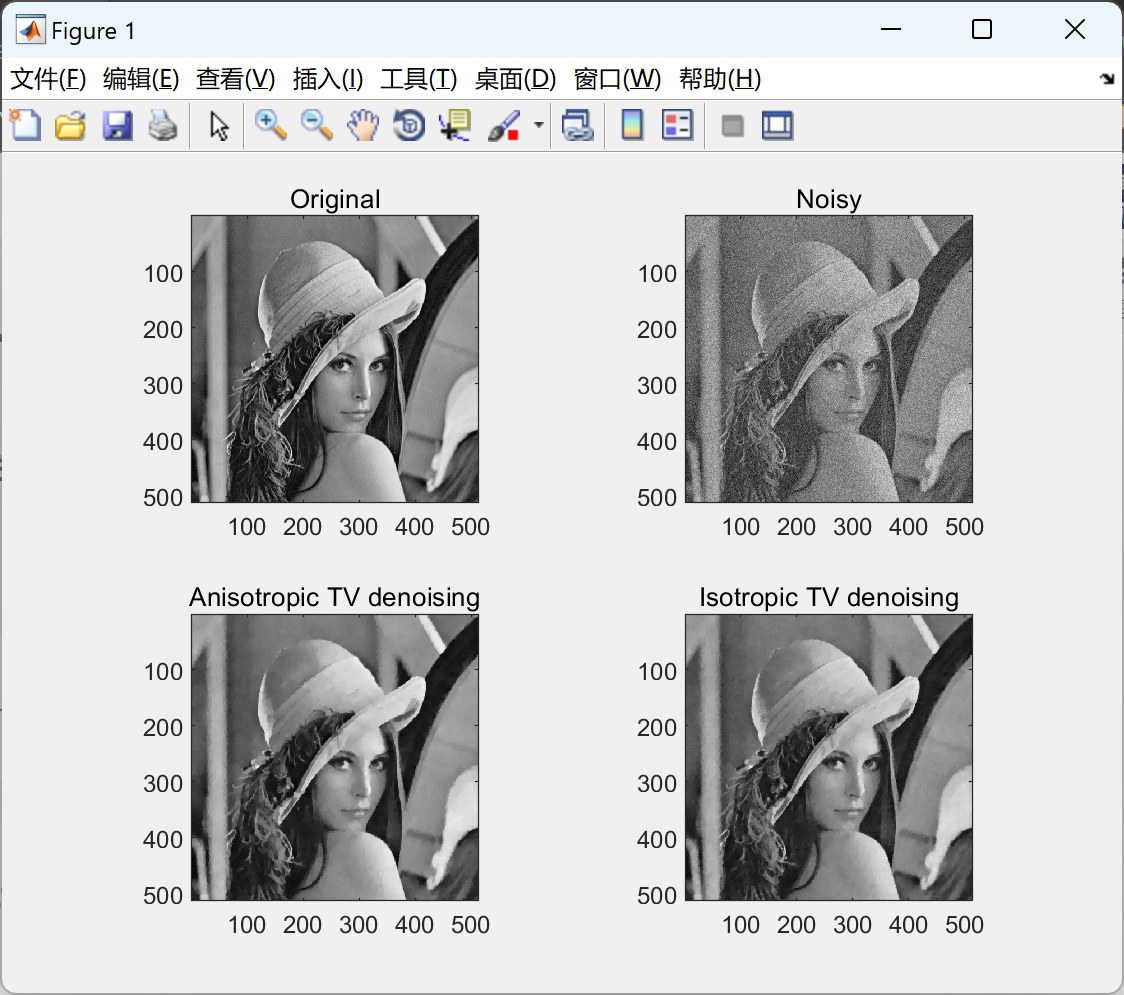
部分代码:
function u = SB_ATV(g,mu)
% Split Bregman Anisotropic Total Variation Denoising
%
% u = arg min_u 1/2||u-g||_2^2 + mu*ATV(u)
%
% g : noisy image
% mu: regularisation parameter
% u : denoised image
%
g = g(:);
n = length(g);
[B Bt BtB] = DiffOper(sqrt(n));
b = zeros(2*n,1);
d = b;
u = g;
err = 1;k = 1;
tol = 1e-3;
lambda = 1;
while err > tol
fprintf('it. %g ',k);
up = u;
[u,~] = cgs(speye(n)+BtB, g-lambda*Bt*(b-d),1e-5,100);
Bub = B*u+b;
d = max(abs(Bub)-mu/lambda,0).*sign(Bub);
b = Bub-d;
err = norm(up-u)/norm(u);
fprintf('err=%g \n',err);
k = k+1;
end
fprintf('Stopped because norm(up-u)/norm(u) <= tol=%.1e\n',tol);
end
function [B Bt BtB] = DiffOper(N)
D = spdiags([-ones(N,1) ones(N,1)], [0 1], N,N+1);
D(:,1) = [];
D(1,1) = 0;
B = [ kron(speye(N),D) ; kron(D,speye(N)) ];
Bt = B';
BtB = Bt*B;
end
🎉3 参考文献
部分理论来源于网络,如有侵权请联系删除。
[1]Goldstein and Osher, The split Bregman method for L1 regularized problems
SIAM Journal on Imaging Sciences 2(2) 2009
[2]Micchelli et al, Proximity algorithms for image models: denoising
Inverse Problems 27(4) 2011
[3]李潇瑶,王炼红,周怡聪等.自适应非局部3维全变分彩色图像去噪[J].中国图象图形学报,2022,27(12):3450-3460.
[4]赵鑫春,李碧原,张军.一种改进全变分的图像去噪算法模型[J].计算机辅助工程,2022,31(03):42-48+54.DOI:10.13340/j.cae.2022.03.008.