插值法

作用

数模比赛中，常常需要根据已知的函数点进行数据、模型的处理和分析，但可能出现数据极少或者数据缺失的情况，此时数据并不能支撑分析，这时候就需要用到一些数学的方法，去模拟产生一些新的但又比较靠谱的值来满足数据的需求。以上提到正是插值法的作用

定义

设函数y=f(x)在区间[a,b]上有定义，且已知在点
$$a<=x_0<x_1<...<x_n<=b$$
上的值分别为：
$$y_0,y_1,...<y_n$$
若存在一简单函数P(x)，使得
$$P(x_i)=y_i(i=0,1,2,...,n)$$
则称P(x)为f(x)的插值函数，点x₀,x₁,…,x_n称为插值节点，包括插值节点的区间[a,b]称为插值区间，求插值函数P(x)的方法称为插值法。

概念

常用的三种插值法的概念

1. 插值多项式。若P(x)是次数不超过n的代数多项式，即

$$P(x)=a_0+a_{1}x+...+a_n{x}^n,$$

2. 若P(x)为分断多项式，就称分段插值
3. 若P(x)为三角多项式，就称三角插值

本文只介绍多项式插值和分段插值。

一维插值问题

• 已知一些数据x_i，y_i，这些数据能够模拟出一个f(x)函数（图像）。通过将新的数据x^* 带入f(x)函数中求得y^*。

一维插值多项式原理

定理

• 已知矩阵X和矩阵Y都是可逆矩阵，那么AX=Y可以化成A=YX^-。那么若矩阵A的行列式不为0，则方程组有唯一解
• 行列式可以用范德蒙德行列式法计算
• 若方程组有唯一解，那么多项式确定唯一存在

拉格朗日插值法和牛顿插值法

红色是目标函数，蓝色是通过拉格朗日插值法模拟出来的函数图像。可以看到在次数增多时，两端图像产生明显的震荡。

• 多项式插值中常用的有拉格朗日插值法。但该方法在高次插值时会出现两端波动极大，产生明显的震荡，即产生龙格现象。因此不熟悉曲线运动趋势的前提下，不要轻易使用高次插值。加上函数难以使用，因此在数模比赛里多项式插值也很少使用

• 牛顿插值法每次只需要在前n项的基础上，即原来的函数上添加新的项就能产生新的函数，与拉格朗日插值法相比，牛顿插值法计算过程具有继承性。
• 但牛顿插值法也存在龙格现象问题。

总结一下：

• 插值多项式次数越高，精度未必显著提高
• 插值多项式次数越高，摄入误差可能显著增大
• 实际上不仅要求插值函数与被插值函数在所有节点处有相同的函数值，它也需要在一个或全部节点上插值多项式与被插函数有相同的低阶甚至高阶的导数值。因此这种插值多项式并不能全面反映被插值函数的性态

基于插值多项式的缺点，在数模比赛中通常会使用分段插值法

埃尔米特插值

• 直接使用Hermite插值得到的多项式次数较高，也存在龙格现象，因此实际应用重往往使用分段三次Hermite插值多项式（PCHIP)

分段线性插值

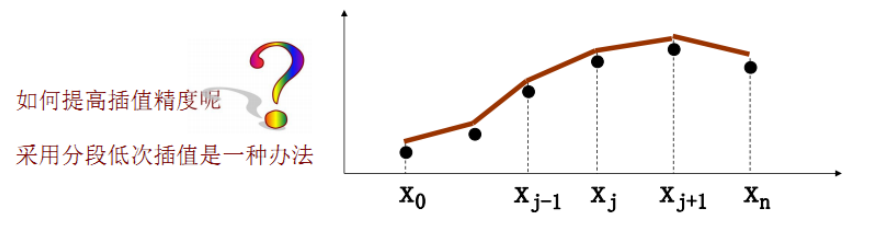
若新插入的值x_i位于x_j-1到x_j之间，那么只需要模拟出x_j-1到x_j之间的插值函数即可。

分段三次埃尔米特插值法代码

Matlab有内置的函数，其实现过程已经帮我们封装好了，会调用就行了

函数原型

p=pchip(x,new_x)

x是已知的样本点的横坐标；y是已知的样本点的纵坐标；new_x是要插入对应的点的横坐标，通过pchip函数模拟出new_x对应的纵坐标

假设x的范围是[-pi,pi]；y=sin(x)；new_x=-pi:0.1:pi（从-pi到pi间隔0.1一个横坐标）

那么可以这样调用

x=-pi:pi;
y=sin(x);
new_x=-pi:0.1:pi;
p=pchip(x,y,new_x);%%p是通过Hermite插值法模拟出来的对应new_x的纵坐标
plot(x,y,'o',new_x,p,'r-');
legend('样本点','三次埃尔米特插值','Location','southeast');

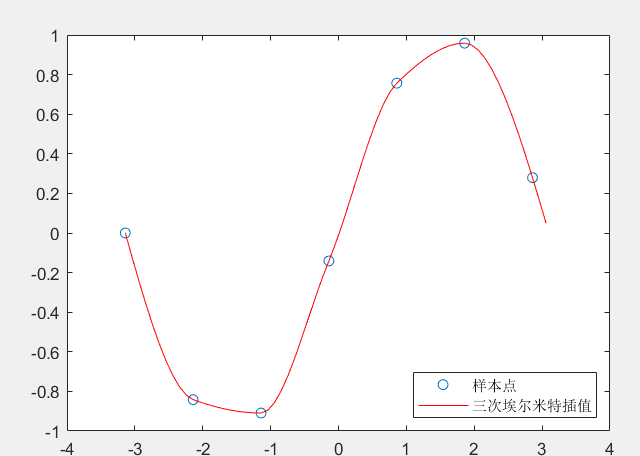
可以看到样本点函数对应的是o点图，而埃尔米特插值法模拟出来的函数图像是红色-线

三次样条插值及其代码

• 三次样条插值的matlab内置函数是

  p = spline (x,y, new_x)
  

• x是已知的样本点的横坐标;y是已知的样本点的纵坐标;new_x是要插入处对应的横坐标

同样的用三次样条插值法模拟出来new_x对应的图像

x=-pi:pi;
y=sin(x);
new_x=-pi:0.1:pi;
p1=pchip(x,y,new_x);%%p是通过Hermite插值法模拟出来的对应new_x的纵坐标
p2=spline(x,y,new_x);
plot(x,y,'r-',new_x,p1,'b.',new_x,p2,'g*');legend('样本点','三次埃尔米特插值','三次样条插值','Location','southeast');

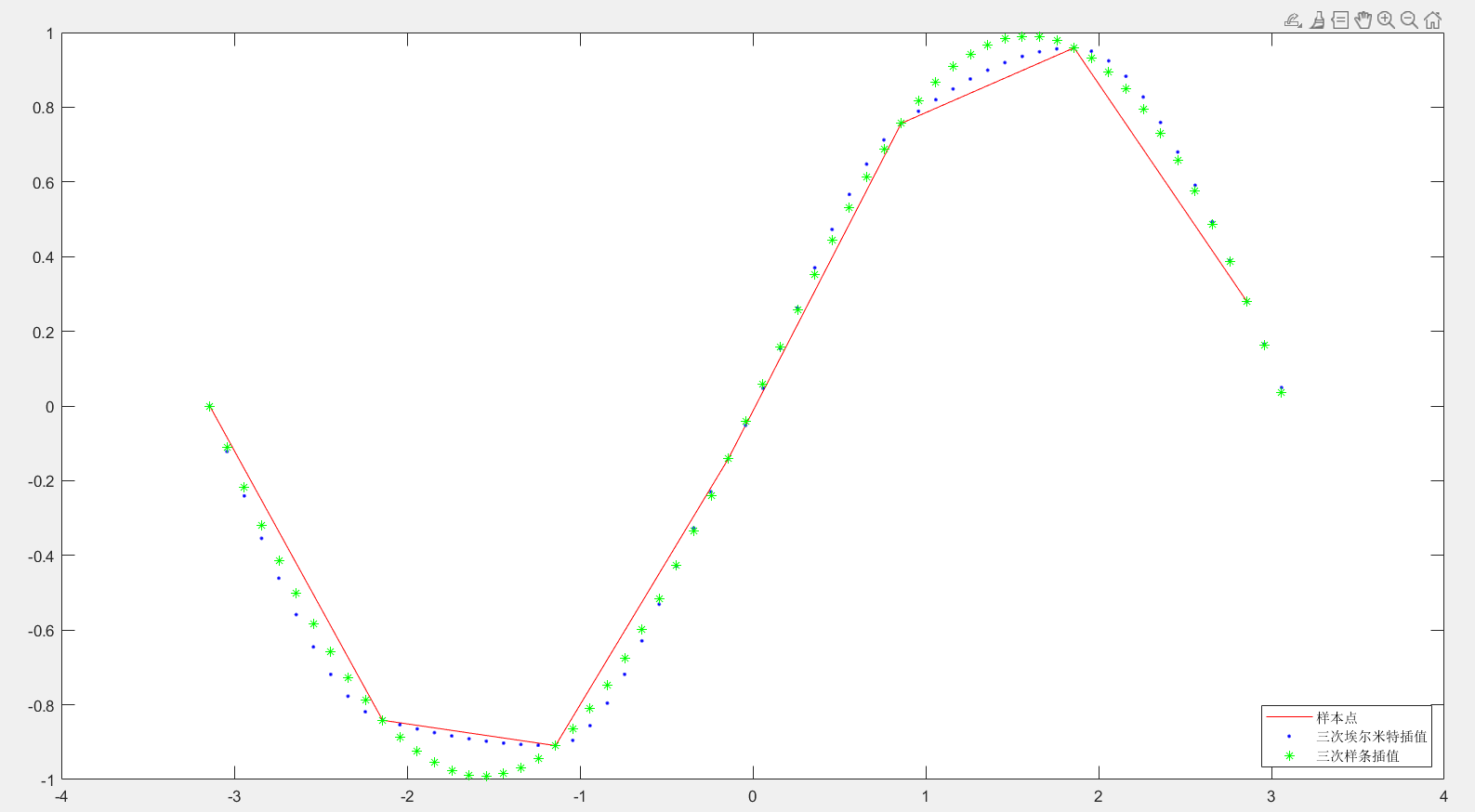
可以看出，三次样条生成的曲线更加光滑。在实际建模中， 由于我们不知道数据的生成过程，因此这两种插值都可以使用

例子

先有2009到2018的中国人口数，通过三次埃尔米特插值预测或三次样条插值预测预测出2019到2023的中国人口数

year=2009:2018;
population=[133126,133770,134413,135069,135738,136427,137122,137866,138639, 139538];
p1=pchip(year,population,2019:2023);
p2=spline(year,population,2019:2023);
plot(year,population,'r-',2019:2023,p1,'b.',2019:2023,p2,'g*');
legend('样本点','三次埃尔米特插值预测','三次样条插值预测','Location','SouthEast')

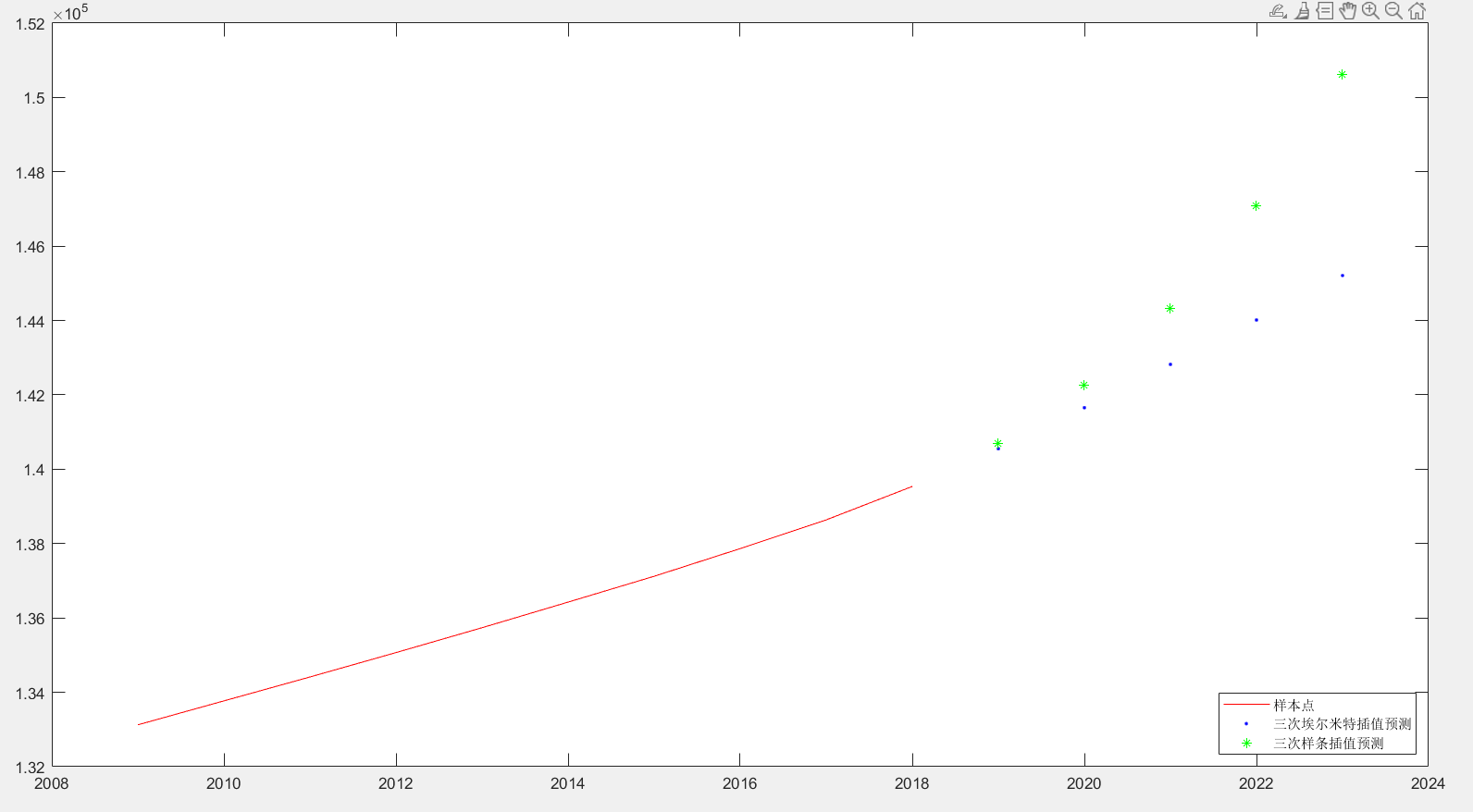
另外若需要作出两张图形，需要在作图前标明是第几张图，否则系统判定是只在 figure(1)上作图，后来的图像会将前面的图像刷新掉

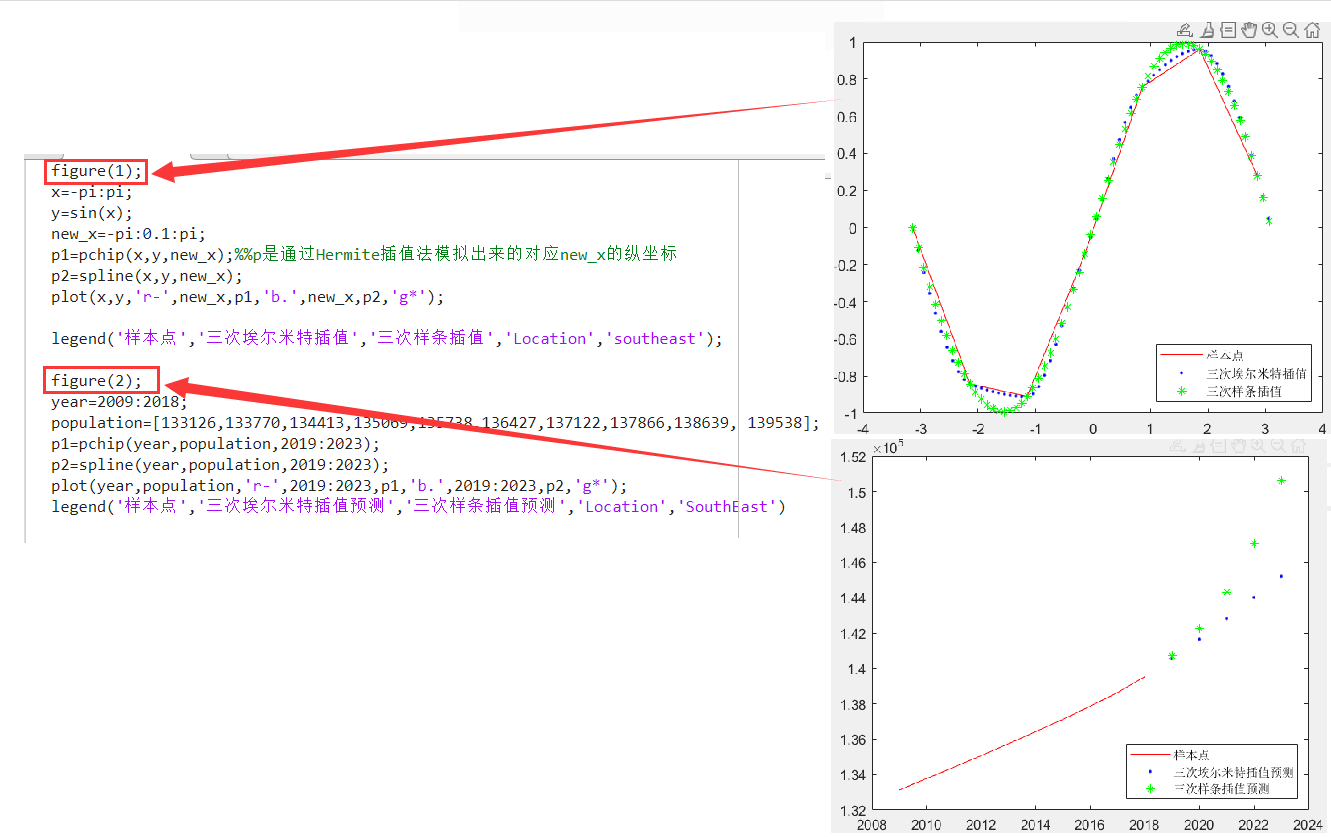
n维数据的插值（了解）

函数原型

p=interpn(x1,x2,...,xn,y,new_x1,new_x2,...,new_xn,method)

• x1,x2,…,xn是已知的样本点的横坐标
• y是已知的样本点的纵坐标
• new_x1,new_x2,…,new_xn是要插入点的横坐标
• method是要插值的方法
• • ‘spline’：三次样条插值法；(最为精准)
  • ‘pchip’：三次埃尔米特插值法
  • ‘linear’:线性插值（默认算法）
  • ‘cubic’:三次插值
  • ‘nearest’：最邻近插值算法

x=-pi:pi;
y=sin(x);
new_x=-pi:0.1:pi;
p2=spline(x,y,new_x);

等价于

x=-pi:pi;
y=sin(x);
new_x=-pi:0.1:pi;
p2=interpn(x,y,new_x,'spline');

• ‘nearest’：最邻近插值算法

x=-pi:pi;
y=sin(x);
new_x=-pi:0.1:pi;
p2=spline(x,y,new_x);

等价于

x=-pi:pi;
y=sin(x);
new_x=-pi:0.1:pi;
p2=interpn(x,y,new_x,'spline');