2023.8.9
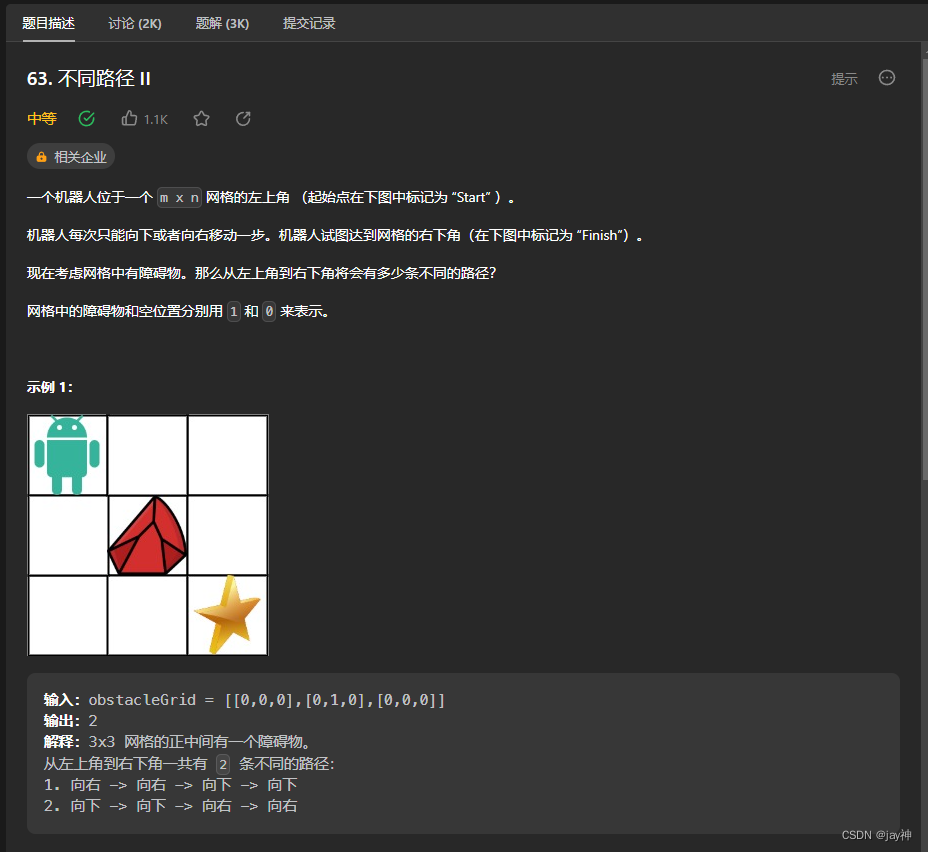 这题是不同路径I的升级版,在路径上增加了障碍物,有障碍物的地方无法通过。
这题是不同路径I的升级版,在路径上增加了障碍物,有障碍物的地方无法通过。
我的思路依然还是使用动态规划,dp[i][j]的含义依然是到(i,j)这个位置的路径个数。只需要在dp数组中将有障碍物的地方赋为0。大致步骤如下:
- 先进行极端情况判断:当起始位置为障碍物时,无法到达终点,直接返回0。
- 然后对第一行和第一列进行初始化,有障碍物的地方赋为0,无障碍物的地方赋为其左方或者上方的值。
- 用两个for循环递推赋值,递推公式和不同路径I 一样,当前位置的路径个数 = 上方位置路径个数 + 左方位置的路径个数。
代码如下:
class Solution {
public:int uniquePathsWithObstacles(vector<vector<int>>& obstacleGrid) {if(obstacleGrid[0][0] == 1) return 0; //起点就是障碍物int m = obstacleGrid.size();int n = obstacleGrid[0].size();vector<vector<int>> dp(m , vector<int>(n));dp[0][0] = 1;//第一行初始化赋值for(int i=1; i<n; i++){//有障碍物if(obstacleGrid[0][i] == 1) dp[0][i] = 0;//无障碍物else dp[0][i] = dp[0][i-1];}//第一列初始化赋值for(int i=1; i<m; i++){if(obstacleGrid[i][0] == 1) dp[i][0] = 0;else dp[i][0] = dp[i-1][0];}//遍历递推赋值for(int i=1; i<m; i++){for(int j=1; j<n; j++){if(obstacleGrid[i][j] == 1) dp[i][j] = 0; //有障碍物就不用赋值了else dp[i][j] = dp[i-1][j] + dp[i][j-1]; }}return dp[m-1][n-1];}
};




![[分享]STM32G070 串口 乱码 解决方法](https://img-blog.csdnimg.cn/f9be8803e97e4d43b753460e44f9315f.png)