💥💥💞💞欢迎来到本博客❤️❤️💥💥
🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。
⛳️座右铭:行百里者,半于九十。
📋📋📋本文目录如下:🎁🎁🎁
目录
💥1 概述
📚2 运行结果
🎉3 参考文献
🌈4 Matlab代码实现
💥1 概述
本文实现了一个参数非线性估计器,该估计器推广了几种小波收缩去噪方法。它致力于加性高斯噪声,采用多元统计方法考虑不同小波子带之间存在的空间和分量间相关性,使用斯坦无偏风险估计器(SURE)原理推导出最佳参数。小波选择是一个稍微冗余的多波段几何双小波框架。多光谱遥感影像实验优于传统的小波去噪技术(包括曲线)。
基于定向M波段双树(希尔伯特)小波对多分量/彩色图像进行降噪是一种高级的图像去噪方法。它结合了多分量图像处理和小波变换,并利用定向M波段双树小波的特性来保留图像的纹理细节和边缘信息,同时抑制图像中的噪声。
基于定向M波段双树(希尔伯特)小波的图像去噪过程按照以下步骤进行:
1. 分解图像:
将多分量/彩色图像分解为不同频带的小波系数。这里采用定向M波段双树小波,可以在不同尺度和方向上捕捉图像的特征。
2. 降噪处理:
对每个小波频带的系数进行降噪处理。采用适当的阈值方法对小波系数进行阈值处理,将噪声系数置零或进行柔和的修正,以保留有用的图像信息。
3. 重构图像:
对降噪后的小波系数进行逆变换,将其合并重构为降噪后的图像。利用双树结构和希尔伯特变换,可以确保重构图像具有较好的平滑性和细节保留性。
4. 结果评估:
对降噪后的图像进行质量评估,比较与原始图像的差异,常用的评估指标包括峰值信噪比(PSNR)、结构相似性指标(SSIM)等。
通过基于定向M波段双树(希尔伯特)小波的图像降噪方法,可以在去除图像噪声的同时,保持图像的细节和纹理信息,提高图像质量。然而,方法的实施过程相对复杂,需要对小波变换的理论和算法有较深的理解,并根据具体问题选择合适的参数和阈值方法。因此,在实际应用中需要进行实验和调整,以获得最佳的去噪效果。
📚2 运行结果

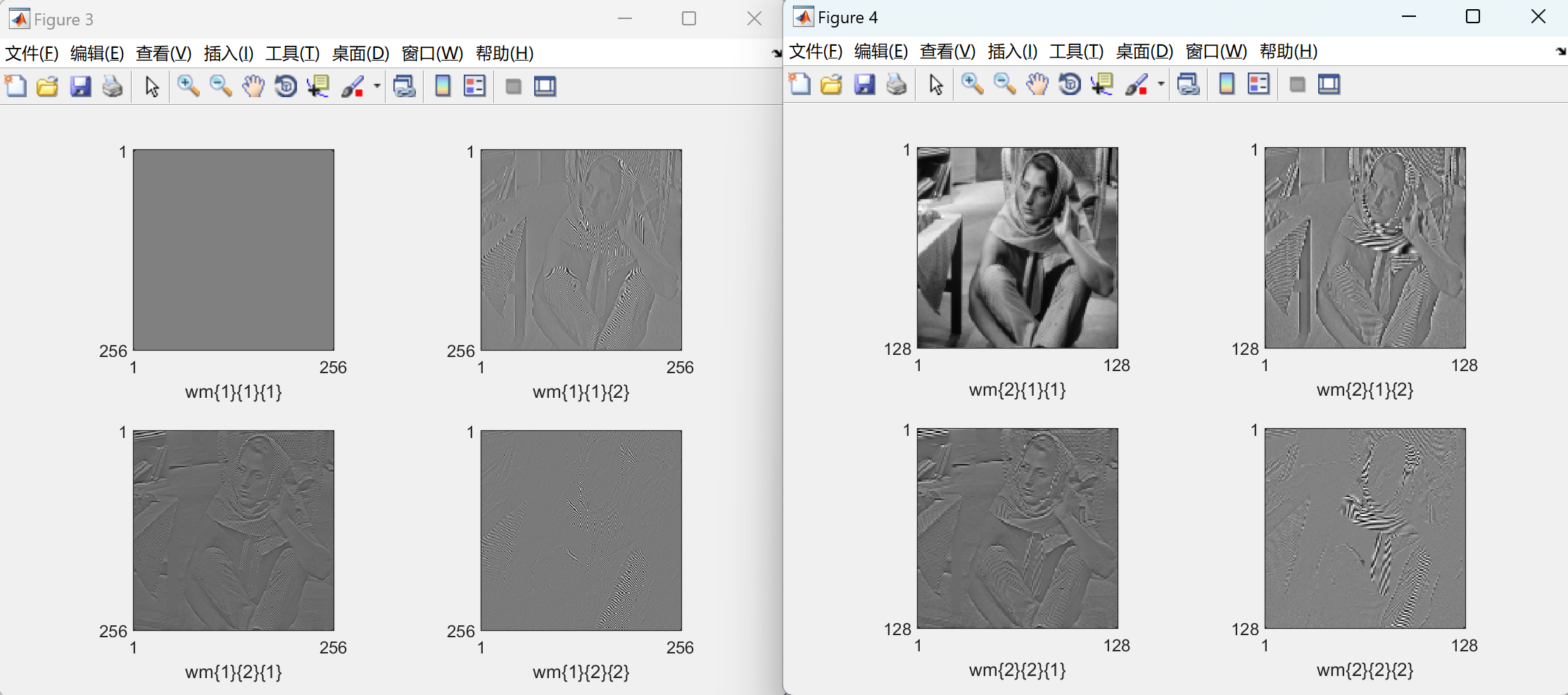
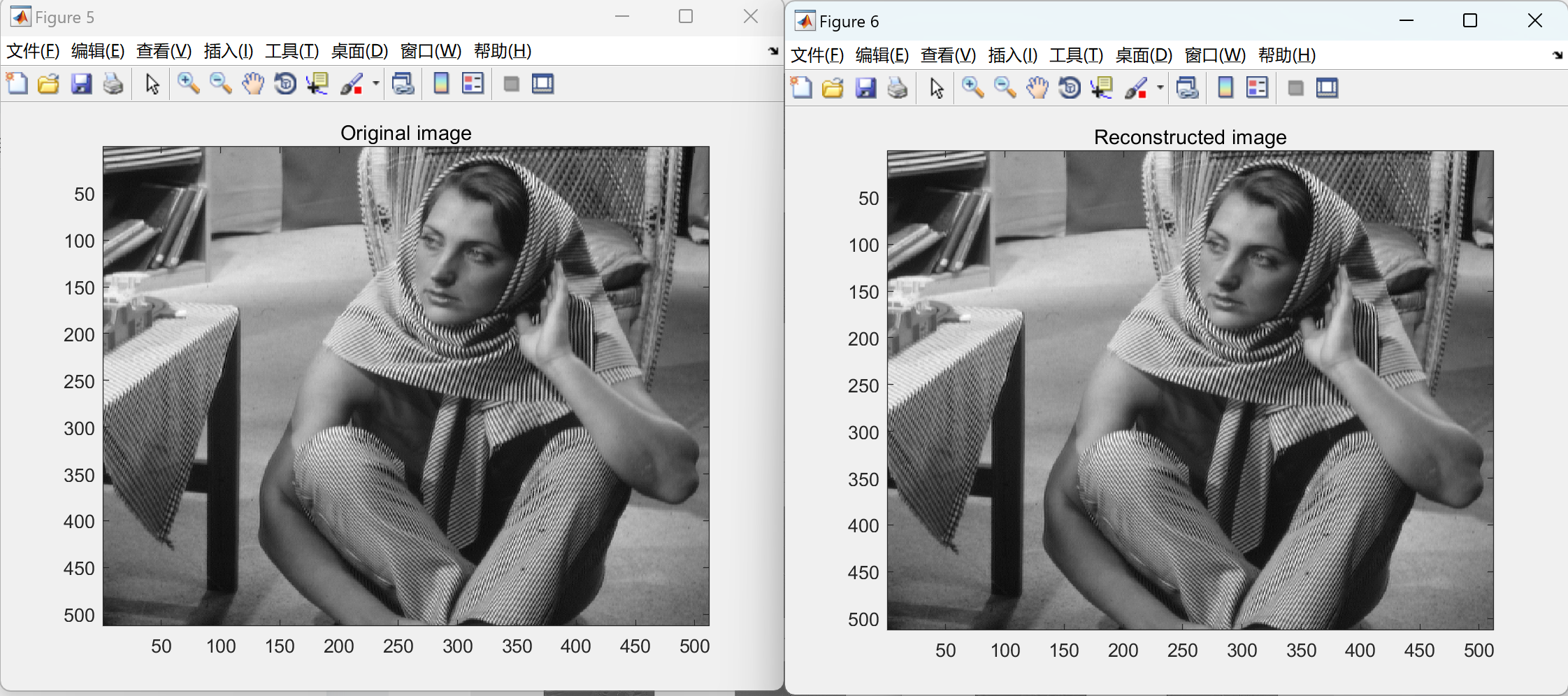
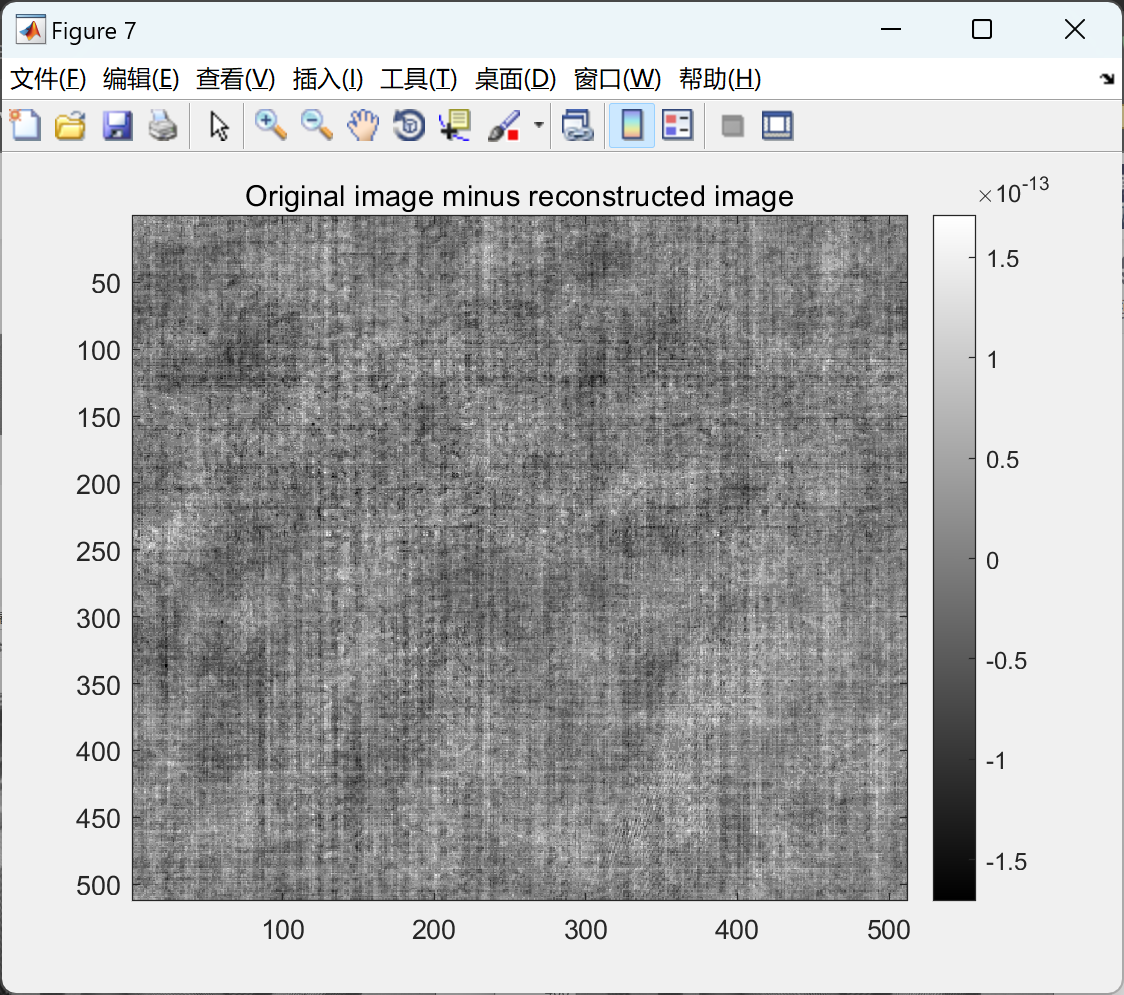
部分代码:
%decomposition
[wp,wm,H1,H2,HH1,HH2,G,Gh]=dualtreeM2D_freq(x,m,rm);
%plots of the coefficients
plot_dualtree_Mband2D(wp)
plot_dualtree_Mband2D(wm)
%reconstruction
xrec = idualtreeM2D_freq(wp,wm,rm,H1,H2,HH1,HH2,G,Gh);
disp('Original image norm:');
norm(x,'fro').^2
disp('Reconstructed image norm:');
norm(xrec,'fro').^2
disp('Norm of the difference between the original image and the reconstructed one:');
norm(x-xrec,'fro').^2
figure
imagesc(x)
title('Original image')
colormap(gray(256))
figure
imagesc(xrec)
title('Reconstructed image')
colormap(gray(256))
figure
imagesc(x-xrec)
title('Original image minus reconstructed image')
colormap(gray(256))
colorbar
🎉3 参考文献
部分理论来源于网络,如有侵权请联系删除。
* several dual-tree M-band wavelet transforms from: Image analysis using a dual-tree M-band wavelet transform, IEEE TRANSACTIONS ON IMAGE PROCESSING, 2006, Image analysis using a dual-tree M-band wavelet transform | IEEE Journals & Magazine | IEEE Xplore
* a neighborhood choice from: Noise covariance properties in dual-tree wavelet decompositions, IEEE TRANSACTIONS ON INFORMATION THEORY, 2007, Noise Covariance Properties in Dual-Tree Wavelet Decompositions | IEEE Journals & Magazine | IEEE Xplore
* the non-linear Stein estimator: A nonlinear Stein-based estimator for multichannel image denoising, IEEE TRANSACTIONS ON SIGNAL PROCESSING, 2008, A Nonlinear Stein-Based Estimator for Multichannel Image Denoising | IEEE Journals & Magazine | IEEE Xplore
* relative merits of different directional 2D wavelets are detailed in: A Panorama on Multiscale Geometric Representations, Intertwining Spatial, Directional and Frequency Selectivity, SIGNAL PROCESSING, 2011, Redirecting