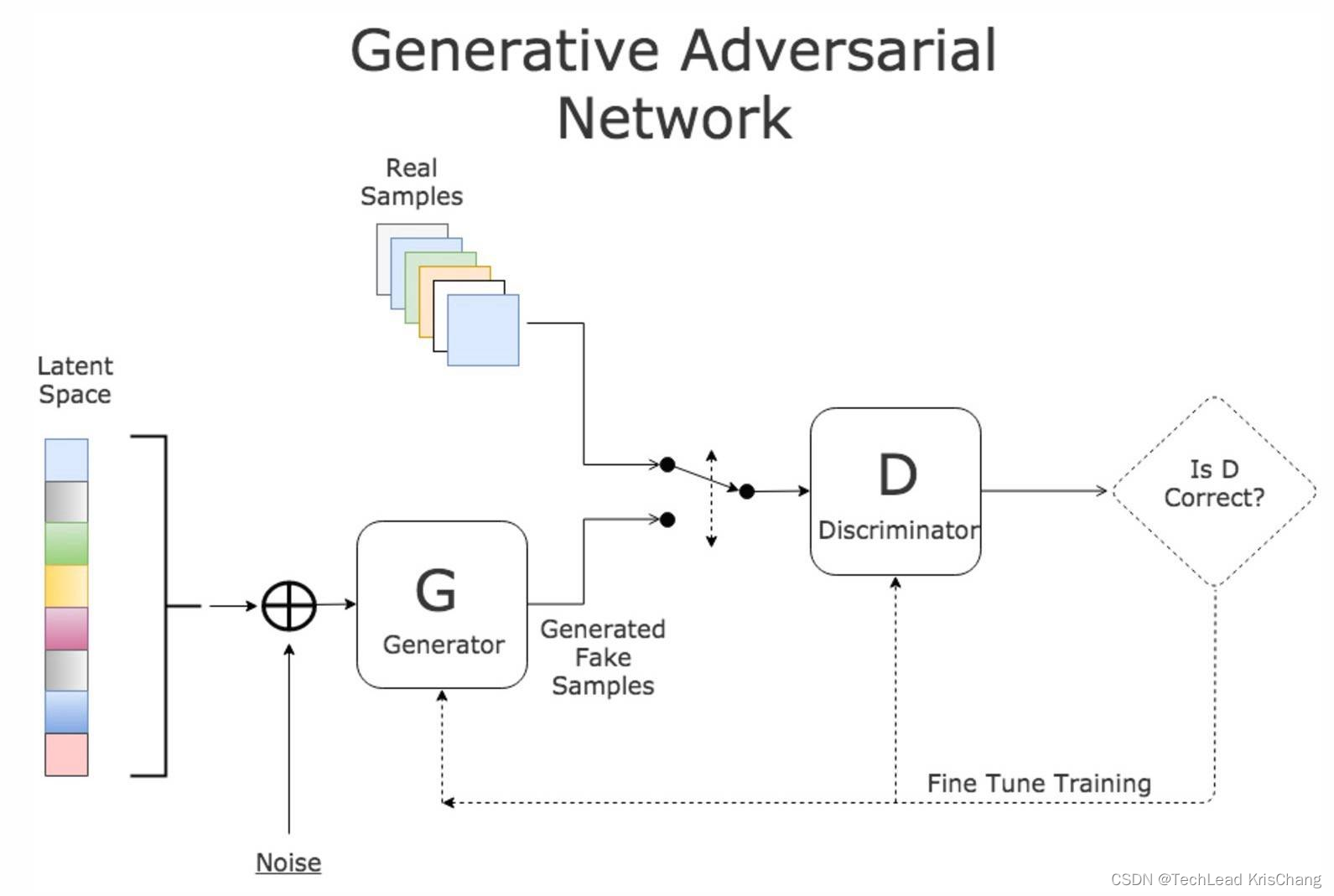
这里结合大模型的学习,主要分析Layer Norm、RMS Norm和Deep Norm的异同,与此同时,究竟是在之前执行Normalization(Pre-Norm)还是之后执行(Post-Norm),也是一个比较喜欢拿来讨论的知识点。
一、为什么要做Normalization?
ICS问题出现的根本原因在于神经网络每层之间,无法满足基本假设"独立同分布"。深度神经网络涉及到很多层的叠加,而每一层的参数更新会导致上层的输入数据分布发生变化,通过层层叠加,高层的输入分布变化会非常剧烈,这就使得高层需要不断去重新适应底层的参数更新。为了训好模型,我们需要非常谨慎地去设定学习率、初始化权重、以及尽可能细致的参数更新策略。
ICS( Internal Covariate Shift)问题导致的后果:
- 上层参数需要不断适应新的输入数据分布,降低学习速度;
- 下层输入的变化可能趋向于变大或者变小,导致上层落入饱和区,使得学习过早停止;
- 每层的更新都会影响到其它层,因此每层的参数更新策略需要尽可能的谨慎;
二、Pre or Post?
Transformer的block模块里面包含了多处Normalization,具体结构如下:
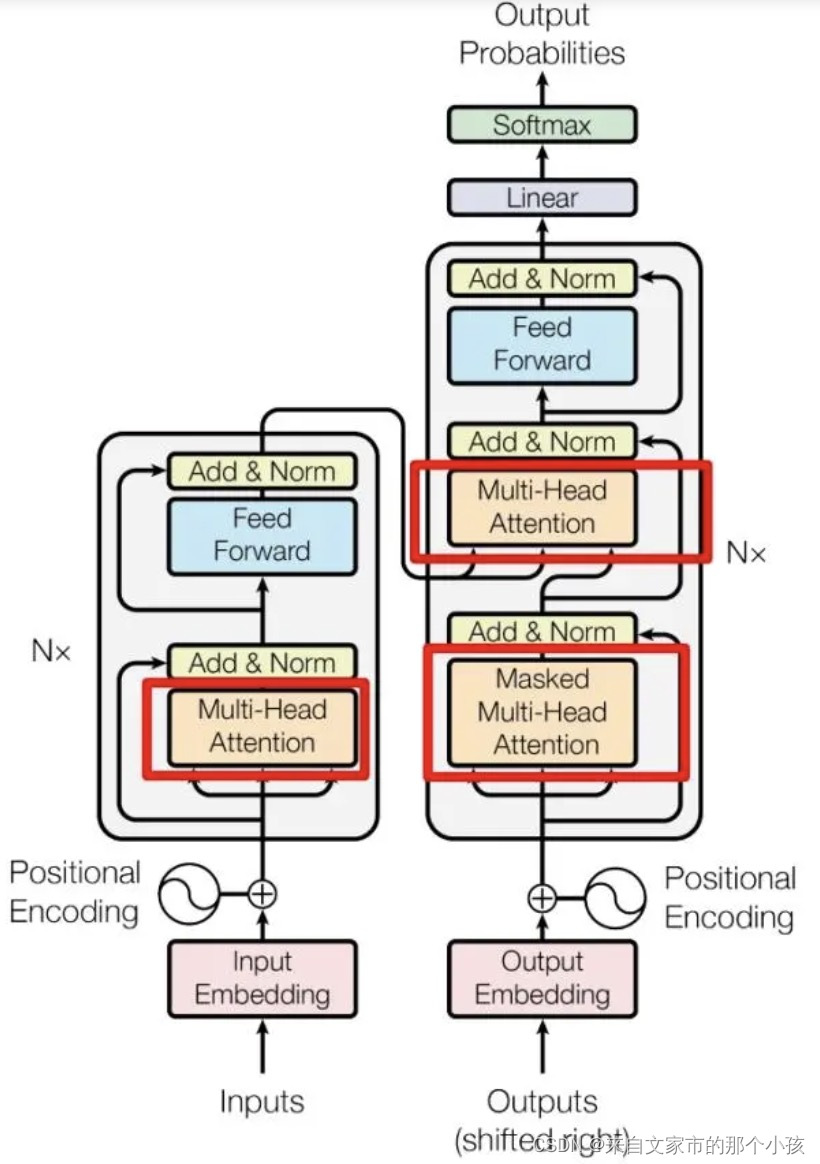
从图中可以看出,经过多头(multi-head)的self-attention之后结合残差网络,再做一次归一化。简化一下,如下图所示,

Pre-Norm的公式为:
Post-Norm的公式为:
问题一、为什么Pre Norm的效果不如Post Norm?Pre Norm的深度有“水分”!也就是说,一个L层的Pre Norm模型,其实际等效层数不如L层的Post Norm模型,而层数少了导致效果变差了?
原因:
所以在Pre Norm中多层叠加的结果更多是增加宽度而不是深度,层数越多,这个层就越“虚”。说白了,Pre Norm结构无形地增加了模型的宽度而降低了模型的深度,而我们知道深度通常比宽度更重要,所以是无形之中的降低深度导致最终效果变差了!
post-norm和pre-norm其实各有优势,post-norm在残差之后做归一化,对参数正则化的效果更强,进而模型的鲁棒性也会更好;pre-norm相对于post-norm,因为有一部分参数直接加在了后面,不需要对这部分参数进行正则化,正好可以防止模型的梯度爆炸或者梯度消失,因此,这里笔者可以得出的一个结论是如果层数少post-norm的效果其实要好一些,如果要把层数加大,为了保证模型的训练,pre-norm显然更好一些。
问题二:为什么Layer Normalization要加在F的前面,而不是F的后面呢?
因为做完Layer Normalization之后的数据不能和平常的数据加在一起,如果这样做的话残差中从上一层出来的信息会占很大比重,这显然并不合理。
三、BatchNorm or LayerNorm?
这个问题争论了很久,也是面试官比较喜欢问的一个问题,貌似有点不死不休的意思。到底哪个好一定是有个定论吗?还是说不同场景下的选择?抑或是仅是理论上的讨论,在实操上并没有明显的性能差异?
首先列举一些网络中的解释:
1. BatchNorm适用于CV,而LayerNorm适用于NLP,这是由两个任务的本质差异决定的,视觉的特征是客观存在的特征,而语义特征更多是由上下文语义决定的一种统计特征,因此他们的标准化方法也会有所不同。
2. layernorm更容易并行训练。当每个device用不同的minbatch训练,我们需要额外地同步各个device上的batchnorm,用layernorm则不需要。
3. layernorm所带来的hidden layer分布上的稳定性,促进了更平滑的梯度,更快的训练速度,更好的模型泛化能力等等。
4. LayerNorm是后起之秀,挑战前辈BatchNorm必然是解决它的某些痛点或者劣势,那么BatchNorm有哪些痛点呢?
- batch非常小,比如训练资源有限无法应用较大的batch,也比如在线学习等使用单例进行模型参数更新的场景
- 对于rnn等动态的网络结构,同一个batch中训练实例有长有短,导致每一个时间步长必须维持各自的统计量,这使得BN并不能正确的使用。
5. 约定俗称,比如NLP几个经典模型都是用的LayerNorm,之后很多的追随者也沿用了这一套。
另外需要注意的一个点是由于现在训练模型都是采用的mini-batch的方式,所以在batchnorm在估计训练集(推理阶段)整体的均值方差时,常采用EMA( exponential moving average),指数移动平均来估计:
其中和
为训练阶段的均值和方差,
然后对特征进行归一化,
除了归一化,BatchNorm还包括对各个channel的特征做affine tranform(增加特征表达能力,有待考证):
和
都是可训练的参数。
四、RMS Norm和Deep Norm
RMS:Root Mean Square Layer Normalization
与layerNorm相比,RMS Norm的主要区别在于去掉了减去均值的部分,计算公式为:
, 其中
1、可以在梯度下降时令损失更加平滑?(有待考证)?
2、可以在各个模型上减少约 7%∼64% 的计算时间。
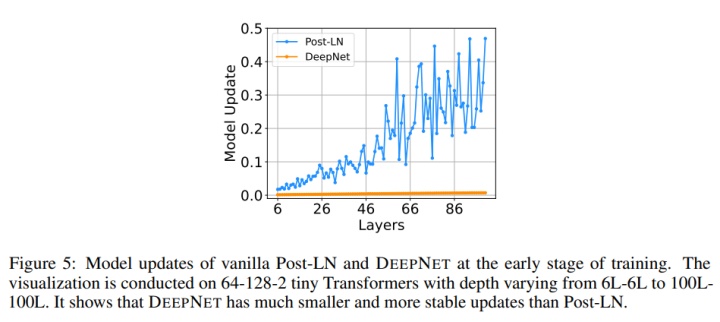
Deep Norm是对Post-LN的的改进,代码如下,

作者认为 Post-LN 的不稳定性部分来自于梯度消失以及太大的模型更新,而DeepNorm可以缓解这个问题
- DeepNorm在进行Layer Norm之前会以
参数扩大残差连接
- 在Xavier参数初始化过程中以
减小部分参数的初始化范围
说一千道一万,对于没法做到理论功底那么深厚的人来说,效果为王,谁效果好就用谁
五、参考资料
-
DEEPNORM:千层transformer...
-
昇腾大模型|结构组件-1——Layer Norm、RMS Norm、Deep Norm
-
BatchNorm与LayerNorm
-
BatchNorm与LayerNorm的理解