RNN，LSTM和GRU细胞。

        如果你想对顺序或时间序列数据（例如，文本、音频等）进行预测，传统的神经网络是一个糟糕的选择。但是为什么？

        在时间序列数据中，当前观测值依赖于先前的观测值，因此观测值并非彼此独立。然而，传统的神经网络认为每个观察都是独立的，因为网络无法保留过去或历史信息。基本上，他们对过去发生的事情没有记忆。

        这导致了递归神经网络（RNN）的兴起，它通过包括数据点之间的依赖关系将记忆的概念引入神经网络。有了这个，可以训练RNN根据上下文记住概念，即学习重复的模式。

        但是RNN是如何实现这种记忆的呢？

        RNN通过细胞中的反馈回路实现记忆。这是RNN和传统神经网络之间的主要区别。反馈循环允许信息在层内传递，而前馈神经网络则信息仅在层之间传递。

        然后，RNN必须定义哪些信息足够相关以保留在内存中。为此，进化了不同类型的RNN：

• 传统递归神经网络 （RNN）
• 长期短期记忆循环神经网络 （LSTM）
• 门控循环单元循环神经网络 （GRU）

        在本文中，我将向您介绍RNN，LSTM和GRU。我将向您展示它们的异同以及一些优点和缺点。除了理论基础之外，我还向您展示了如何使用 在 Python 中实现每种方法。tensorflow

三、递归神经网络 （RNN）

        通过反馈循环，一个RNN单元的输出也用作同一单元的输入。因此，每个单元格有两个输入：过去和现在。使用过去的信息会导致短期记忆。

        为了更好地理解，我们展开/展开RNN细胞的反馈回路。展开单元格的长度等于输入序列的时间步长数。

展开的递归神经网络。

        我们可以看到过去的观察结果是如何作为隐藏状态通过展开的网络传递的。在每个单元格中，当前时间步长x（现值）、前一时间步的隐藏状态h（过去值）和偏差的输入被组合在一起，然后通过激活函数进行限制，以确定当前时间步的隐藏状态。

        在这里，粗体小字母表示向量，而大写粗体字母表示矩阵。

        RNN 的权重 W 通过反向时间传播 （BPTT） 算法进行更新。

        RNN 可用于一对一、一对多、多对一和多对多预测。

3.1 RNN 的优势

        由于其短期记忆，RNN可以处理顺序数据并识别历史数据中的模式。此外，RNN能够处理不同长度的输入。

3.2 RNN的缺点

        RNN遭受消失梯度下降的影响。在这种情况下，用于在反向传播期间更新权重的梯度变得非常小。将权重与接近零的梯度相乘会阻止网络学习新的权重。这种学习的停止导致RNN忘记了在较长的序列中看到的内容。梯度下降消失的问题随着网络的层数增加。

        由于RNN只保留最近的信息，因此模型在考虑遥远过去的观察结果方面存在问题。因此，RNN倾向于在长序列上丢失信息，因为它只存储最新的信息。因此，RNN只有短期记忆，而不是长期记忆。

        此外，由于RNN及时使用反向传播来更新权重，网络也受到梯度爆炸的影响，如果使用ReLu激活函数，则会出现死ReLu单元。前者可能导致收敛问题，而后者可能会停止学习。

3.3 RNN在张量流中的实现

        我们可以使用 .为此，我们使用允许我们堆叠 RNN 层的模型，即层类和层类。tensorflowSequentialSimpleRNNDense

from tensorflow.keras import Sequential
from tensorflow.keras.layers import SimpleRNN, Dense
from tensorflow.keras.optimizers import Adam

        只要我们想使用默认参数，就不需要导入优化器。但是，如果我们想自定义优化器的任何参数，我们还需要导入优化器。

        为了构建网络，我们定义一个模型，然后使用该方法添加RNN层。为了添加 RNN 层，我们使用类和传递参数，例如单元数、辍学率或激活函数。对于第一层，我们还可以传递输入序列的形状。Sequentialadd()SimpleRNN

        如果我们堆叠RNN层，我们需要将前一层的参数设置为。这可确保层的输出具有下一个 RNN 层的正确格式。return_sequenceTrue

        为了生成输出，我们使用一个层作为我们的最后一层，传递输出的数量。Dense

# define parameters
n_timesteps, n_features, n_outputs = X_train.shape[1], X_train.shape[2], y_train.shape[1]# define model
rnn_model = Sequential()
rnn_model.add(SimpleRNN(130, dropout=0.2, return_sequences=True, input_shape=(n_timesteps, n_features)))
rnn_model.add(SimpleRNN(110, dropout=0.2, activation="tanh", return_sequences=True))
rnn_model.add(SimpleRNN(130, dropout=0.2, activation="tanh", return_sequences=True))
rnn_model.add(SimpleRNN(100, dropout=0.2, activation="sigmoid", return_sequences=True))
rnn_model.add(SimpleRNN(40, dropout=0.3, activation="tanh"))
rnn_model.add(Dense(n_outputs))

        定义 RNN 后，我们可以使用该方法编译模型。在这里，我们传递损失函数和我们要使用的优化器。 提供一些内置的损失函数和优化器。compile()tensorflow

rnn_model.compile(loss='mean_squared_error', optimizer=Adam(learning_rate=0.001))

在训练 RNN 之前，我们可以使用该方法查看模型和参数数量。这可以让我们了解模型的复杂性。summary()

我们使用该方法训练模型。在这里，我们需要传递训练数据和不同的参数来自定义训练，包括 epoch 数、批量大小、验证拆分和提前停止。fit()

stop_early = tf.keras.callbacks.EarlyStopping(monitor='val_loss', patience=5)
rnn_model.fit(X_train, y_train, epochs=30, batch_size=32, validation_split=0.2, callbacks=[stop_early])

        要对我们的测试数据集或任何看不见的数据进行预测，我们可以使用该方法。该参数仅说明我们是否要获取有关预测过程状态的任何信息。在这种情况下，我不希望打印出任何状态。predict()verbose

y_pred = rnn_model.predict(X_test, verbose=0)

张量流中 RNN 的超参数调优

        正如我们所看到的，RNN的实现非常简单。然而，找到正确的超参数，例如每层的单元数、辍学率或激活函数，要困难得多。

        但是，我们可以使用库，而不是手动更改超参数。该库有四个调谐器、、 和 ，用于从给定的搜索空间中识别正确的超参数组合。keras-tunerRandomSearchHyperbandBayesianOptimizationSklearn

        要运行调谐器，我们首先需要导入和 Keras 调谐器。tensorflow

import tensorflow as tf
import keras_tuner as kt

然后，我们构建超调谐模型，在其中定义超参数搜索空间。我们可以使用一个函数构建超模型，在该函数中，我们以与上述相同的方式构建模型。唯一的区别是我们为要调整的每个超参数添加搜索空间。在下面的示例中，我想调整每个 RNN 层的单元数、激活函数和辍学率。

def build_RNN_model(hp):# define parametersn_timesteps, n_features, n_outputs = X_train.shape[1], X_train.shape[2], y_train.shape[1]# define modelmodel = Sequential()model.add(SimpleRNN(hp.Int('input_unit',min_value=50,max_value=150,step=20), return_sequences=True, dropout=hp.Float('in_dropout',min_value=0,max_value=.5,step=0.1), input_shape=(n_timesteps, n_features)))model.add(SimpleRNN(hp.Int('layer 1',min_value=50,max_value=150,step=20), activation=hp.Choice("l1_activation", values=["tanh", "relu", "sigmoid"]), dropout=hp.Float('l1_dropout',min_value=0,max_value=.5,step=0.1), return_sequences=True))model.add(SimpleRNN(hp.Int('layer 2',min_value=50,max_value=150,step=20), activation=hp.Choice("l2_activation", values=["tanh", "relu", "sigmoid"]), dropout=hp.Float('l2_dropout',min_value=0,max_value=.5,step=0.1), return_sequences=True))model.add(SimpleRNN(hp.Int('layer 3',min_value=20,max_value=150,step=20), activation=hp.Choice("l3_activation", values=["tanh", "relu", "sigmoid"]), dropout=hp.Float('l3_dropout',min_value=0,max_value=.5,step=0.1), return_sequences=True))model.add(SimpleRNN(hp.Int('layer 4',min_value=20,max_value=150,step=20), activation=hp.Choice("l4_activation", values=["tanh", "relu", "sigmoid"]), dropout=hp.Float('l4_dropout',min_value=0,max_value=.5,step=0.1)))# output layermodel.add(Dense(n_outputs))model.compile(loss='mean_squared_error', optimizer=Adam(learning_rate=1e-3))return model

        要定义每个变量的搜索空间，我们可以使用不同的方法，例如、 和 。前两者的用法非常相似。我们给它们一个名称、一个最小值、一个最大值和一个步长。该名称用于标识超参数，而最小值和最大值定义我们的值范围。步长参数定义了我们用于调优的范围内的值。可用于调整分类超参数，例如激活函数。在这里，我们只需要传递要测试的选项列表。hp.Inthp.Floathp.Choicehp.Choice

        构建超模型后，我们需要实例化调谐器并执行超调谐。尽管我们可以在不同的调优算法之间进行选择，但它们的实例化非常相似。我们通常需要指定要优化的目标和要训练的最大 epoch 数。在这里，建议将 epochs 设置为略高于我们预期的 epoch 数的数字，然后使用提前停止。

        例如，如果我们想使用调谐器和验证损失作为目标，我们可以将调谐器构建为Hyperband

tuner = kt.Hyperband(build_RNN_model,objective="val_loss",max_epochs=100,factor=3,hyperband_iterations=5,directory='kt_dir',project_name='rnn',overwrite=True)

        在这里，我还传递了存储结果的目录，以及调谐器迭代完整超带算法的频率。

        实例化调谐器后，我们可以使用该方法执行超参数调优。search()

stop_early = tf.keras.callbacks.EarlyStopping(monitor='val_loss', patience=5)
tuner.search(X_train, y_train, validation_split=0.2, callbacks=[stop_early])

为了提取最佳超参数，我们可以使用该方法并使用我们调整的每个超参数的方法和名称。get_best_hyperparameters()get()

best_hps=tuner.get_best_hyperparameters(num_trials=1)[0]
print(f"input: {best_hps.get('input_unit')}")
print(f"input dropout: {best_hps.get('in_dropout')}")

四、长期短期记忆 （LSTM）

LSTM是一种特殊类型的RNN，它解决了简单RNN的主要问题，即梯度消失的问题，即过去进一步的信息丢失。

展开的长短期记忆细胞。

LSTM 的关键是单元状态，它从单元的输入传递到输出。因此，细胞状态允许信息沿着整个链流动，只需通过三个门的微小线性动作。因此，细胞状态代表 LSTM 的长期记忆。这三个门称为遗忘门、输入门和输出门。这些门用作过滤器并控制信息流，并确定保留或忽略哪些信息。

遗忘门决定保留多少长期记忆。为此，使用了一个sigmoid函数来说明细胞状态的重要性。输出在 0 到 1 之间变化，并说明保留了多少信息，即 0，不保留任何信息，1，保留单元格状态的所有信息。输出由当前输入x、前一个时间步的隐藏状态h和偏置b组合确定。

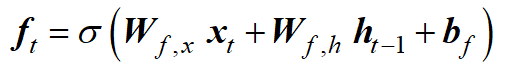
输入门决定将哪些信息添加到细胞状态中，从而添加到长期记忆中。在这里，sigmoid 层决定更新哪些值。

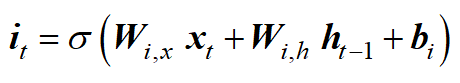
输出门决定单元状态的哪些部分构建输出。因此，输出门负责短期记忆。

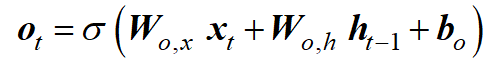
可以看出，所有三个门都由相同的功能表示。只有权重和偏差不同。单元格状态通过遗忘门和输入门更新。

上述等式中的第一个项决定了保留了多少长期记忆，而第二项则向细胞状态添加新信息。

然后，当前时间步长的隐藏状态由输出门和将单元状态限制在 -1 和 1 之间的 tanh 函数确定。

4.1 LSTM的优势

LSTM的优点与RNN相似，主要优点是它们可以捕获序列的长期和短期模式。因此，它们是最常用的RNN。

4.2 LSTM的缺点

由于其更复杂的结构，LSTM 的计算成本更高，导致训练时间更长。

由于 LSTM 还使用时间反向传播算法来更新权重，因此 LSTM 存在反向传播的缺点（例如，死 ReLu 元素、梯度爆炸）。

4.3 LSTM在张量流中的实现

        LSTM的实现与简单的RNN非常相似。唯一的区别是我们导入类而不是类。tensorflowLSTMSimpleRNN

from tensorflow.keras import Sequential
from tensorflow.keras.layers import LSTM, Dense
from tensorflow.keras.optimizers import Adam

我们可以像简单的RNN一样将LSTM网络组合在一起。

# define parameters
n_timesteps, n_features, n_outputs = X_train.shape[1], X_train.shape[2], y_train.shape[1]# define model
lstm_model = Sequential()
lstm_model.add(LSTM(130, return_sequences=True, dropout=0.2, input_shape=(n_timesteps, n_features)))
lstm_model.add(LSTM(70, activation="relu", dropout=0.1, return_sequences=True))
lstm_model.add(LSTM(100, activation="tanh", dropout=0))# output layer
lstm_model.add(Dense(n_outputs, activation="tanh"))lstm_model.compile(loss='mean_squared_error', optimizer=Adam(learning_rate=0.001))stop_early = tf.keras.callbacks.EarlyStopping(monitor='val_loss', patience=5)
lstm_model.fit(X_train, y_train, epochs=30, batch_size=32, validation_split=0.2, callbacks=[stop_early])

        超参数调整也与简单 RNN 相同。因此，我们只需要对我上面显示的代码片段进行微小的更改。

五、门控循环单元 （GRU）

        与LSTM类似，GRU解决了简单RNN的梯度消失问题。然而，与LSTM的区别在于GRU使用较少的门，并且没有单独的内部存储器，即单元状态。因此，GRU 仅依靠隐藏状态作为内存，从而简化架构。

展开的门控循环单元 （GRU）。

        复位门负责短期记忆，因为它决定保留和忽略多少过去的信息。

        向量 r 中的值由 sigmoid 函数限定在 0 和 1 之间，并取决于前一个时间步长的隐藏状态 h 和当前输入 x。两者都使用权重矩阵 W 进行加权。此外，还添加了偏差 b。

        相比之下，更新门负责长期记忆，可与LSTM的遗忘门相媲美。

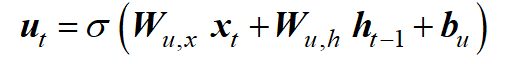
        正如我们所看到的，重置门和更新门之间的唯一区别是权重 W。

        当前时间步的隐藏状态是根据两步过程确定的。首先，确定候选隐藏状态。候选状态是当前输入和前一个时间步的隐藏状态以及激活函数的组合。在此示例中，使用 tanh 函数。先前隐藏状态对候选隐藏状态的影响由复位门控制

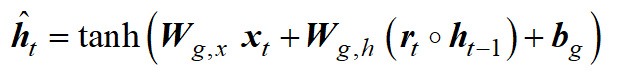
        在第二步中，将候选隐藏状态与前一个时间步的隐藏状态相结合，以生成当前隐藏状态。以前的隐藏状态和候选隐藏状态的组合方式由更新入口确定。

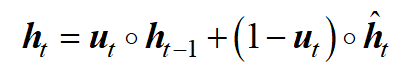
        如果更新门给出的值为 0，则完全忽略以前的隐藏状态，当前隐藏状态等于候选隐藏状态。如果更新门给出的值为 <>，反之亦然。

5.1 GRU 的优势

        由于与 LSTM 相比架构更简单（即两个而不是三个门和一个状态而不是两个），GRU 在计算上更有效率，训练速度更快，因为它们需要更少的内存。

        此外，GRU已被证明对较小的序列更有效。

5.2 GRU 的缺点

        由于GRU没有单独的隐藏和细胞状态，它们可能无法像LSTM那样考虑过去的观测结果。

        与RNN和LSTM类似，GRU也可能遭受反向传播的缺点，及时更新权重，即死ReLu元素，爆炸梯度。

5.3 GRU在张量流中的实现

        至于LSTM，GRU的实现与简单的RNN非常相似。我们只需要导入类，而其余部分保持不变。GRU

from tensorflow.keras import Sequential
from tensorflow.keras.layers import GRU, Dense
from tensorflow.keras.optimizers import Adam# define parameters
n_timesteps, n_features, n_outputs = X_train.shape[1], X_train.shape[2], y_train.shape[1]# define model
gru_model = Sequential()
gru_model.add(GRU(90,return_sequences=True, dropout=0.2, input_shape=(n_timesteps, n_features)))
gru_model.add(GRU(150, activation="tanh", dropout=0.2, return_sequences=True))
gru_model.add(GRU(60, activation="relu", dropout=0.5))
gru_model.add(Dense(n_outputs))gru_model.compile(loss='mean_squared_error', optimizer=Adam(learning_rate=0.001))stop_early = tf.keras.callbacks.EarlyStopping(monitor='val_loss', patience=5)
gru_model.fit(X_train, y_train, epochs=30, batch_size=32, validation_split=0.2, callbacks=[stop_early])

这同样适用于超参数优化。

六、结论

        递归神经网络将记忆引入神经网络。这样，观测值在顺序和时间序列数据中的依赖性就包含在我们的预测中。

        在本文中，我向您展示了三种类型的递归神经网络，即简单RNN，LSTM和GRU。我已经向您展示了它们是如何工作的，它们的优点和缺点是什么，以及如何使用 在 Python 中实现它们。tensorflow

        请让我知道您对这篇文章的看法！