可能有人要问：求交点坐标有什么用呢？而且为啥要用线代来求？直线方程不行吗？？？

        这个问题，我只能说，直线方程计算的次数过多了，而且动不动就要考虑线的方向，90°的直线的斜率不存在，所以用向量（也就是线性代数）来算更好点。至于有什么用处，也许一些算法需要吧，比如计算一线是否与矩形相交来进行判定。

        本教程涉及线代的内容较少，除了思想，你还会学到：

        如何判断两线段是否相交？相似三角形的性质。一点到另一点的方向。三角函数相关知识。

        还有，向量叉乘的正负特性，向量叉乘的计算，单位向量的计算，一点至另一点的向量表示方法，向量的数量积（点积）的几何意义与计算。

---

线性代数的运用举例：

1. 求交点（本教程）
2. 将凹多边形分为三角形（用于渲染）
3. 距离一条直线最短的点（叉乘）
4. 各种方向判断问题。

---

Part 1:怎样判断线段是否相交？

        此部分需要先理解向量叉乘的意义，我先通俗地讲一下

        首先，看下图。

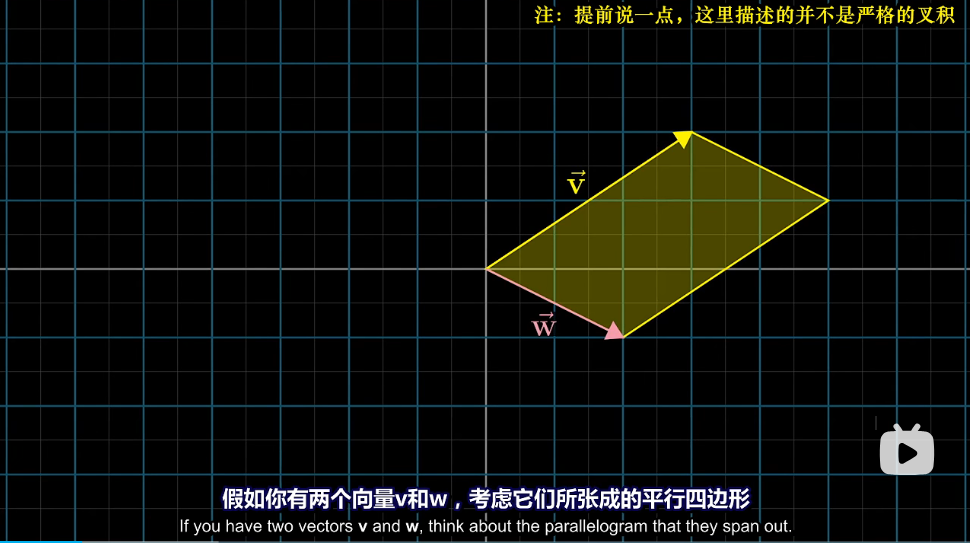
        我们有两个向量v与向量w，那么v（向量两字省略，后面也是如此）与w所形成的平行四边形的面积，就是v×w的结果（×即为叉乘），但是叉乘具有正负性，

        如果v在w的左边，那么v×w＜0（也就是负的），

        如果v在w的右边，那么v×w＞0（也就是正的），

        当v与w重合或相反，很容易想到结果是0（没有张成平行四边形），

        总结一下，顺时针负，逆时针正。

        对了，对于一个向量[x1,y1]与向量[x2,y2]，他们的叉乘就是这两个向量的行列式（这句可以看不懂），也就是x1*y2-x2*y1。

---

        根据以上结论，我们就可以开始研究两条线怎样才会相交。

相交示意图

        如图，线段AB与线段CD相交，连接AB的端点到CD形成向量a，b，c，d。

        我们发现，a叉乘b的结果与d叉乘c异号。

        再来看不相交的。

不相交示意图

        向量a叉乘b与d叉乘c的的符号一样

        接下来看看特殊的。

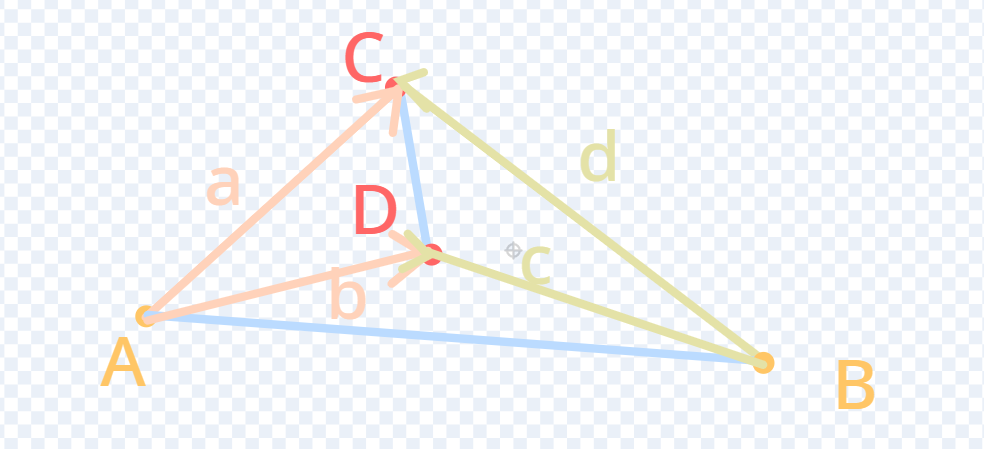
特殊的不相交

        这次a叉乘b与d叉乘c的符号不同，这种错误要把d与b互换就行了，如下图：

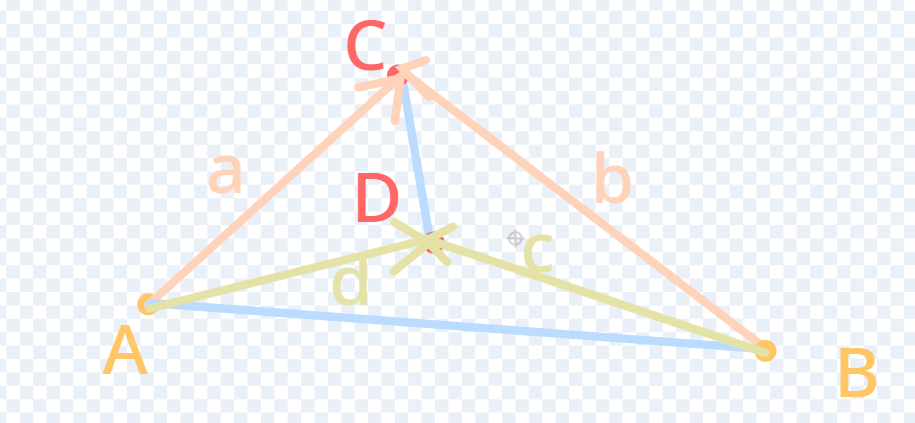
        更正后的（注意向量叉乘时要让端点在同一个地方。

        这回，a叉乘b与d叉乘c的符号又相同了！

        总结一下，若a(x1,y1),b(x2,y2),c(x3,y3),d(x4,y4)，（都是向量）那么上面的一大堆用数学来表示就是下面这个图：

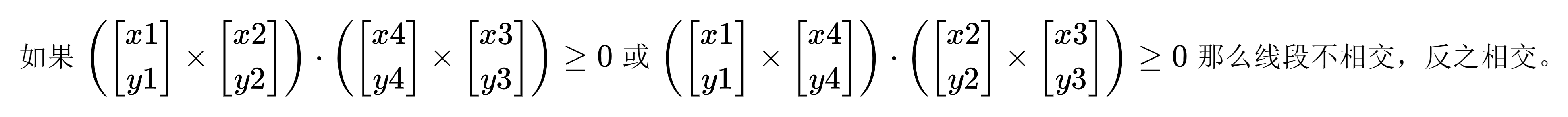
        上图中，×代表叉乘，·代表乘法，相乘大于等于就是同号的意思啦。

        或者把“或”改为“与”，然后把≥改为＜，那么线段就相交，反之不相交。

---

接下来开始用代码实现！

        这里呢，我先简简单单地做了一个绘制系统：

然后，创建一个自制积木

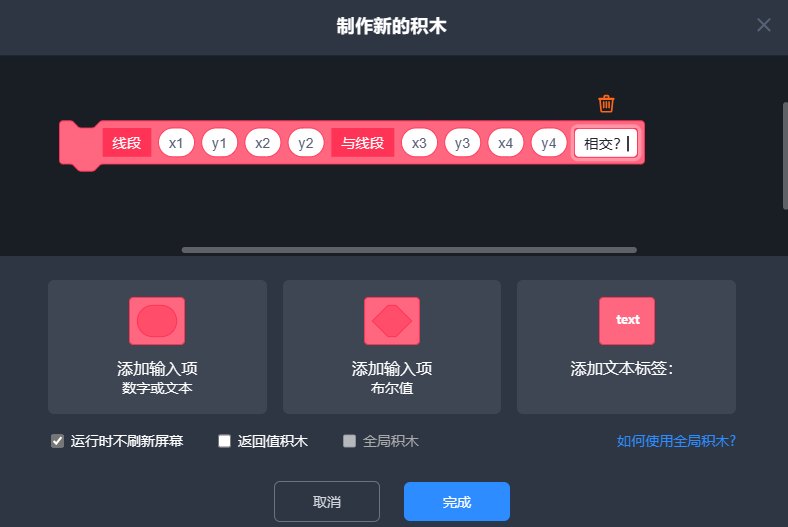
        那么，我们就可以写下这样的代码，来实现判断两线段是否相交：先计算a，b，c，d的向量，然后根据叉乘公式（别忘了，就是行列式：x1*y2-x2*y1），进行判断。

        那向量怎么求呢？

        这个问题有个公式，对于在平面直角坐标系内的点A(x1,y1)与点B(x2,y2)，向量AB即为[(x2-x1),(y2-y1)]

        我们直接上代码。

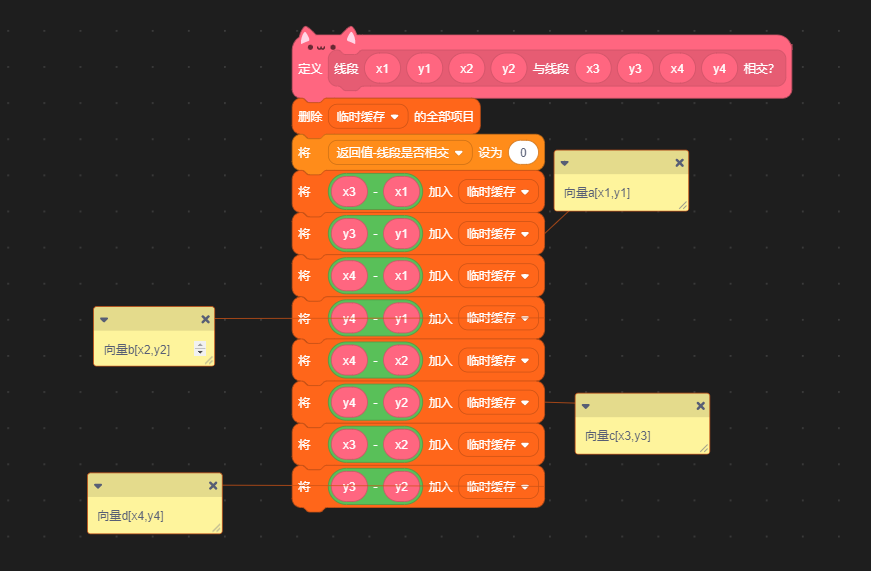
计算向量

        首先是计算向量，然后保存在缓存里面，并且初始化返回值。接下来我们要进行叉乘，并且判断是否＜0，如下图：

叉乘并判断

        这样，一个香蕉 相交判断就做完力，可要是判断线段是否在线上，那该怎么弄呢？

        我们知道，如果一个向量与另一个向量的夹角为0°或者180°，那么他们的叉乘为0。在线上时，两个向量分别指向另外两个端点，就形成了180度；

        如果这个点在另条线段的延长线上，那么这两个向量的夹角是0°；

        那如果点在端点上呢？

        想想看，那么一个向量的模长（长度）就是0了，好像怎么叉乘还是0。

        那么这3种可能都会出现叉乘为0，我们就可以加上等于0的判断，返回相应的值。，如下图：

---

Part 2：计算交点

        部分1总算是写完了，接下来便是交点坐标的计算。

1.理清思路。

线段AB与CD交于点E

        如图，点H为C投影至AB的点，G同理。（投影就是向它做垂线），投影长度分别为d1，d2。

        我们要求的是点E的坐标，为此，我先讲一下：什么是相似三角形？（六年级即可懂，初三及以上学生请跳过）

两个三角形

        如图，AB平行于CF平行于DE，由于平行线，我们知道图中有大多相同的角，都已经标在图中。

        我们观察一下，这两个三角形三个角（或者两个）是一样的（真的），但是他们并不全等，像这样三个角都相等的两个三角形，我们称它们相似（不知道准不准确啊，我才初一（）

        对于两个相似三角形，它们的对应边长的比值都是相等的。比如：

        AB/BC=DE/DC , AB/DE=AC/CE。

        不知道你有没有看懂，反正就这些了。

再来看刚刚的图：

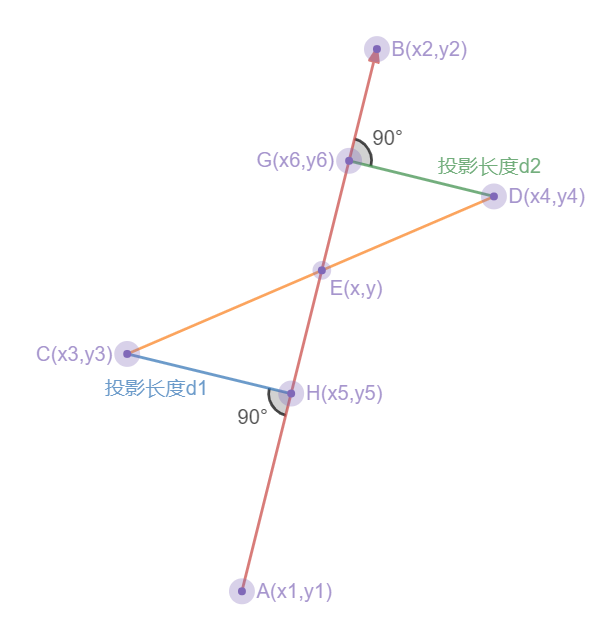
求交点E的坐标

        首先，我们看三角形DGE与三角形CHE，由于俩对顶角相等（∠CEH与∠GED），而且由于是投影，所以有个角都是90度，所以，这两个三角形相似。

        相似？那就是比值相等呗！那不就是交点(x, y)距离两点的比例则和d1, d2的比例相同吗？（d1/d2=EH/GE）

        我们看看，EH占GH的几分之几呢？是EH/GH吧，现在，由于比例相同，我们可以把EH/GH写成d1/(d1+d2)的形式{也就是EH/GH=EH/(EH+GE)=d1/(d1+d2)}。

        同理，GE/GH也能写成d2/(d1+d2)的形式{也就是GE/GH=GE/(EH+GE)=d2/(d1+d2)}。

        哎，权重（占比）知道了，坐标不就好办了嘛！(x,y)就是 H坐标*占比+G坐标*占比啊，即

注意权重不要写反了

---

2.计算投影。

        你肯定要问我：d1，d2咋算啊？？？还有，你投影坐标是个啥？？？

        这就要说一下向量点积（·）的几何意义了。

向量点积示意图

        向量点积的几何意义是，一个向量向另一向量投影，然后再乘上另一向量的长度（模长）之后的点与端点的距离。在图中，向量AB·向量AD得到AE的长度，即AC*AD。

        坐向量点积公式1（坐标系）：a·b=(x1，y1)·(x2，y2)=x1*x2+y1*y2。其中，a和b分别为两个向量，(x1，y1)和(x2，y2)

        向量点积公式2（几何）：a·b=|a|*|b|*cosθ,θ是a,b的夹角

        向量叉乘公式（几何）：a·b=|a|*|b|*sinθ,θ是a,b的夹角

        哎，我们发现有个投影！那如果上面公式中b的模长（长度）为1呢？

        由于点积的几何意义，当b的模长为1时，a·b就是a向b的投影！

        那我们就可以计算投影了。

“投影”

        给定一个直线外点(x0, y0)和直线上两点(x1, y1), (x2, y2)，计算投影点(x, y)。

        如何把向量AB投影至向量AC？

        首先，求出AC的单位向量（模长为1，紫色），然后向量AB·紫色向量，就得到了AD的长度，最后，求出AC的方向，在AC方向上移动AD长度，就是点D的坐标啦。（耶）

        至于AC方向怎么求，可以用反三角函数——arctan来求，这里不多说，直接上代码。

        接下来，怎么求出单位向量？

        对于一个向量[x,y]它的单位向量是[x/√(x^2+y^2),y/√(x^2+y^2)]，其实就是向量除以模长。如下图：

单位向量公式

        那么就剩点积了。

点积

        接下来我们就可以计算投影了。

一半的投影（由于可能要用缓存，所以使用的是倒数第1和2项）

        啊，我们求出AD长度和方向，但怎么知道他的横纵坐标呢？

求A'B与BD

        这是刚刚那幅图的一部分，我们要求的是AB的x长度和y长度（横纵坐标差），也就是A'B与BD

        因为∠AA'B=90°，所以三角形AA'B为直角三角形

        对于直角三角形，我们有一个定理：每个角度的三角形三个边都有一个固定的比值。

        也就是说，在三角形AA'B中，A'B/AB与AA'（长度也就是BD）/AB的值是固定的。

        在这里，我们把AA'叫做角a的邻边，A'B叫做角a的对边，AB叫做角a的斜边。（可以不记住）

        我们把对边与斜边的比叫做正弦，记作sin，即sin a=对/斜；

        邻边与斜边的比值叫做余弦，记作cos，即cos a=邻/斜;

        还有正切（tan）和反三角等函数，感兴趣的可以自己搜，我们这次只用sin和cos。

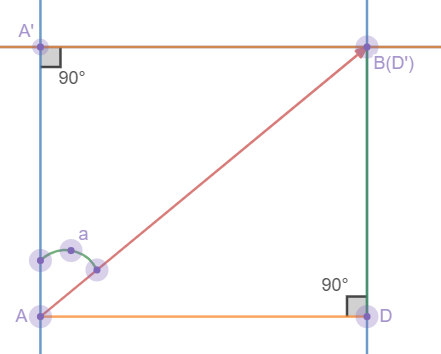
        我们知道AB与角a的值了，那A'B和A'A就很好求了，

        sin a=A'B/AB，AB*sin a=A'B/AB*AB=A'B（求出来了！）

        cos a=A'A/AB，AB*cos a=A'A/AB*AB=A'A

        那么横纵坐标差也就求出来了，代码如下所示：

投影

        不要忘记还要算出投影距离（勾股定理）

        最终代码如图所示

        更改绘制代码

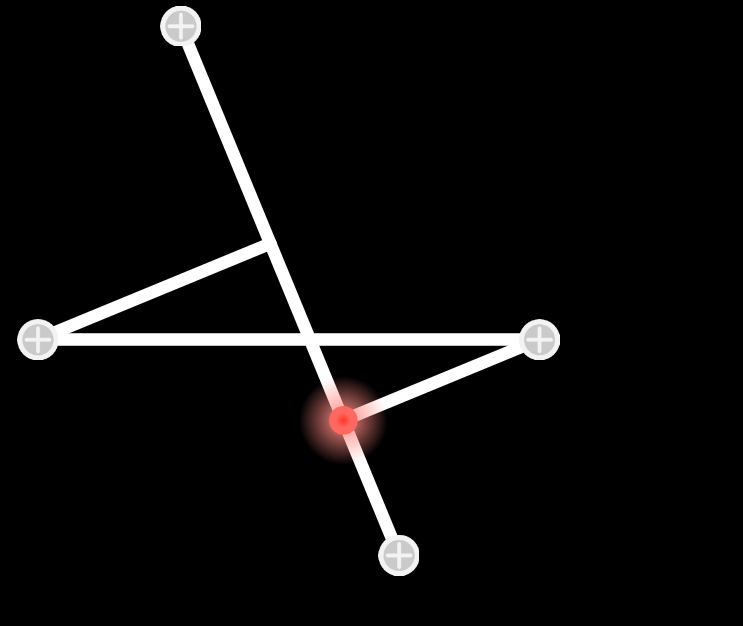
图像

        我们发现投影是个垂线，说明程序正常。（在做程序时要养成检测的习惯！）wonderful！

---

3.计算交点坐标

刚刚推出的公式

        这是我们刚刚推出的交点坐标公式，在这里，d1，d2和x6，y6，x5，y5我们都可以算出来，那么x，y也就出来了！

        首先，我们要先把一个线段投影到另一个线段上

线段交点坐标的一部分

        然后，算出每个点的权重（就是d1 d2那个）：

线段交点坐标的一部分*2

        最后，将权重与点坐标相乘并相加，即为相交点坐标。

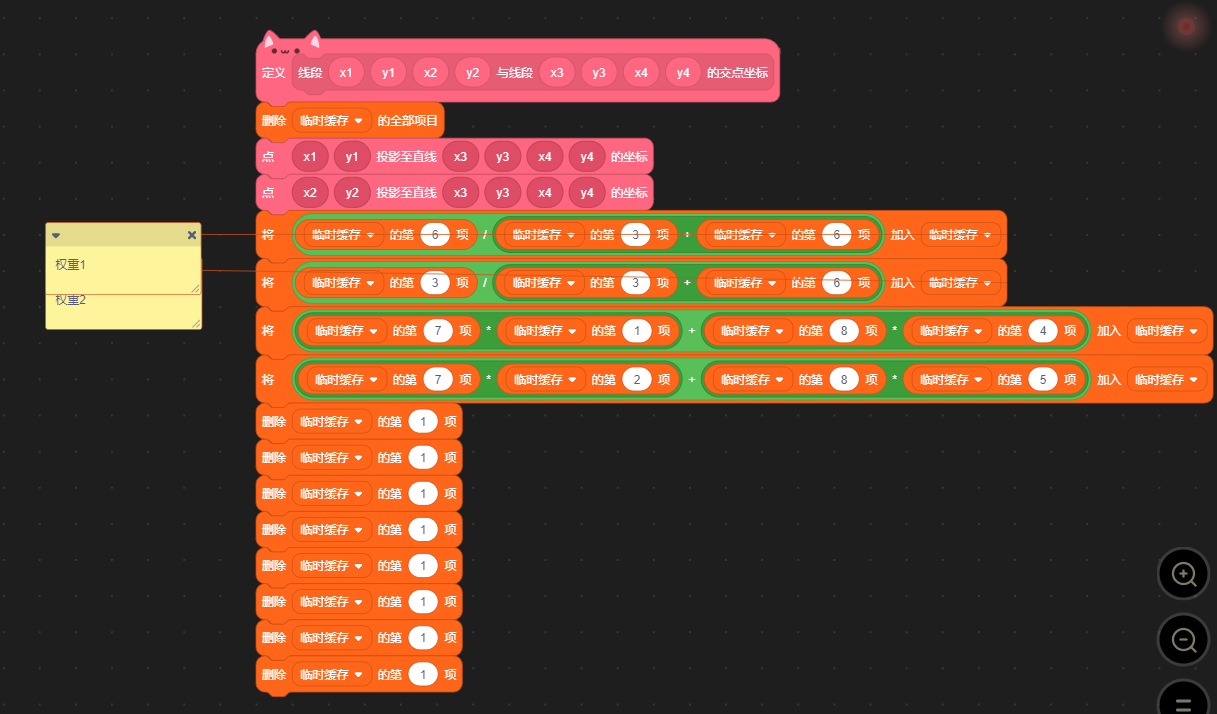
线段交点坐标（全）

---

Part 3：结尾

        到此，两个线段的交点坐标已经做完了，以下是全部代码：

所有代码

        在绘制与移动区域内，我添加了透明度变化，防止混淆。

        我们来测试一下。

效果展示

---

资源下载链接

        不想写代码的，可以下载这个配套资源：Scratch 教程作品：线段交点坐标

        感谢支持