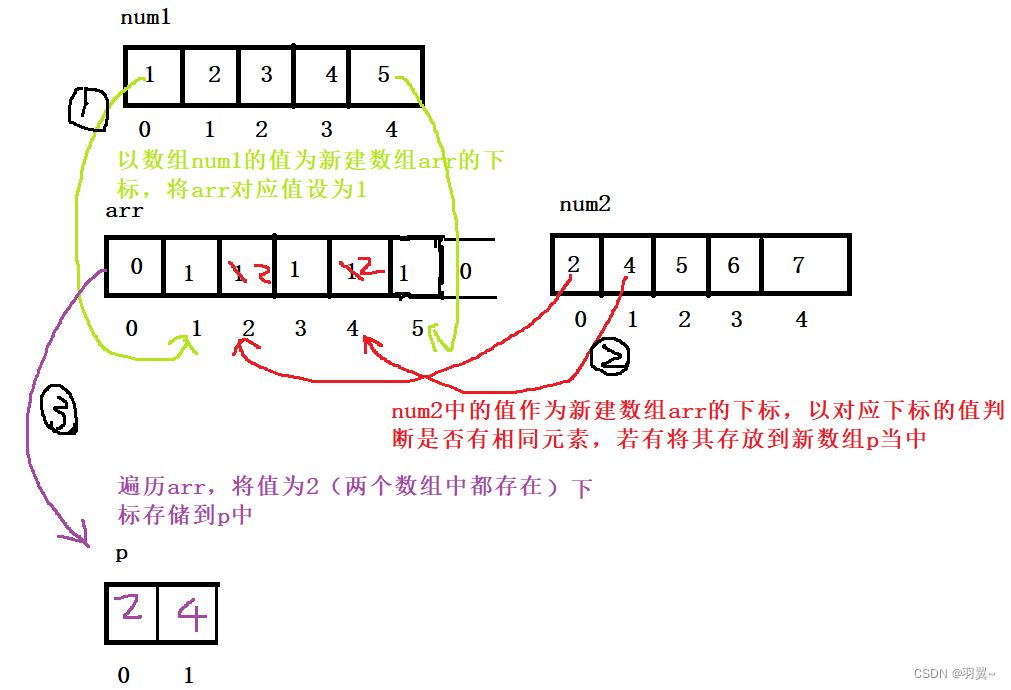
N 个皇后

问题描述

将n个皇后放在n大小的棋盘上，没有两个皇后可以互相攻击。 最常见的 n 个皇后谜题是八个皇后谜题，n = 8：

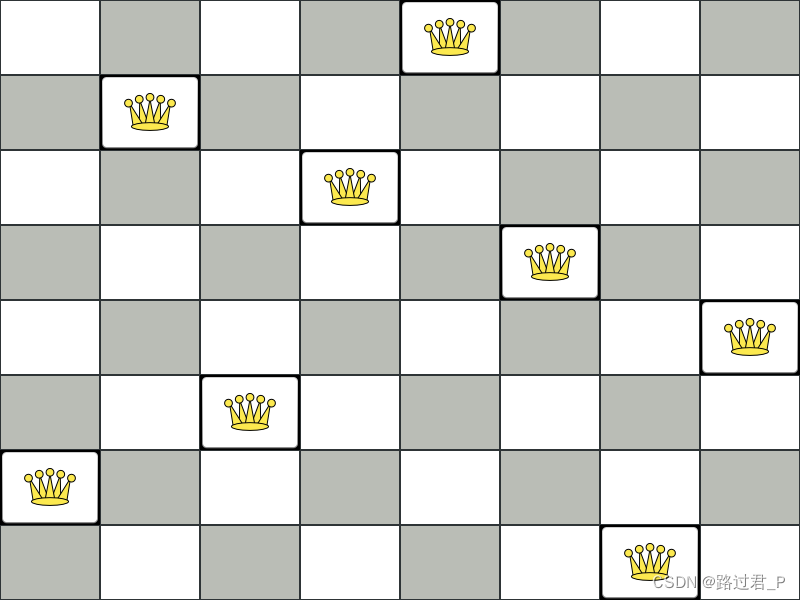
约束：

• 使用 n 列和 n 行的棋盘。
• 在棋盘上放置n个皇后。
• 没有两个女王可以互相攻击。女王可以攻击同一水平线、垂直线或对角线上的任何其他女王。

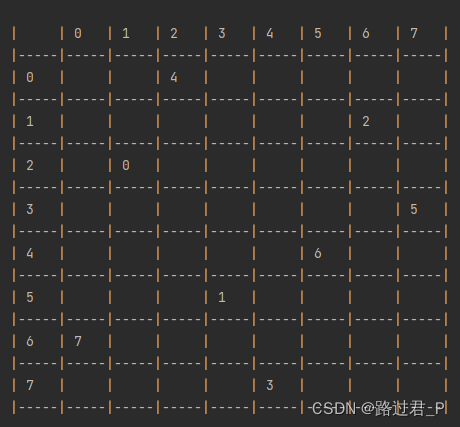
求解结果（time limit 5s）

问题大小

n	搜索空间
4	256
8	10^7
16	10^19
32	10^48
64	10^115
256	10^616

域模型

@Data
@AllArgsConstructor
public class Column {private int index;
}
@Data
@AllArgsConstructor
public class Row {private int index;
}
@Data
@AllArgsConstructor
@NoArgsConstructor
@PlanningEntity
public class Queen {@PlanningIdprivate Integer id;@PlanningVariableprivate Column column;@PlanningVariableprivate Row row;// 升序对角线索引（左上到右下）public int getAscendingDiagonalIndex() {return column.getIndex() + row.getIndex();}// 降序对角线索引（左下到右上）public int getDescendingDiagonalIndex() {return column.getIndex() - row.getIndex();}
}
@Data
@AllArgsConstructor
@NoArgsConstructor
@PlanningSolution
public class NQueen {@ValueRangeProvider@ProblemFactCollectionPropertyprivate List<Column> columnList;@ValueRangeProvider@ProblemFactCollectionPropertyprivate List<Row> rowList;@PlanningEntityCollectionPropertyprivate List<Queen> queenList;@PlanningScoreprivate HardSoftScore score;
}

例如：

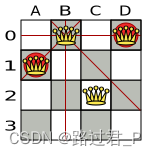
Queen	Column	Row	AscendingDiagonalIndex	DescendingDiagonalIndex
A1	0	1	1 (**)	-1
B0	1	0 (*)	1 (**)	1
C2	2	2	4	0
D0	3	0 (*)	3	3

(*)(**)的皇后可以互相攻击

求解器（约束提供者）

public class NQueenConstraintProvider implements ConstraintProvider {@Overridepublic Constraint[] defineConstraints(ConstraintFactory constraintFactory) {return new Constraint[]{// 列冲突columnConflict(constraintFactory),// 行冲突rowConflict(constraintFactory),// 升序对角线冲突ascendingDiagonalIndexConflict(constraintFactory),// 降序对角线冲突descendingDiagonalIndexConflict(constraintFactory),};}public Constraint columnConflict(ConstraintFactory constraintFactory) {return constraintFactory.forEach(Queen.class).join(Queen.class,Joiners.equal(Queen::getColumn),Joiners.lessThan(Queen::getId)).penalize(HardSoftScore.ONE_HARD).asConstraint("Column conflict");}public Constraint rowConflict(ConstraintFactory constraintFactory) {return constraintFactory.forEach(Queen.class).join(Queen.class,Joiners.equal(Queen::getRow),Joiners.lessThan(Queen::getId)).penalize(HardSoftScore.ONE_HARD).asConstraint("Row conflict");}public Constraint ascendingDiagonalIndexConflict(ConstraintFactory constraintFactory) {return constraintFactory.forEach(Queen.class).join(Queen.class,Joiners.equal(Queen::getAscendingDiagonalIndex),Joiners.lessThan(Queen::getId)).penalize(HardSoftScore.ONE_HARD).asConstraint("AscendingDiagonalIndex conflict");}public Constraint descendingDiagonalIndexConflict(ConstraintFactory constraintFactory) {return constraintFactory.forEach(Queen.class).join(Queen.class,Joiners.equal(Queen::getDescendingDiagonalIndex),Joiners.lessThan(Queen::getId)).penalize(HardSoftScore.ONE_HARD).asConstraint("DescendingDiagonalIndex conflict");}
}

应用

public class NQueenApp {public static void main(String[] args) {SolverFactory<NQueen> solverFactory = SolverFactory.create(new SolverConfig().withSolutionClass(NQueen.class).withEntityClasses(Queen.class).withConstraintProviderClass(NQueenConstraintProvider.class).withTerminationSpentLimit(Duration.ofSeconds(5)));NQueen problem = generateDemoData();Solver<NQueen> solver = solverFactory.buildSolver();NQueen solution = solver.solve(problem);printTimetable(solution);}public static NQueen generateDemoData() {List<Column> columnList = new ArrayList<>();List<Row> rowList = new ArrayList<>();List<Queen> queenList = new ArrayList<>();for (int i = 0; i < 8; i++) {columnList.add(new Column(i));rowList.add(new Row(i));queenList.add(new Queen(i, null, null));}return new NQueen(columnList, rowList, queenList, null);}private static void printTimetable(NQueen nQueen) {System.out.println("");List<Column> columnList = nQueen.getColumnList();List<Row> rowList = nQueen.getRowList();List<Queen> queenList = nQueen.getQueenList();Map<Column, Map<Row, List<Queen>>> queenMap = queenList.stream().filter(queen -> queen.getColumn() != null && queen.getRow() != null).collect(Collectors.groupingBy(Queen::getColumn, Collectors.groupingBy(Queen::getRow)));System.out.println("|     | " + columnList.stream().map(room -> String.format("%-3s", room.getIndex())).collect(Collectors.joining(" | ")) + " |");System.out.println("|" + "-----|".repeat(columnList.size() + 1));for (Column column : columnList) {List<List<Queen>> cellList = rowList.stream().map(row -> {Map<Row, List<Queen>> byRowMap = queenMap.get(column);if (byRowMap == null) {return Collections.<Queen>emptyList();}List<Queen> cellQueenList = byRowMap.get(row);if (cellQueenList == null) {return Collections.<Queen>emptyList();}return cellQueenList;}).collect(Collectors.toList());System.out.println("| " + String.format("%-3s", column.getIndex()) + " | "+ cellList.stream().map(cellQueenList -> String.format("%-3s",cellQueenList.stream().map(queen -> queen.getId().toString()).collect(Collectors.joining(", ")))).collect(Collectors.joining(" | "))+ " |");System.out.println("|" + "-----|".repeat(columnList.size() + 1));}List<Queen> unassignedQueens = queenList.stream().filter(Queen -> Queen.getColumn() == null || Queen.getRow() == null).collect(Collectors.toList());if (!unassignedQueens.isEmpty()) {System.out.println("");System.out.println("Unassigned Queens");for (Queen Queen : unassignedQueens) {System.out.println("  " + Queen.getColumn() + " - " + Queen.getRow());}}}
}