题目

---

给定一棵二叉树，判断其是否是自身的镜像（即：是否对称）

例如：
下面这棵二叉树是对称的

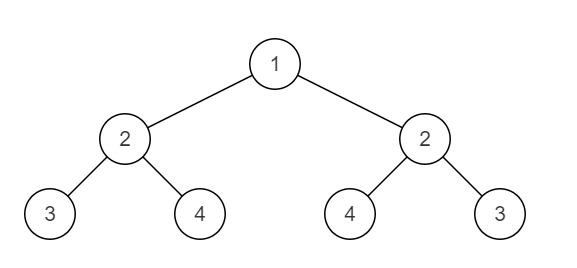
下面这棵二叉树不对称。

数据范围：节点数满足 0≤n≤1000，节点上的值满足 ∣val∣≤1000

要求：空间复杂度 O(n)，时间复杂度 O(n)

参数说明：二叉树类，二叉树序列化是通过按层遍历,#代表这这个节点为空节点，举个例子：

  1/ \
2   3/4

以上二叉树会被序列化为 {1,2,3,#,#,4}

示例1

输入：
{1,2,2,3,4,4,3}
返回值：
true

示例2

输入：
{8,6,9,5,7,7,5}
返回值：
false

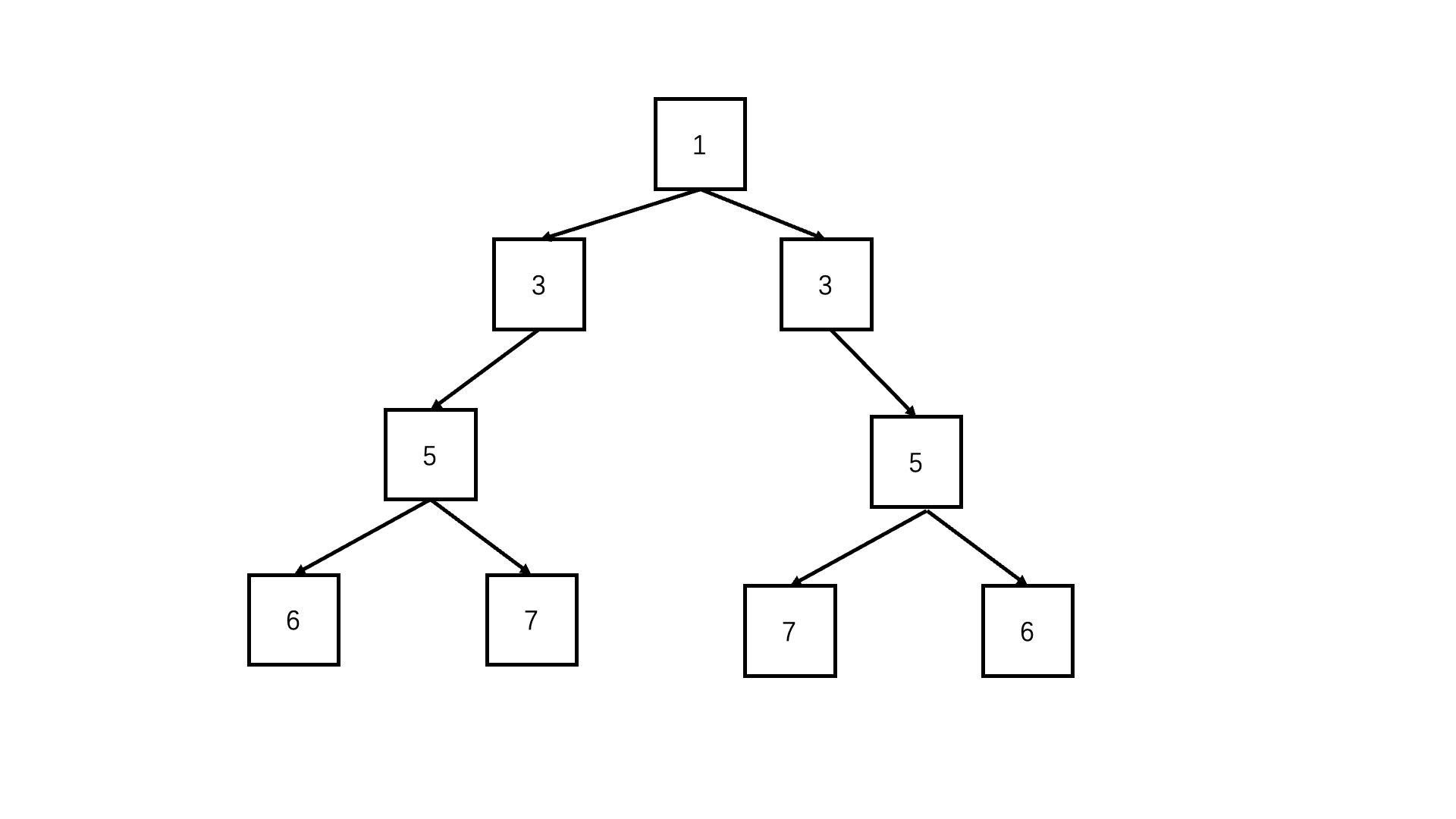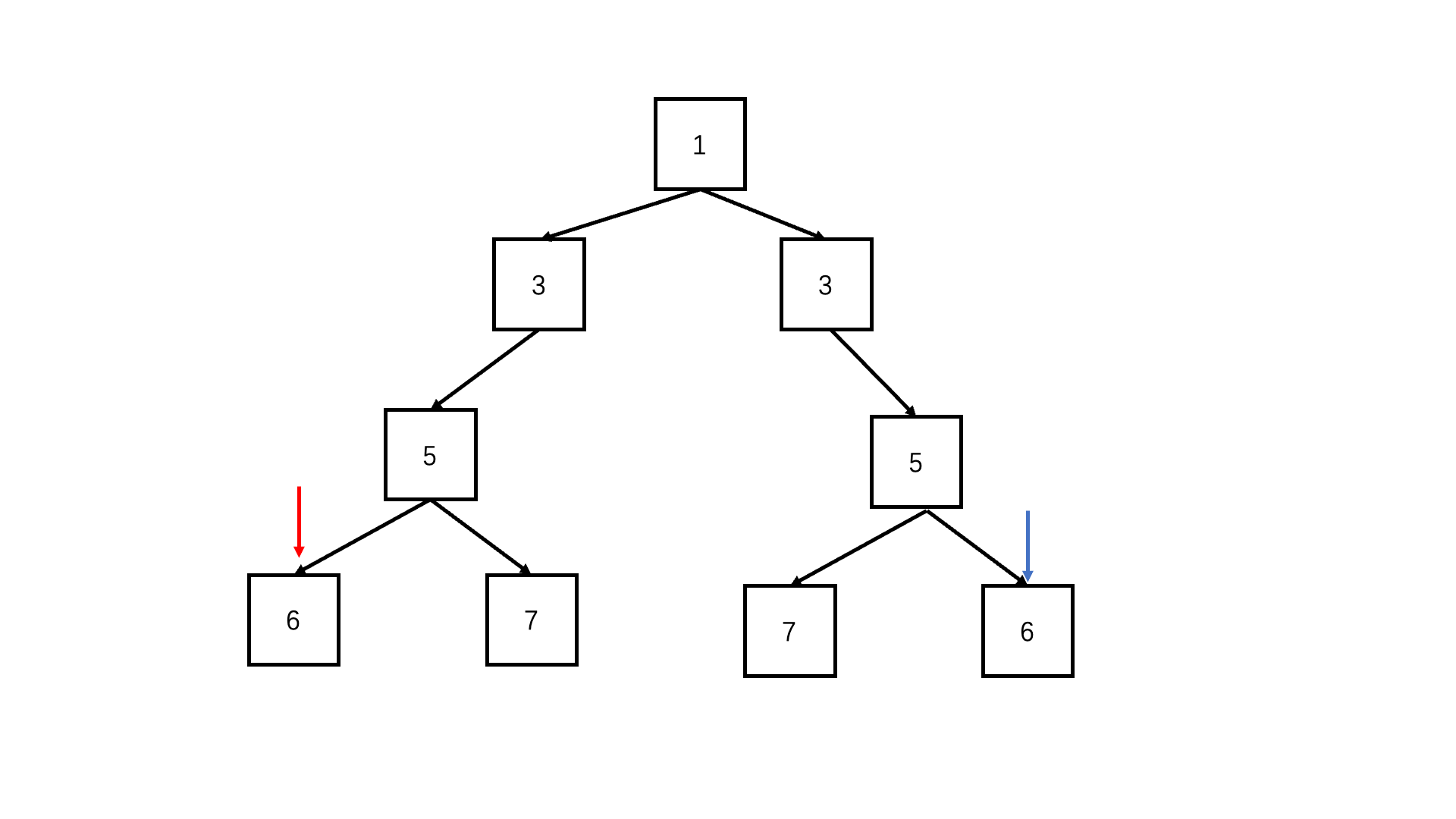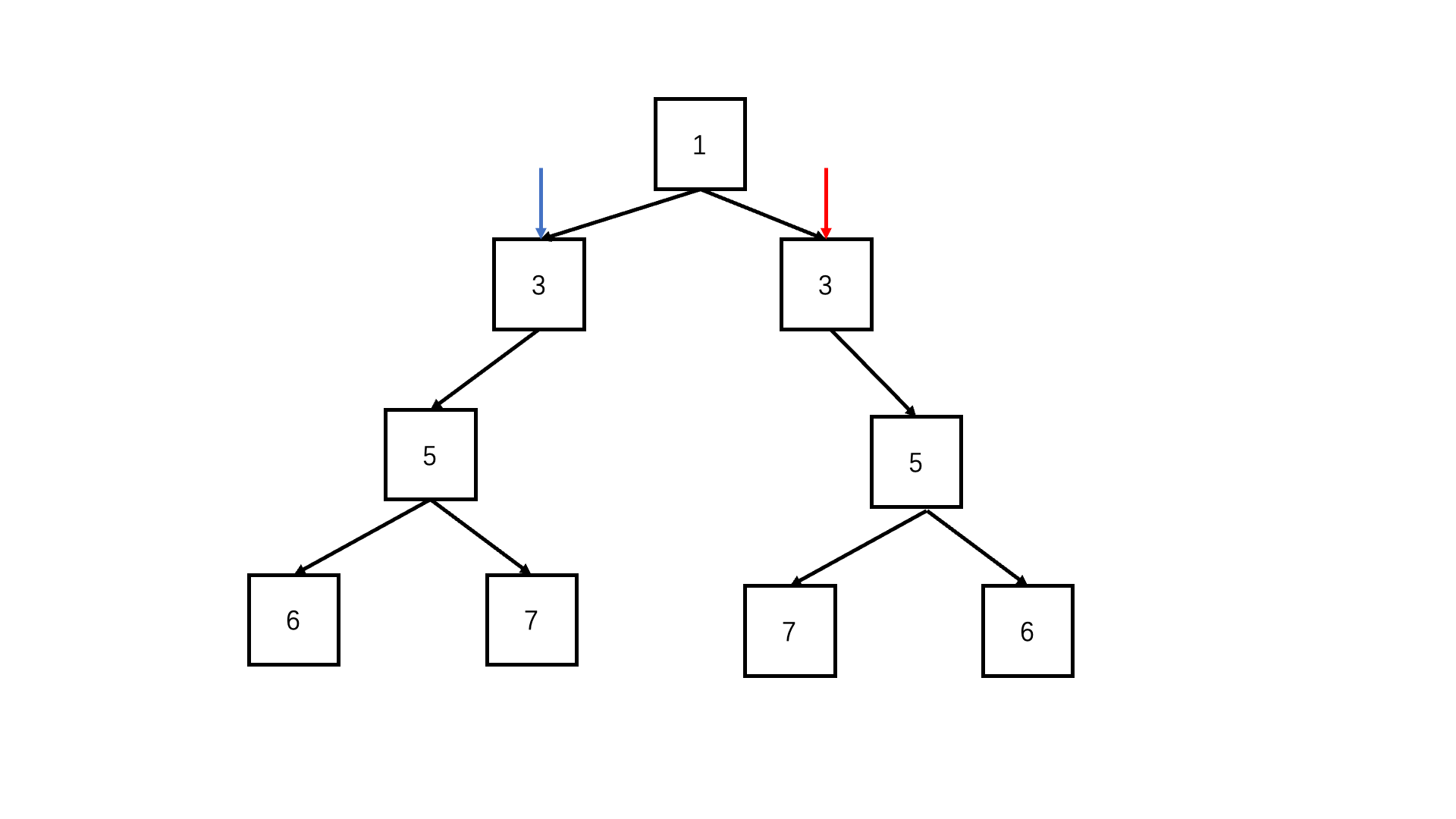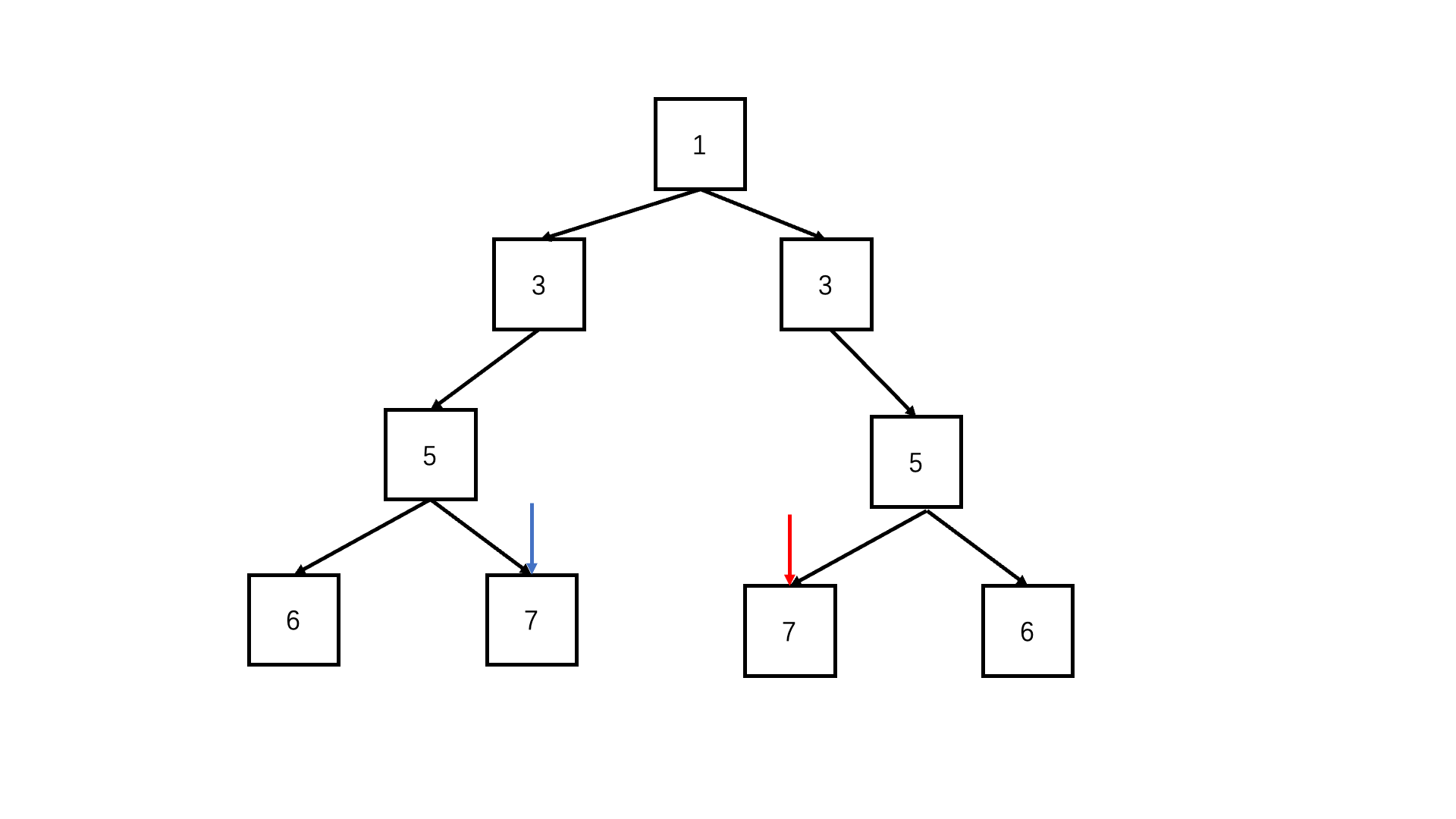
思路1

---

前序遍历递归：

• 终止条件： 当进入子问题的两个节点都为空，说明都到了叶子节点，且是同步的，因此结束本次子问题，返回true；当进入子问题的两个节点只有一个为空，或是元素值不相等，说明这里的对称不匹配，同样结束本次子问题，返回false。
• 递归： 每次同步递归比较节点一的左子树和节点二的右子树，以及节点一的右子树和节点二的左子树。

解答代码1

---

/*** struct TreeNode {*  int val;*  struct TreeNode *left;*  struct TreeNode *right;*  TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}* };*/
class Solution {public:/*** @param pRoot TreeNode类* @return bool布尔型*/bool isSymmetrical(TreeNode* pRoot) {// write code hereif (pRoot == nullptr) {return true;}return isSymmetricalByRecursion(pRoot->left, pRoot->right);}bool isSymmetricalByRecursion(TreeNode* r1, TreeNode* r2) {// 终止条件:到叶子结点返回trueif (r1 == nullptr && r2 == nullptr) {return true;}// 终止条件:节点值不等，或有一个节点为空，返回falseif (r1->val != r2->val || r1 == nullptr || r2 == nullptr) {return false;}// 本层任务return isSymmetricalByRecursion(r1->left, r2->right) && isSymmetricalByRecursion(r1->right, r2->left);}
};

思路2

---

通过bfs（广度优先）分别遍历根节点的左右子树，检查其对称性。从左往右遍历左子树，从右往左遍历右子树。

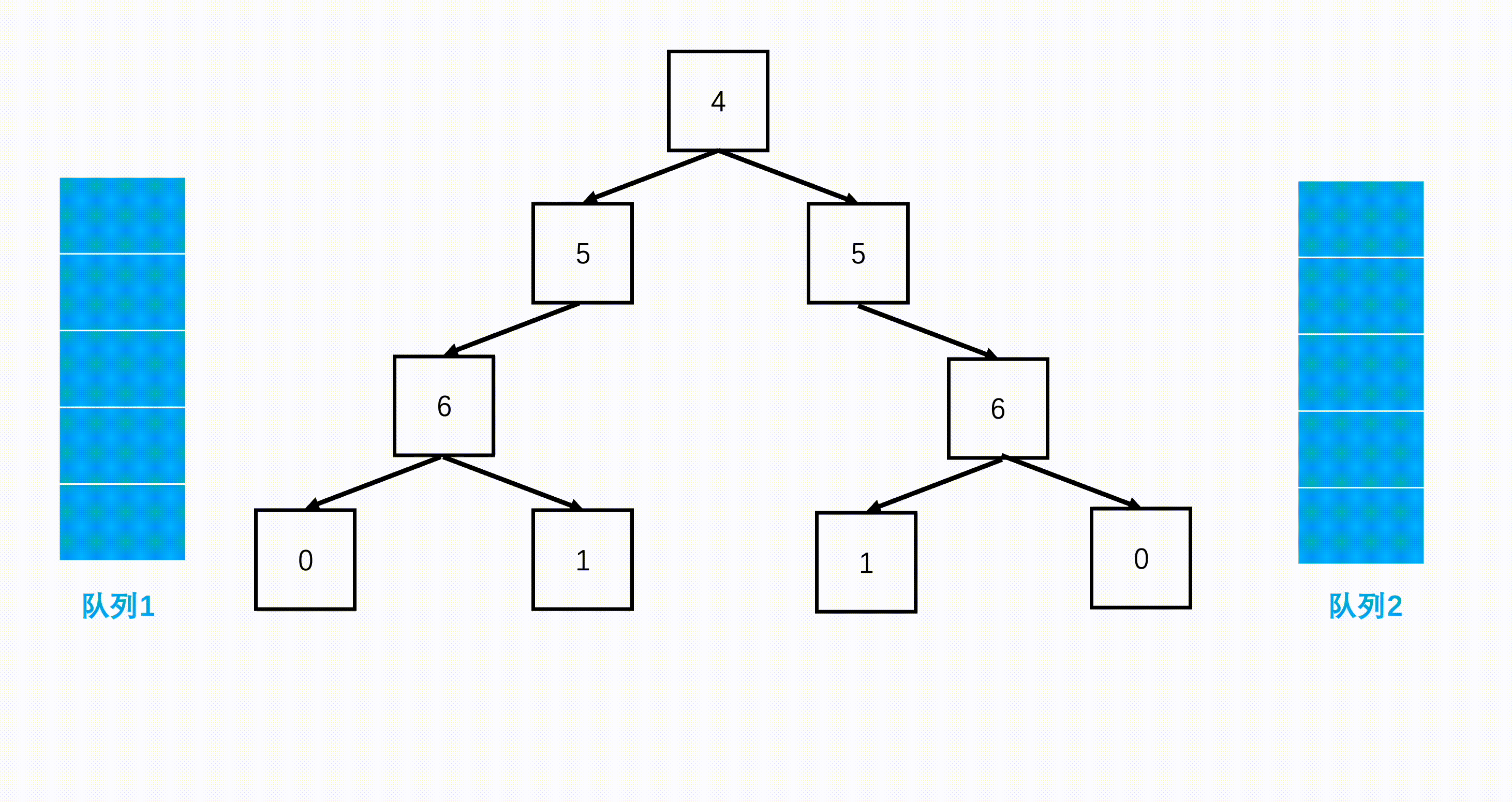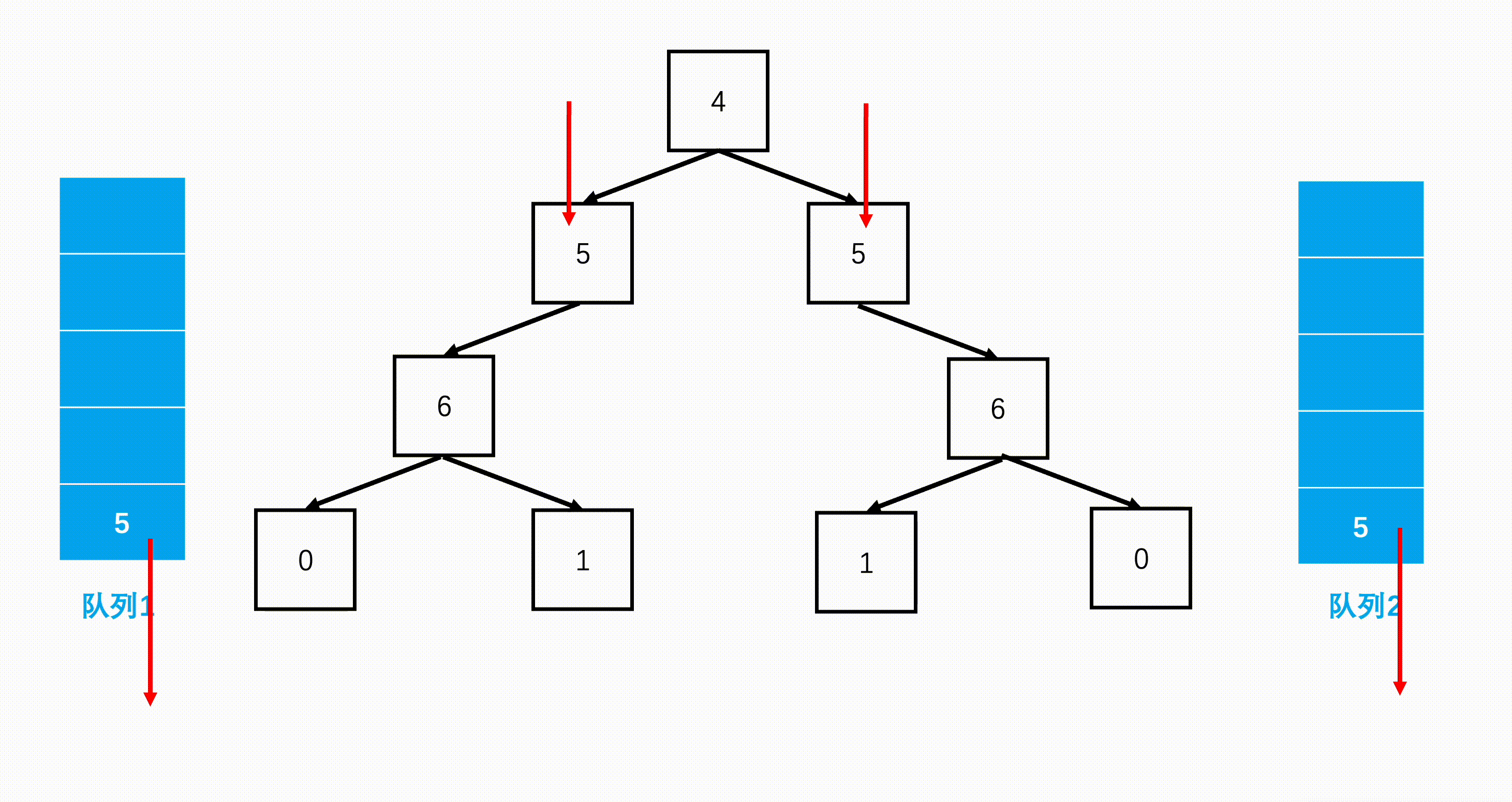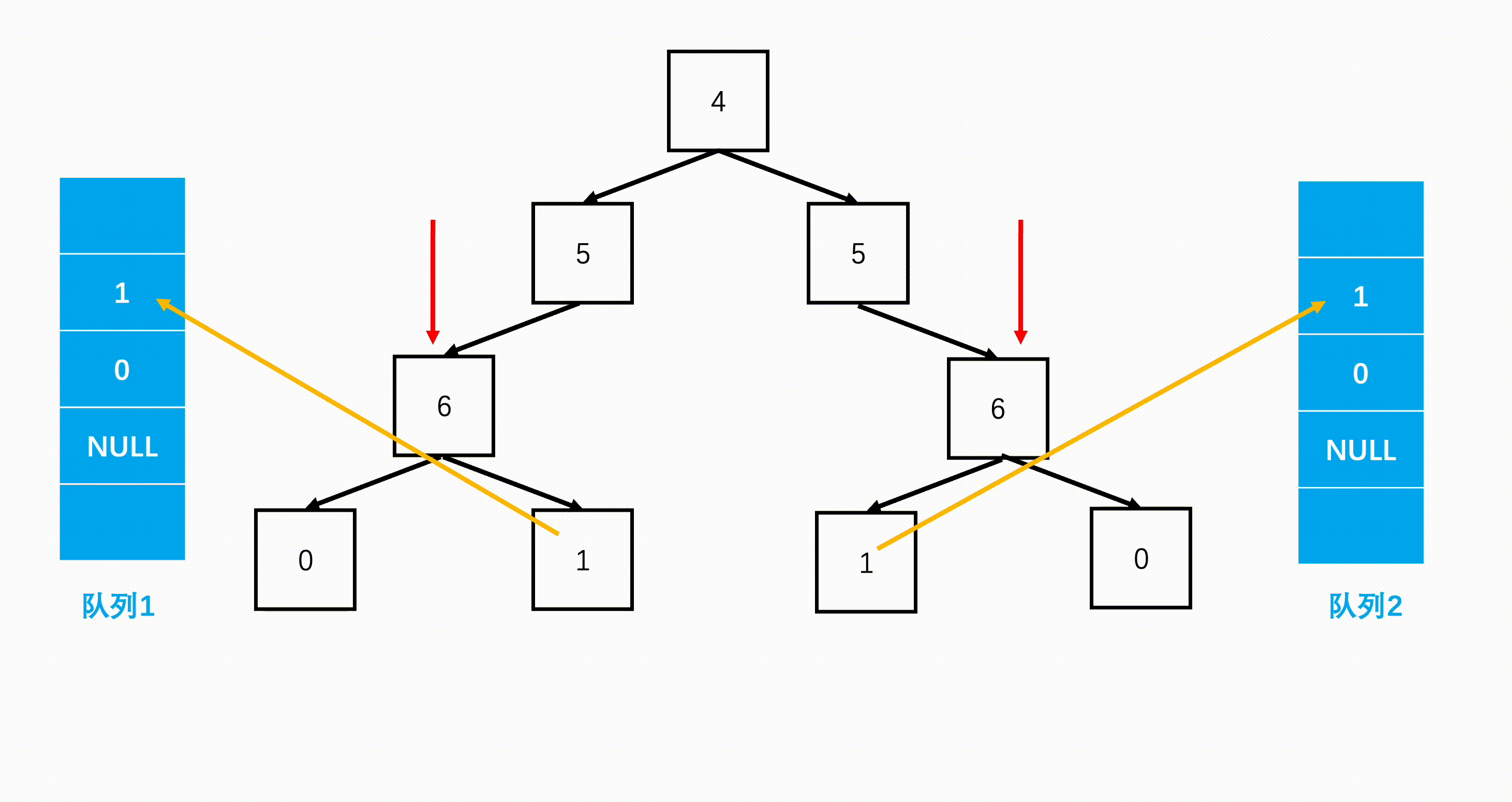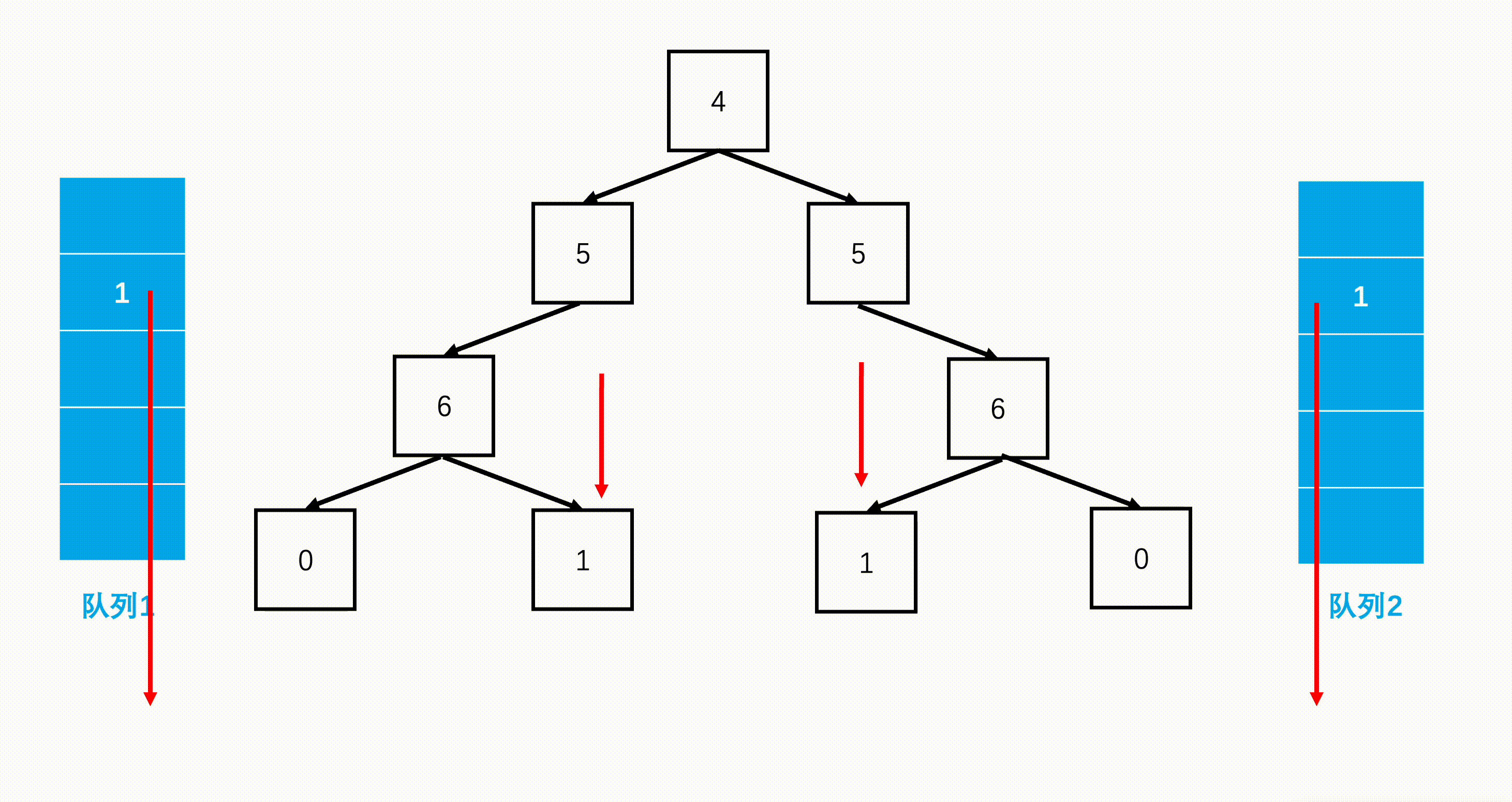
解答代码2

---

/*** struct TreeNode {*  int val;*  struct TreeNode *left;*  struct TreeNode *right;*  TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}* };*/
#include <queue>
class Solution {public:/*** @param pRoot TreeNode类* @return bool布尔型*/bool isSymmetrical(TreeNode* pRoot) {// write code hereif (pRoot == nullptr) {return true;}// bfs辅助队列queue<TreeNode*> left;queue<TreeNode*> right;left.emplace(pRoot->left);right.emplace(pRoot->right);while (!left.empty() && !right.empty()) {auto r1 = left.front();left.pop();auto r2 = right.front();right.pop();if (r1 == nullptr && r2 == nullptr) {// 两个节点都为空，则进行下一轮检测continue;}if (r1->val != r2->val || r1 == nullptr || r2 == nullptr) {return false;}// 左队列从左往右加入子节点，右队列从右往左加入子节点left.emplace(r1->left);left.emplace(r1->right);right.emplace(r2->right);right.emplace(r2->left);}return true;}
};