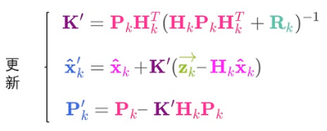什么是梯度
梯度是微积分中一个很重要的概念,在单变量的函数中,梯度其实就是函数的微分,代表着函数在某个给定点的切线的斜率;在多变量函数中,梯度是一个向量,向量有方向,梯度的方向就指出了函数在给定点的上升最快的方向;在微积分里面,对多元函数的参数求∂偏导数,把求得的各个参数的偏导数以向量的形式写出来,就是梯度
梯度下降的
梯度下降法的推导流程
- 梯度的方向是函数在给定点上升最快的方向,那么梯度的反方向就是函数在给定点下降最快的方向,以线性回归为例:

- 确认优化模型的假设函数和损失函数
参数初始化
梯度计算
更新参数
Xi
H2O CO2
益达TM
模型的训练目标即是寻找合适的 w 与 b 以最小化代价函数值。假设 w 与 b 都是一维实数,那么可以得到如下的 J 关于 w 与 b 的图