1.堆的概念
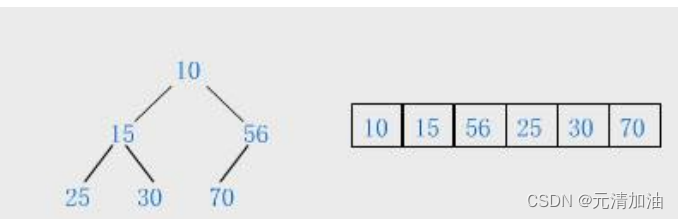
如果有一个关键码的集合 K = { k1 ,k2 ,k3 ,…,kn },把它的所有元素按完全二叉树的顺序存储方式存储在一个一维数组中,并且 k(i) < k(i*2+1) 和 k(i) < k(i*2+2), i = 0 , 1 , 2…,则称为小堆 ( 或大堆 ) 。将根节点最大的堆叫做最大堆或大根堆,根节点最小的堆叫做最小堆或小根堆。
1.1堆的性质
堆中某个节点的值总是不大于或不小于其父节点的值;堆总是一棵完全二叉树。
1.2堆的存储结构
2.堆的实现
堆的构建堆的销毁堆的插入堆的删除取堆顶的数据堆的数据个数堆的判空
2.1堆的构造与销毁
void HeapInit(HP* php) {assert(php);php->a = NULL;php->size = 0;php->capacity = 0; }void HeapDestroy(HP* php) {assert(php);free(php->a);php->a = NULL;php->size = 0;php->capacity = 0; }
2.2堆的向上与向下调整
void swap(DataType*str1, DataType*str2) {DataType temp = *str1;*str1 = *str2;*str2 = temp; } //向上调整(前提是上面是一个堆) void AdjustUp(DataType* a, int child) {//利用孩子找父亲,并且比较int parent = (child - 1) / 2;while (child > 0){// "<" 和 ">"取决与建立大小堆if (a[child] < a[parent]){swap(&a[child], &a[parent]);child = parent;parent = (child - 1) / 2;}else{break;}} } //向下调整(前提是下面左右子树是一个堆) void AdjustDown(int* a, int n, int parent)//n是数量 {//利用父亲找儿子并比较大小int child = parent * 2 + 1;while (child < n){//child + 1 < n可能没有右孩子,防止越界风险if (child + 1 < n && a[child + 1] < a[child]){child++;}// "<" 和 ">"取决与建立大小堆if (a[child] > a[parent]){swap(&a[child], &a[parent]);parent = child;int child = parent * 2 + 1;}elsebreak;} }
2.3 堆的插入与堆的删除
//先插入一个数到数组的尾上,再进行向上调整算法,直到满足堆 void HeapPush(HP* php, DataType x) {assert(php);//判断是否要扩容if (php->size == php->capacity){int newCapacity = php->capacity == 0 ? 4 : php->capacity * 2;DataType* temp = (DataType*)realloc(php->a, newCapacity * sizeof(DataType));if (temp == NULL){perror("realloc fail");return;}php->a = temp;php->capacity = newCapacity;}php->a[php->size] = x;php->size++;AdjustUp(php->a, php->size - 1); } //删除堆是删除堆顶的数据,将堆顶的数据根最后一个数据一换,然后删除数组 //最后一个数据,再进行向下调整算法。 void HeapPop(HP* php) {assert(php);swap(&php->a[0], &php->a[php->size - 1]);php->size--;AdjustDown(php->a, php->size, 0); }
2.4堆的数据个数与堆的判空和取得堆的堆顶元素
DataType HeapTop(HP* php) {assert(php);assert(!HeapEmpty(php));return php->a[0]; } bool HeapEmpty(HP* php) {assert(php);return php->size == 0; }int HeapSize(HP* php) {assert(php);return php->size; }