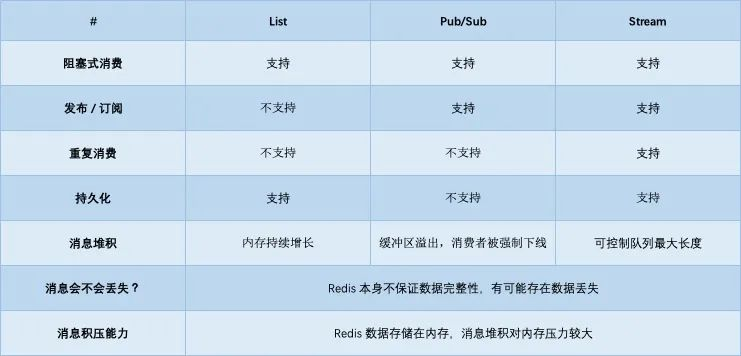
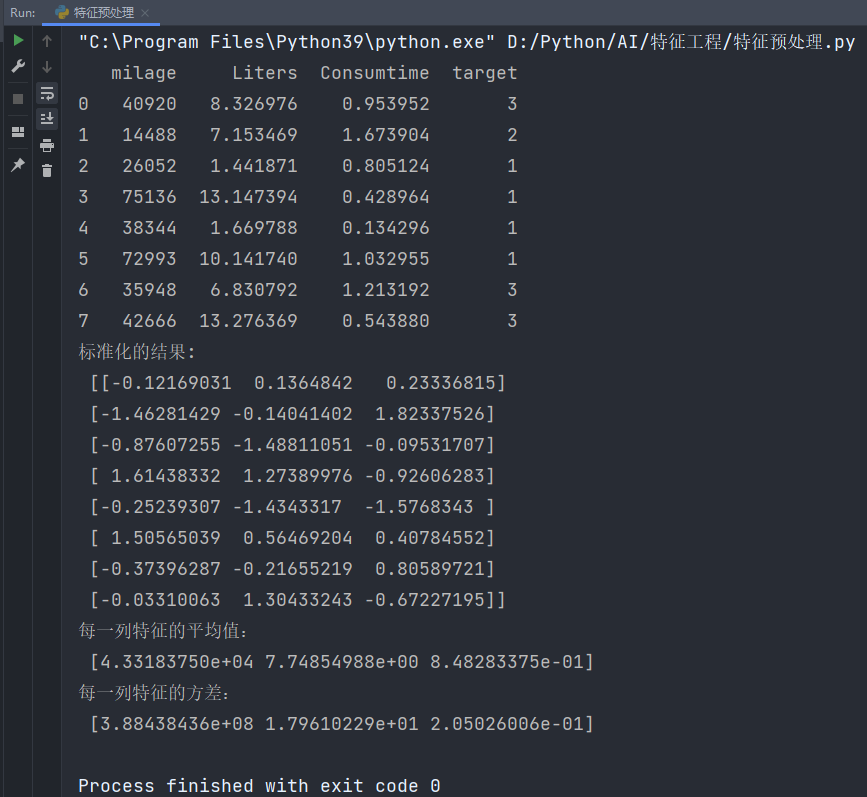
在开展统计分析的过程中,分类变量(定序和定类变量)是我们研究的一个重点。通常我们分析分类变量间关系时,最常用的分析方法是卡方检验,其次是逻辑回归和对数线性模型等。
如果类别变量的分类较少,我们可以通过卡方检验判断行变量和列变量间是否相互独立,同时还可以通过查看列联表或进行进行事后两两比较,判断各变量的不同组别间具体存在怎样的差异

但如果涉及的分类变量较多时,卡方检验能给的信息就很有限了,它并不能告诉我们两个变量之间具体存在怎样的联系。而逻辑回归方法和对数线性模型等方法的操作和解释相对比较复杂,学起来比较让人头疼。所以今天我想向大家介绍对应分析方法。
对应分析方法又称相应分析,它善于展示两个/多个分类变量各类间的关系,能够将交叉列联表的数据信息转化为二维散点图,直观、简单的描述庞杂的列联表数据中所蕴含的对应关系。
它是于1970年由法国统计学家J.P.Beozecri提出来的,起初在法国和日本最为流行,后来引入到美国,是在R型和Q型因子分析基础上发展起来的一种多元统计方法。
简单对应分析是分析某一研究事件两个分类变量间的关系,其基本思想以点的形式在较低纬的空间中表示列联表的行和列中各元素的比例结构,可以在二维空间更加直观的通过空间距离反映两个分类变量间的关系。属于分类变量的典型相关分析。
Fisher在1940采集了5387名苏格兰人的眼睛和头发颜色数据,并利用对应分析方法分析了眼睛颜色和头发之间是否存在显著关系,这是利用对应分析方法开展的经典案例。有关这个案例的分享很多,感兴趣的读者可以到网上搜索查看。
案例数据集介绍
接下来我将用SPSS中的自带数据集coffee.sav向大家介绍对应分析方法。
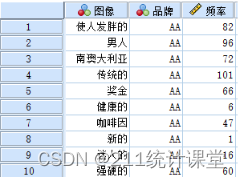
研究者收集了4662份有关6个冰咖啡品牌与23张感知图像的数据,其中6个品牌分别表示为AA、BB、CC、DD、EE和FF,23张感知图像表示的是不同的形象特征。研究者希望知道这6个冰咖啡品牌和23种感知图像之间是否存在何种联系,即不同的冰咖啡品牌是否更倾向于某种品牌形象。
打开数据集:
选择文件 -> “欢迎”对话框(SPSS25及以上版本),在欢迎对话框中选择样本文件, 选择coffee.sav,选择打开。SPSS会自动打开这份数据文件。
.

该数据集的部分数据截图如下所示:
数据分析1:个案加权
当涉及到分类变量的频数分析时,一般都需要对数据进行加权处理。(扩展阅读:加权到底是怎么回事儿?)
在本案例中,频率变量记录了不同品牌与不同图像属性相关的频数,因此我们需要对频率变量进行加权。
加权操作步骤:选择菜单数据 ->个案加权,将频率变量拖入频率变量,点击确定。对话框如下图所示:

数据分析2:卡方检验
因为对应分析不能用于相关关系的假设检验,所以在开展对应分析之间需要先对数据进行卡方检验,判断行变量和列变量之间是否独立。只有两变量之间存在显著联系,才能开展下一步的对应分析。
卡方检验操作步骤:选择菜单分析 -> 描述统计 -> 交叉表,将图像和品牌变量分别放入行列对话框;点击统计按钮,在统计复选框中勾选卡方,点击继续,点击确定。对话框如下图所示:

得到的分析结果如下:

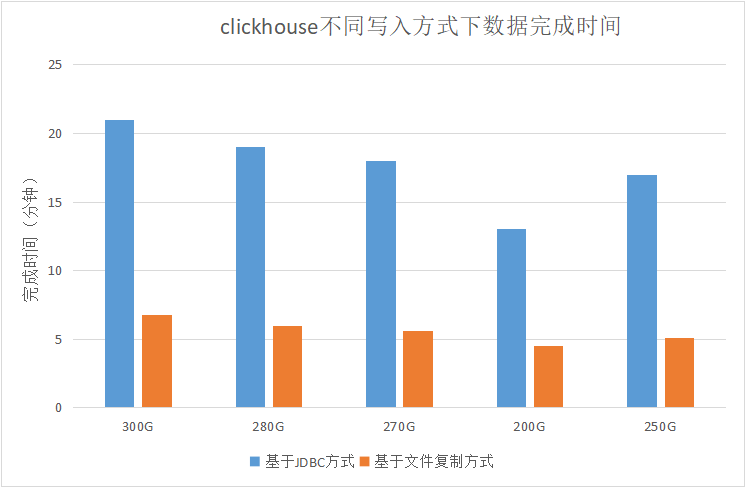
从上方的卡方检验分析表来看,卡方值为3746.968,P值=0.000(<0.05),说明图像和品牌变量之间存在显著关联。
但究竟存在怎样的关联呢?卡方检验不能给我们答案,接下来,我们需要采用更复杂的对应分析方法才能得到进一步的分析结果。
数据分析3:对应分析
对应分析的操作步骤1:
选择菜单分析 -> 降维 -> 对应分析,将图像和品牌变量分别选入行和列;

对应分析的操作步骤2:
在相应的行和列下面定义范围,根据选取的变量分别填入最小值和最大值;其中图像变量的定义范围是1~23,品牌变量的定义范围是1~6;
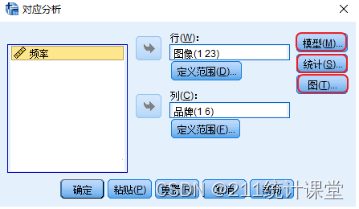
对应分析的操作步骤3:
点击模型按钮,进入模型复选框;对话框如下图所示:
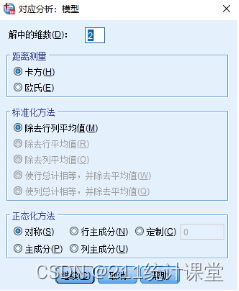
解的维数:相当于因子分析和主成分分析中的维数,通常默认为2,也可以根据累计方差(一般大于85%即可)来选择;
距离度量:像本案例中的分类变量一般都选择“卡方”,而数值变量则选择“欧式距离”;
标准化方法:选择“除去行列平均值“;
标准化方法:
a:除去行列平均值:行和列均中心标准化;
b:除去行平均值:对行中心标准化;
c:除去列平均值:对列中心标准化;
d:使行总计相等,并除去平均值:使行的边际相等,对行中心化;
e:使列总计相等,并除去平均值:使列的边际相等,对列中心化;
正态化方法:选择默认值“对称”;
正态化方法:
a:对称法:适用于行列变量间有相关关系;
b:行(列)主成分:适用于行(列)变量间有一定的差别;
c:主成分法:既考虑行,也考虑到列;
对应分析的操作步骤4:
点击统计按钮,进入统计复选框,勾选前3个选项即可:

统计量:
a:对应表:生成行列对应表; b:行点概述:行变量的因子分析表; c:列点概述:列变量的因子分析表;d:对应表的排列:研究一定维数的对应表(此处的维数应小于对应表中的最大维数);e:行概要:行变量的频数分布表; f:列概要:列变量的频数分布表; g:置信统计量:显示在95%置信区间下的统计量。
对应分析的操作步骤5:
点击图按钮,进入图形复选框,选择如下默认选项即可:

图形复选框:
a:双标图(必选):可以在双坐标轴上,同时展示行列变量在坐标系中的距离关系; b:行(列)点:行(列)变量的散点图; c:标识标签宽度:为≤20的整数; d:折线图(通常不选):已转换的行(列)类别是指由行(列)的因子构成的折线图;e:图维数直接选择默认选项“显示解中的所有的维”即可; f:限制维数:最低维数通常设定为1,最高维数设定为总体样本量-1;
上述5步均设置完成后,点击继续,点击确定,即可得到对应分析结果,其中主要包括6个图表。
分析结果解析
(1)信用表
对应分析结果中首先会输出该模块的版权信息,说明该模块是由荷兰的了Leiden大学Leiden SPSS课题组编制的。这部分信息与我们的分析结果无关,可以忽略。
(2)交叉列联表
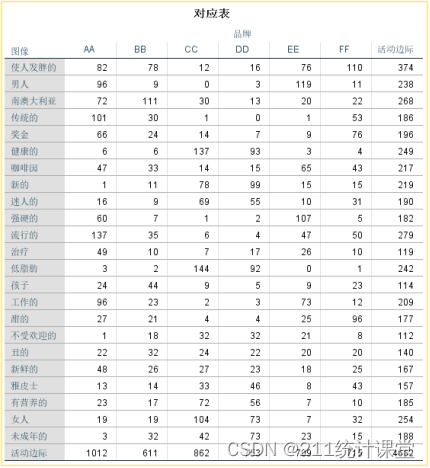
上表是图像变量和品牌变量组成的交叉列联表,交叉单元格内的数值代表频数,在之前的卡方检验环节也有输出。
对应分析后续的计算完全是基于该交叉列联表展开,所以它在分析环节十分重要。
不过这个列联表呈现的数字信息较多,阅读效果并不直观,我们没有必要对它花太多时间,稍加浏览无异常值即可。

上表是对应分析的结果汇总表。在对应分析中,最多可提取的维数等于两变量最小类别数-1。但往往前2~3个维度就携带了绝大多数的信息,因此可以只对前几个维度进行观察。
在本案例中,变量的最小类别数是6,所以摘要表中提取了5个维数。前3个维数的累积携带了91.3%的原始信息量,即已经携带了绝大部分的信息,因此我们只需要对前3个维度进行进一步考察。
最后一行显示的是上方交叉列联表的卡方检验结果,这部分与我们之前单独开展的卡方检验结果一样,说明品牌变量和图像变量之间存在显著关联,使对应分析结果有实际意义。
(4)行(列)点总览


上面的两个表是行变量和列变量各类别的分析结果概况,由于各类别均以散点的形式在空间中呈现,故称行/列点总览。表中主要给出各类别在各维度上的评分,以及相应的贡献量两大类信息。
以上面的“列点总览表”为例:
“数量”实际上就是指各类别的构成比,如:品牌AA占总数的构成比是21.7%,以此类推。构成比越高,说明越不易受个别极端样本值的影响。
“维得分”给出了各类别在相关维度上的评分,如:品牌AA在二维空间中的坐标值是(-0.782,-0.073),依次类推,根据坐标值能得到最终的对应分析散点图。
然后给出“惯量”在列变量中的分解情况,它反映了总惯量(0.804)中分别由各列变量类别提供的部分,数值越大,说明该类别对惯量的贡献越大,此处贡献最大的是品牌CC。
“贡献”给出在各维度上信息量在各类别间的分解情况。“点对维的惯量”表示分类变量中每个类别对维度的贡献,如:本例中可见第1维度的信息主要被CC、DD这2个品牌所携带,说明这2个类别在第1维度上表现较好;第2维度的信息主要被EE、FF这2个品牌所携带,说明这2个类别在第2维度上表现较好。
“维对点的惯量”正好相反,表示每个类别信息分别在两个维度的比例,例如品牌AA的信息在第1个维度中占74.4%,在第2个维度只有0.4%。
(5)对应分析散点图
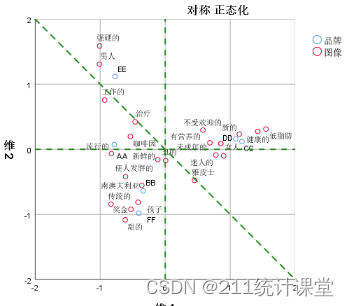
在上图的对应分析散点图中,分别向X轴和Y轴加入参考线,两条参考线相交于原点(0,0),原点表示没有任何倾向,没有任何关联的一个中心位置。
散点图显示“新鲜的”和“丑的”都非常接近原点;在散点图的左上角,“强悍”、“男人”、“工作的”靠得较近;左下角是“甜的”、“肥的”、“孩子”、“优质的”靠得较近;“健康”、“低脂”、“营养”、“新的”集中在散点图的右侧。
左上角的品牌EE所展示的品牌联想多与男性、强硬,工作相关;AA品牌是最受欢迎的,也被认为是咖啡因含量最高的;BB和FF品牌让人更多的联想到“甜的”、“优质的”、“使人发胖的”等关键词;CC和DD品牌虽然被认为是新的和健康的,但也是最不受欢迎的。
同时,为了进一步的解释,我还在散点图上绘制了一条经过原点的斜45°的直线。你会发现这条线穿过了男性形象和雅皮士这两个属性,而且男性品牌的联想模式与雅皮士品牌的联想模式相互对立。也就是说,“强硬的”、“男人”最常与EE品牌相关,最少与CC品牌相关,而雅皮士最常与CC品牌相关,最少与EE品牌相关。
通过上述的对应分析散点图,我们就可以非常直观而简明的得到品牌与图像之间的关联特征。
对应分析の注意事项
- 对应分析不能用于相关关系的假设检验。它虽然可以揭示变量间的联系,但仍然只是一种统计描述方法,不能说明两个变量之间的联系是否显著,因而在做对应分析之前,可以用卡方统计量检验两个变量的是否独立。
- 对应分析输出的图形通常是二维的,这是一种降维的方法,将原始的高维数据按一定规则投影到二维图形上。而投影可能引起部分信息的丢失。
- 对极端值敏感,应尽量避免极端值的存在。如有取值为零的数据存在时,可视情况将相邻的两个状态取值合并。对于小样本不推荐使用。
- 原始数据的无纲量化处理。运用对应分析法处理问题时,各变量应具有相同的量纲(或者均无量纲)。
- 无法自动判断最佳维度数,所需维度数需要研究者根据专业知识自行决定。