😶‍🌫️Take your time ! 😶‍🌫️
💥个人主页：🔥🔥🔥大魔王🔥🔥🔥
💥代码仓库：🔥🔥魔王修炼之路🔥🔥
💥所属专栏：🔥魔王的修炼之路–数据结构🔥
如果你觉得这篇文章对你有帮助，请在文章结尾处留下你的点赞👍和关注💖，支持一下博主。同时记得收藏✨这篇文章，方便以后重新阅读。

---

一、前言

学习完二叉树的顺序存储（堆），那么本篇博客将讲述二叉树的链式存储（左孩子右兄弟）。

• 因为普通的二叉树增删查改没有任何意义，总不能只是因为结构复杂就用这个没有任何意义的普通二叉树来存储数据，所以我们不进行它的增删查改学习，而是先了解了解普通二叉树的一些操作：求二叉树节点个数、深度等等。

下面的所有内容都是以下图二叉树举例

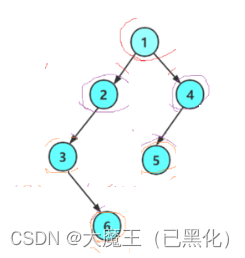
二、二叉树的遍历

前中后序

前序：根左右
中序：左根右
后序：左右根

#include <stdio.h>
#include <stdlib.h>
#include <assert.h>typedef struct BTNode
{struct BTNode* left;struct BTNode* right;int data;
}BTNode;BTNode* BuyNewnode(int x)
{BTNode* newnode = (BTNode*)malloc(sizeof(BTNode));if (newnode == NULL){perror("malloc error");assert(newnode);}newnode->data = x;newnode->left = NULL;newnode->right = NULL;return newnode;
}BTNode* BTCreat()
{BTNode* node1 = BuyNewnode(1);BTNode* node2 = BuyNewnode(2);BTNode* node3 = BuyNewnode(4);BTNode* node4 = BuyNewnode(3);BTNode* node5 = BuyNewnode(5);BTNode* node6 = BuyNewnode(6);node1->left = node2;node1->right = node3;node2->left = node4;node3->left = node5;node4->right = node6;return node1;
}//前序
void PreOrder(BTNode* n1)
{if (n1 == NULL){printf("NULL ");return;}printf("%d ", n1->data);PreOrder(n1->left);PreOrder(n1->right);
}//中序
void InOrder(BTNode* n1)
{if (n1 == NULL){printf("NULL ");return;}InOrder(n1->left);printf("%d ", n1->data);InOrder(n1->right);
}//后序
void PostOrder(BTNode* n1)
{if (n1 == NULL){printf("NULL ");return;}PostOrder(n1->left);PostOrder(n1->right);printf("%d ", n1->data);
}int main()
{BTNode* n1 = BTCreat();//前序PreOrder(n1);printf("\n");//中序InOrder(n1);printf("\n");//后序PostOrder(n1);printf("\n");return 0;
}

三、求二叉树结点个数

递归、分治，每层只需要知道自己下一层节点的总个数即可，然后传给上一层。记得每层向上回归的时候要加上自己的那一个。

#include <stdio.h>
#include <stdlib.h>
#include <assert.h>typedef struct BTNode
{struct BTNode* left;struct BTNode* right;int data;
}BTNode;BTNode* BuyNewnode(int x)
{BTNode* newnode = (BTNode*)malloc(sizeof(BTNode));if (newnode == NULL){perror("malloc error");assert(newnode);}newnode->data = x;newnode->left = NULL;newnode->right = NULL;return newnode;
}BTNode* BTCreat()
{BTNode* node1 = BuyNewnode(1);BTNode* node2 = BuyNewnode(2);BTNode* node3 = BuyNewnode(4);BTNode* node4 = BuyNewnode(3);BTNode* node5 = BuyNewnode(5);BTNode* node6 = BuyNewnode(6);node1->left = node2;node1->right = node3;node2->left = node4;node3->left = node5;node4->right = node6;return node1;
}int BTSize(BTNode* n1)
{if (n1 == NULL)return 0;return BTSize(n1->left) + BTSize(n1->right) + 1;
}int main()
{BTNode* n1 = BTCreat();//二叉树节点个数int size = BTSize(n1);printf("%d\n", size);return 0;
}

四、求二叉树深度

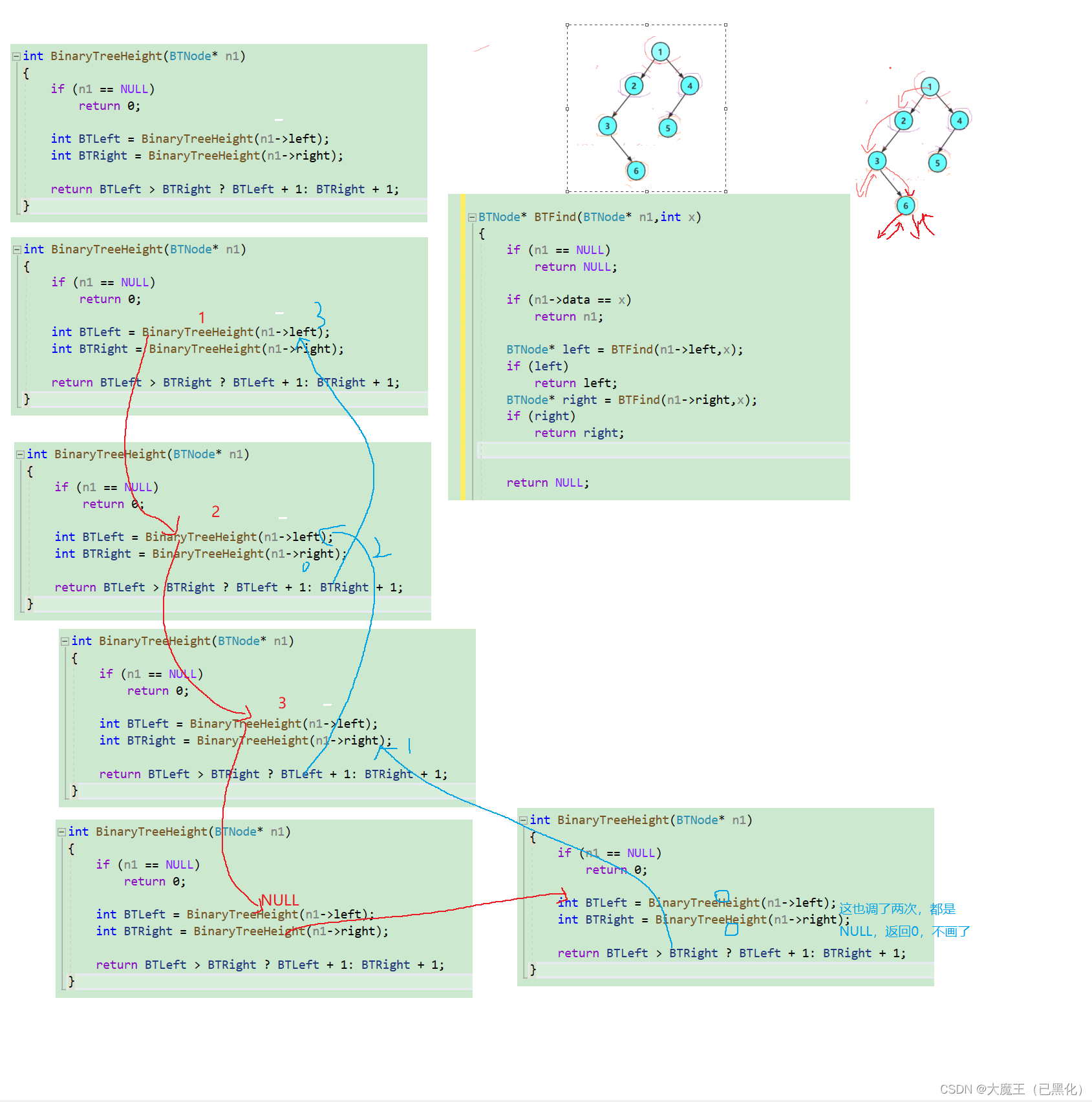
还是递归和分治，每层只需要直到自己左子树和右子树中最高的那个即可。

#include <stdio.h>
#include <stdlib.h>
#include <assert.h>typedef struct BTNode
{struct BTNode* left;struct BTNode* right;int data;
}BTNode;BTNode* BuyNewnode(int x)
{BTNode* newnode = (BTNode*)malloc(sizeof(BTNode));if (newnode == NULL){perror("malloc error");assert(newnode);}newnode->data = x;newnode->left = NULL;newnode->right = NULL;return newnode;
}BTNode* BTCreat()
{BTNode* node1 = BuyNewnode(1);BTNode* node2 = BuyNewnode(2);BTNode* node3 = BuyNewnode(4);BTNode* node4 = BuyNewnode(3);BTNode* node5 = BuyNewnode(5);BTNode* node6 = BuyNewnode(6);node1->left = node2;node1->right = node3;node2->left = node4;node3->left = node5;node4->right = node6;return node1;
}
int BinaryTreeHeight(BTNode* n1)
{if (n1 == NULL)return 0;int BTLeft = BinaryTreeHeight(n1->left);int BTRight = BinaryTreeHeight(n1->right);return BTLeft > BTRight ? BTLeft + 1: BTRight + 1;
}
int main()
{BTNode* n1 = BTCreat();//二叉树深度int BTHeight = BinaryTreeHeight(n1);printf("%d\n", BTHeight);return 0;
}

五、第k层节点个数

举例来说：第三层是相对于第一层来说的，相对于第二层就是第二层，相对于第三层就是第一层，也就是本层。

#include <stdio.h>
#include <stdlib.h>
#include <assert.h>typedef struct BTNode
{struct BTNode* left;struct BTNode* right;int data;
}BTNode;BTNode* BuyNewnode(int x)
{BTNode* newnode = (BTNode*)malloc(sizeof(BTNode));if (newnode == NULL){perror("malloc error");assert(newnode);}newnode->data = x;newnode->left = NULL;newnode->right = NULL;return newnode;
}BTNode* BTCreat()
{BTNode* node1 = BuyNewnode(1);BTNode* node2 = BuyNewnode(2);BTNode* node3 = BuyNewnode(4);BTNode* node4 = BuyNewnode(3);BTNode* node5 = BuyNewnode(5);BTNode* node6 = BuyNewnode(6);node1->left = node2;node1->right = node3;node2->left = node4;node3->left = node5;node4->right = node6;return node1;
}
int BTKLevel(BTNode* n1,int k)
{if (n1 == NULL)return 0;if (k == 1)return 1;return BTKLevel(n1->left,k-1) + BTKLevel(n1->right,k-1);
}
int main()
{BTNode* n1 = BTCreat();//第K层有几个节点int k = BTKLevel(n1,4);printf("%d\n", k);return 0;
}

六、返回某个节点的地址

首先看能否找到该节点，找到的话返回该节点的地址，找不到的话返回NULL。

#include <stdio.h>
#include <stdlib.h>
#include <assert.h>typedef struct BTNode
{struct BTNode* left;struct BTNode* right;int data;
}BTNode;BTNode* BuyNewnode(int x)
{BTNode* newnode = (BTNode*)malloc(sizeof(BTNode));if (newnode == NULL){perror("malloc error");assert(newnode);}newnode->data = x;newnode->left = NULL;newnode->right = NULL;return newnode;
}BTNode* BTCreat()
{BTNode* node1 = BuyNewnode(1);BTNode* node2 = BuyNewnode(2);BTNode* node3 = BuyNewnode(4);BTNode* node4 = BuyNewnode(3);BTNode* node5 = BuyNewnode(5);BTNode* node6 = BuyNewnode(6);node1->left = node2;node1->right = node3;node2->left = node4;node3->left = node5;node4->right = node6;return node1;
}
BTNode* BTFind(BTNode* n1,int x)
{if (n1 == NULL)return NULL;if (n1->data == x)return n1;BTNode* left = BTFind(n1->left,x);if (left)return left;BTNode* right = BTFind(n1->right,x);if (right)return right;return NULL;}
int main()
{BTNode* n1 = BTCreat();//返回某个值的位置BTNode* p = BTFind(n1,9);if(p!=NULL)printf("%p\n", p);return 0;
}

七、总结

• 博主长期更新，博主的目标是不断提升阅读体验和内容质量，如果你喜欢博主的文章，请点个赞或者关注博主支持一波，我会更加努力的为你呈现精彩的内容。

🌈专栏推荐
😈魔王的修炼之路–C语言
😈魔王的修炼之路–数据结构初阶
😈魔王的修炼之路–C++
😈魔王的修炼之路–Linux
更新不易，希望得到友友的三连支持一波。收藏这篇文章，意味着你将永久拥有它，无论何时何地，都可以立即找到重新阅读；关注博主，意味着无论何时何地，博主将永久和你一起学习进步，为你带来有价值的内容。