优先级队列

在优先级队列中存储的元素具有优先级，可以返回优先级较高的元素。
逻辑结构采用的是堆（完全二叉树），存储结构是用了数组（将二叉树层序遍历存储）

几点说明

1. 设父节点的下标为i，那么左孩子的下标为2i+1，右孩子的下标为2i+2

小根堆

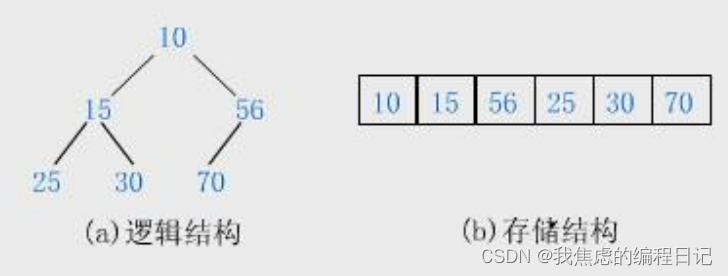
大根堆

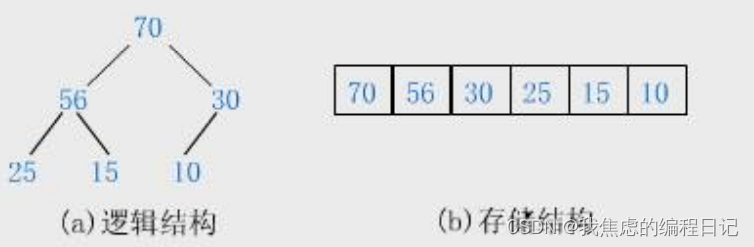
建堆算法

向下调整算法 & 初始化堆

从最后一个根节点（也就是倒数第二层）开始向上进行建堆，对每一棵子树都进行大（小）根堆的调整。

1. 从两个（一个）子树中找到比根节点大（小）的结点，然后进行交换
2. 父节点向上走（令parent = child），子节点也往上走（child = 2*parent+1）

需要注意的是：
① 不是每个结点都是有左（右）子树的，需要进行判断，防止越界
② 调整一直要进行到数组的末尾（child < array.length）

代码：

public PriorityQueue(int[] array) {this.array = new int[11];System.arraycopy(array,0,this.array,0,array.length);usedSize = array.length;// 只要根节点没有到顶，那就一直向上进行调整//（宏观向上寻找根节点，微观从每个根节点向下进行调整）for (int root = (array.length-1-1)/2; root >= 0; root--) {shiftDown(root, usedSize);}}public void shiftDown(int parent, int usedSize) {// 左孩子int child = 2 * parent + 1;// 因为是向下调整，所以找到头上的根节点后，一直向下走，// 直到不能再走(child < usedSize)while (child < usedSize) {// 如果右孩子的值更大，那就应该将child变为右孩子的下标，同时保证这个结点有右孩子if ((child + 1 < usedSize) && (array[child + 1] > array[child])) {child = 2 * parent + 2;}// 与根节点进行比较，如果孩子大，那就交换if (array[child] > array[parent]) {swap(child, parent);// 孩子和父亲都向下移动进行调整parent = child;child = 2 * parent + 1;} else {// 只要有一个结点不用调整，那就不需要继续往下走了，因为下面的之前已经调整过了break;}}

向上调整算法 & 插入

在插入的操作中，向上调整只需要进行一次，因为除了刚刚插进来的最后一个元素与其他的结点不匹配，其他的结点都已经在各自的树中形成自己的大根堆，所以只需要从最后一个结点出发向上调整，直到这个叶子结点变为新的根节点（最大的根节点或者是某一层的新根节点再不能向上走）。

public void offer(int val) {// 先判断是否已满if (isFull() == true) {// 已满，扩容array = Arrays.copyOf(array, 2*array.length);}// 插到数组的最后一个位置array[usedSize++] = val;// 使用向上调整进行重新分配int child = usedSize-1;shiftUp(child);}private void shiftUp(int child) {int parent = (child - 1) / 2;// 只要这个插入的孩子节点没到根部，// 那就一直进行调整，或者到了某一层不用调整了while (child >= 0) {if (array[child] > array[parent]) {swap(child, parent);child = parent;parent = (child - 1) / 2;} else {break;}}}

删除

删除的就是堆头元素，最大（小）元素。
具体做法：
将堆头元素与末尾元素交换位置，随后对根节点所在的树进行向下调整。

• 问：为什么只用从根节点开始进行向下调整？
• 因为在之前的初始化过程中，所有树都已经是大（小）根堆，只有刚才进行交换的过程中，改变了根节点的数据使得这棵树不为大（小）根堆，所以只需要调整这棵树。

代码：

public void poll() {// 删除最大的元素，先将堆头的元素与最后一个进行交换，然后再进行向下调整swap(0, usedSize-1);usedSize--;// 只用调整根节点所在的那一棵树，因为其他的树在之前已经调整过了shiftDown(0,usedSize);}

时间复杂度

向下调整算法时间复杂度:O(n)

算最坏的情况（每次调整都需要从根一直调整到倒数第二层）：
所以 每一层所需的次数就是 结点数 * (高度-1)
(结点数为2^h-1，高度为log₂(n+1) )
之后利用错位相减法求得O(n)

向上调整算法时间复杂度:O(n*log~2~n)

算最坏的情况（每次调整都需要从叶子一直调整到根）：
所以 每一层所需的次数就是 结点数 * 层数
(结点数为2^h-1，高度为log₂(n+1) ，高度也即层数)
之后利用错位相减法求得O(n)

手稿：