【题目来源】
http://oj.ecustacm.cn/problem.php?id=1780
http://oj.ecustacm.cn/viewnews.php?id=1023

【题目描述】
给出n个数字，你可以任意选择一些数字相乘，相乘之后得到新数字x。
其中，x的分数等于x不同质因子的数量。
请你计算所有选择数字方案中，x分数的总和。答案对1000000007取模。

【输入格式】
输入第一行为一个正整数n。
第二行包含n个正整数ai。(1≤n≤200000,1≤ai≤1000000)

【输出格式】
输出一个整数表示答案。即输出所有的质数在所有组合中出现的总次数。

【输入样例】
3
6 1 2

【输出样例】
10

【算法分析】
** 样例解析
针对本题中给出的包含 3 个数字的样例 {6, 1, 2}，共有 8 种组合：∅, {1}，{2}，{6}，{1,2}，{1,6}，{2,6}，{1,2,6}。每种组合内数字相乘得 {∅, 1, 2, 6, 1×2, 1×6, 2×6, 1×2×6}={∅, 1, 2, 2×3, 2, 2×3, 2×2×3, 2×2×3}，它们的质因子数量是 {0, 0, 1, 2, 1, 2, 2, 2}，总和是10。∅ 表示空集。
也就是说，从n个数中任选数字相乘，共有 2^n 种组合。由于本例中的 n 很大，所以直接调用pow() 库函数不可行，因为 pow() 不支持n超大的计算。另外，用位运算 2<<n 计算也不可取。所以，需要采用快速幂来计算 2^n。

** 快速幂（https://blog.csdn.net/hnjzsyjyj/article/details/132344391）
快速幂就是快速计算底数a的n次幂，其时间复杂度为O(log₂n)。
与朴素幂运算的时间复杂度O(n)相比，快速幂的计算效率有了极大的提高。
矩阵快速幂的思想和快速幂的思想是一样的。无非就是底数变为矩阵了。所以，在计算矩阵快速幂时，只需在代码中定义一下矩阵的乘法即可。
利用位运算实现快速幂，原理如下：
                     
即将十进制幂转换为二进制幂，然后利用二进制位间的倍增关系递推，达到快速计算幂的过程。
计算过程中，为了防止溢出，需要进行“取模”运算，其运算规则如下：
(a+b)%p=(a%p+b%p)%p
(a-b)%p=(a%p-b%p)%p
(a*b)%p=(a%p*b%p)%p
利用快速幂计算 a^n 的代码模板如下：

const int MOD=1e9+7;
typedef long long ll;
ll fastpow(ll a,ll n) {ll ans=1;while(n) {if(n&1) ans=ans*a%MOD;a=a*a%MOD;n>>=1;}return ans;
}

** 一个质数可能在多少个组合中出现？
一个质数在一个组合中出现一次，答案加1。统计所有的质数在所有组合中出现的总次数，就是本题所求答案。一个质数可能在多少个组合中出现？设 x 是其中 k 个数的因子，那么它将在 2^n−2^(n−k) 个组合中出现。
例如，在样例 {6,1,2} 中，质数2是 {6,2} 这2个数的因子，那么质数 2 将在 2^n−2^(n−k)=2^3-2^(3-2)=2^3-2^1=6 个组合中出现，即 {2,6,1×2,1×6,2×6,1×2×6}={2,2×3,2,2×3,2×2×3,2×2×3}。
又如，在样例 {6,1,2} 中，质数 3 是 {6} 的因子，那么质数 3 将在 2^n−2^(n−k)=2^3-2^(3-1)=2^3-2^2=4 个组合中出现，即 {6,1×6,2×6,1×2×6}={2,2×3,2×2×3,2×2×3} 。
答案是 6+4=10。

** 素数筛 <-- 欧拉筛（https://blog.csdn.net/hnjzsyjyj/article/details/132352060）
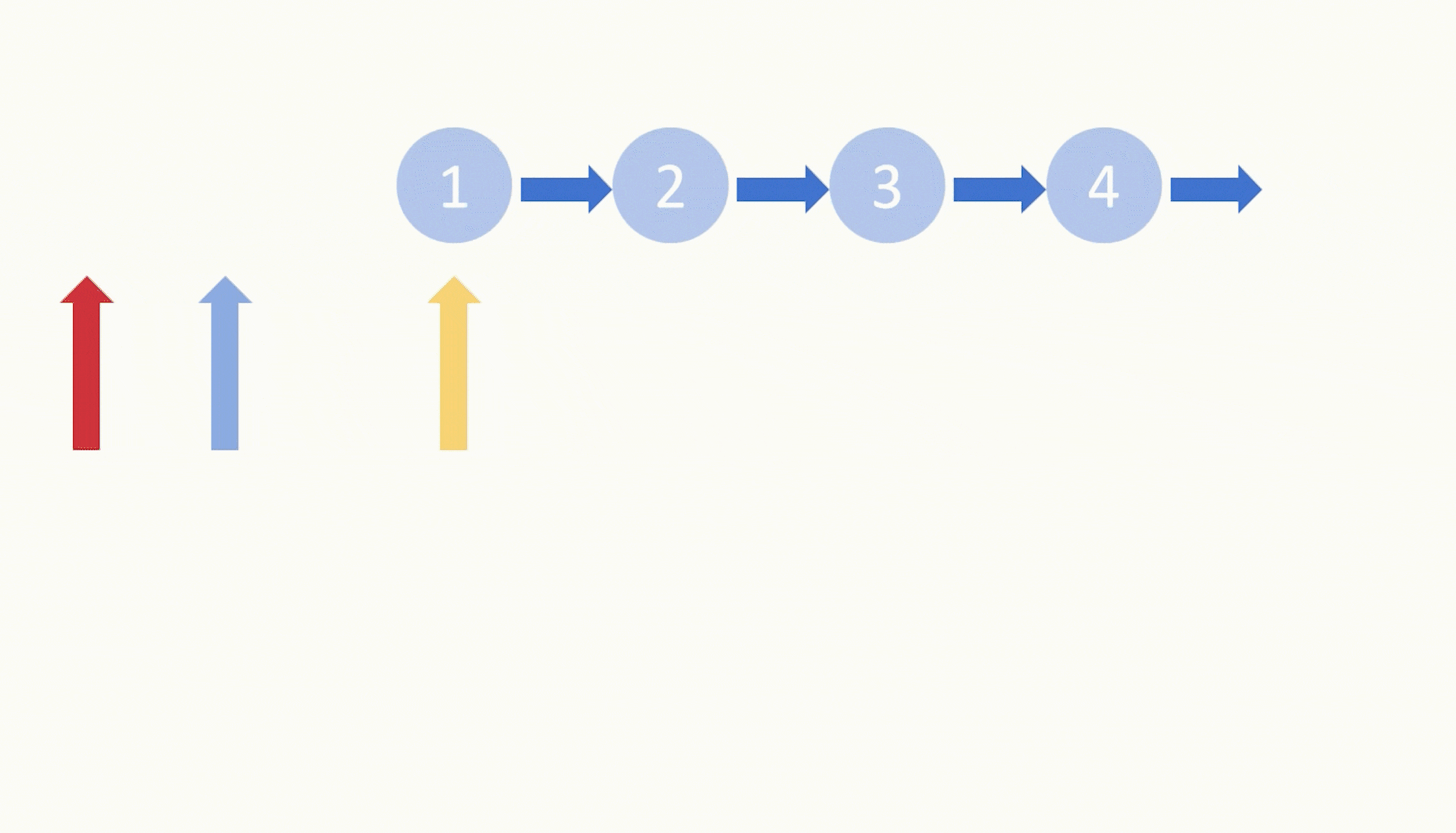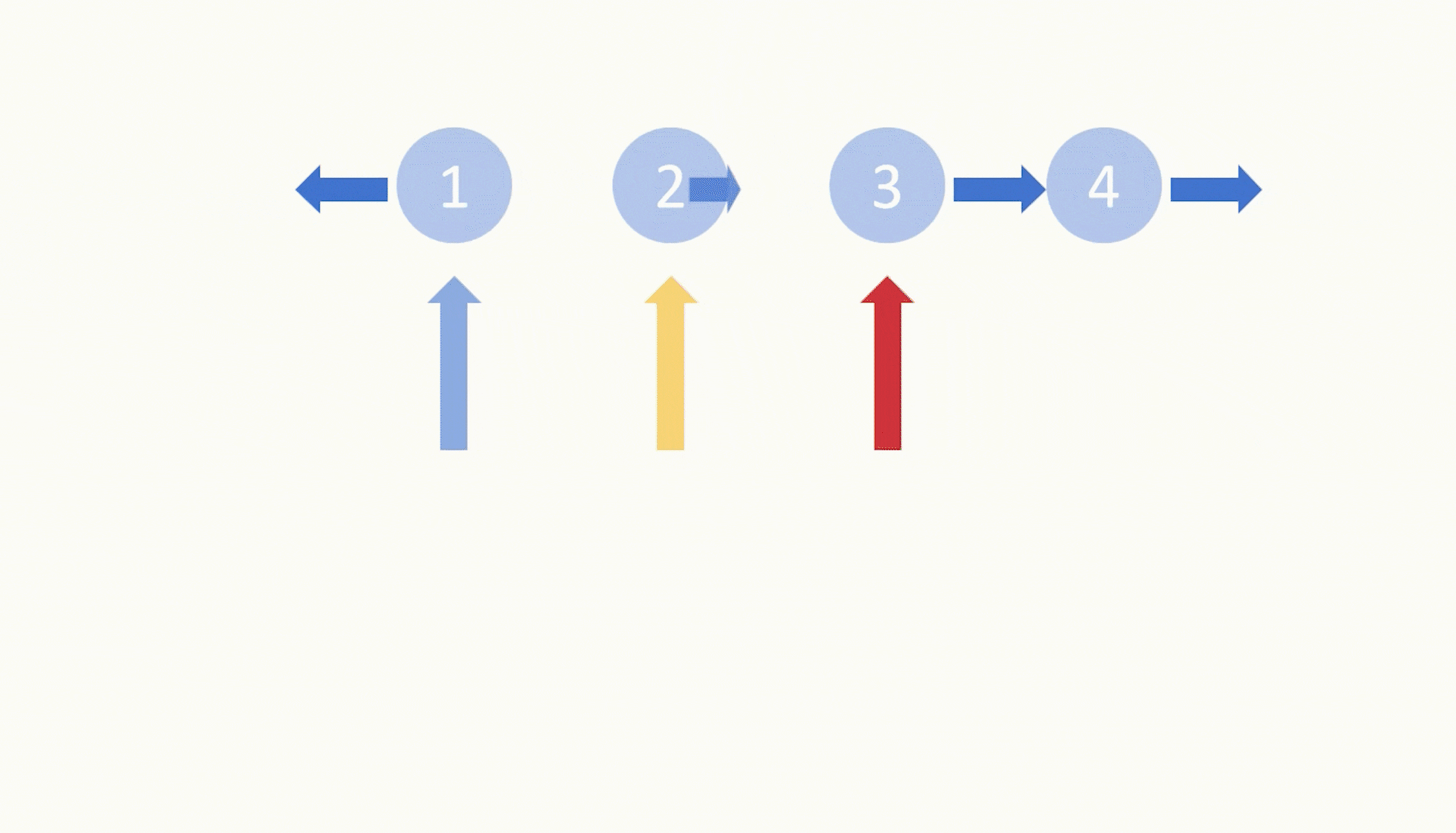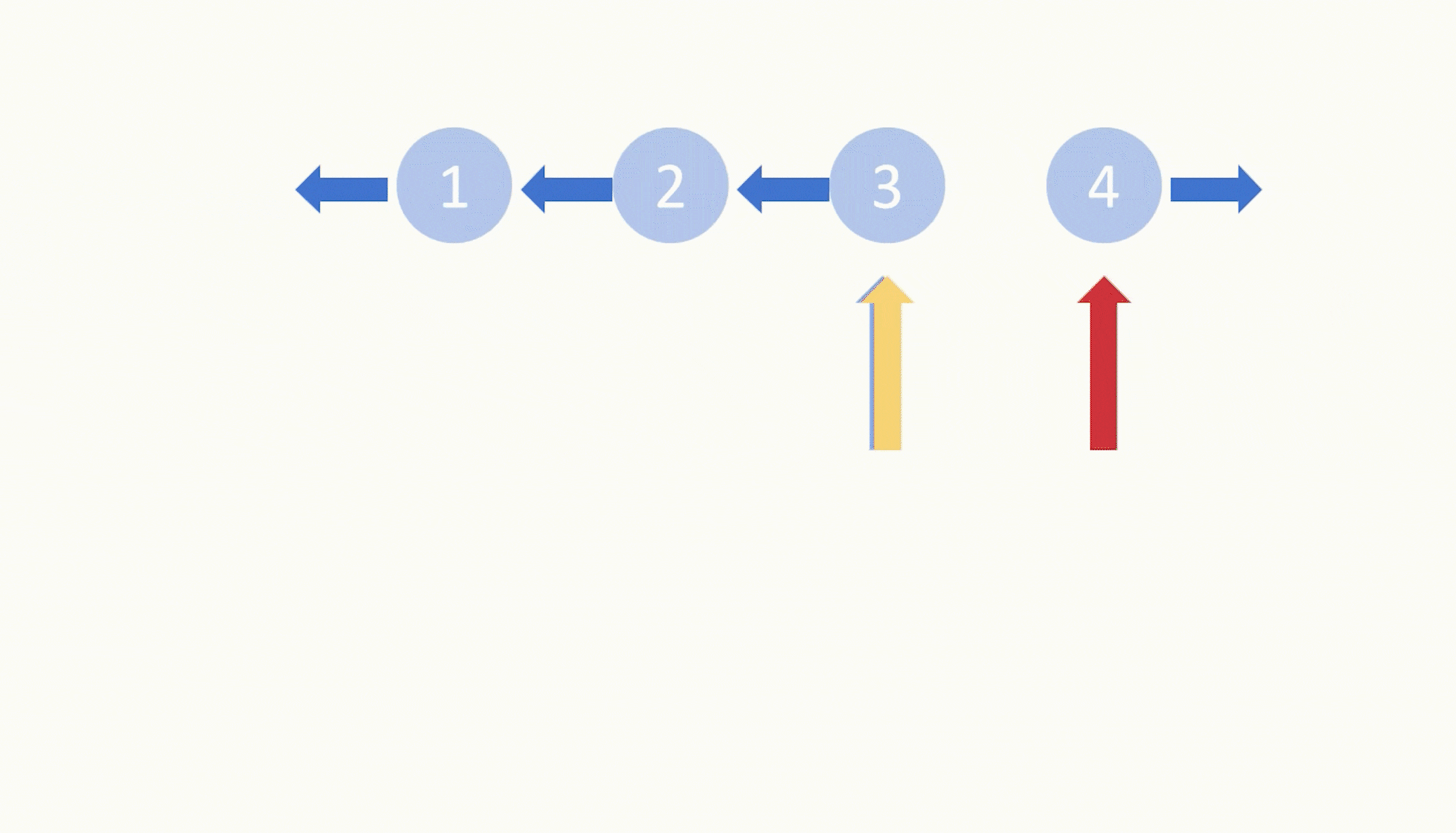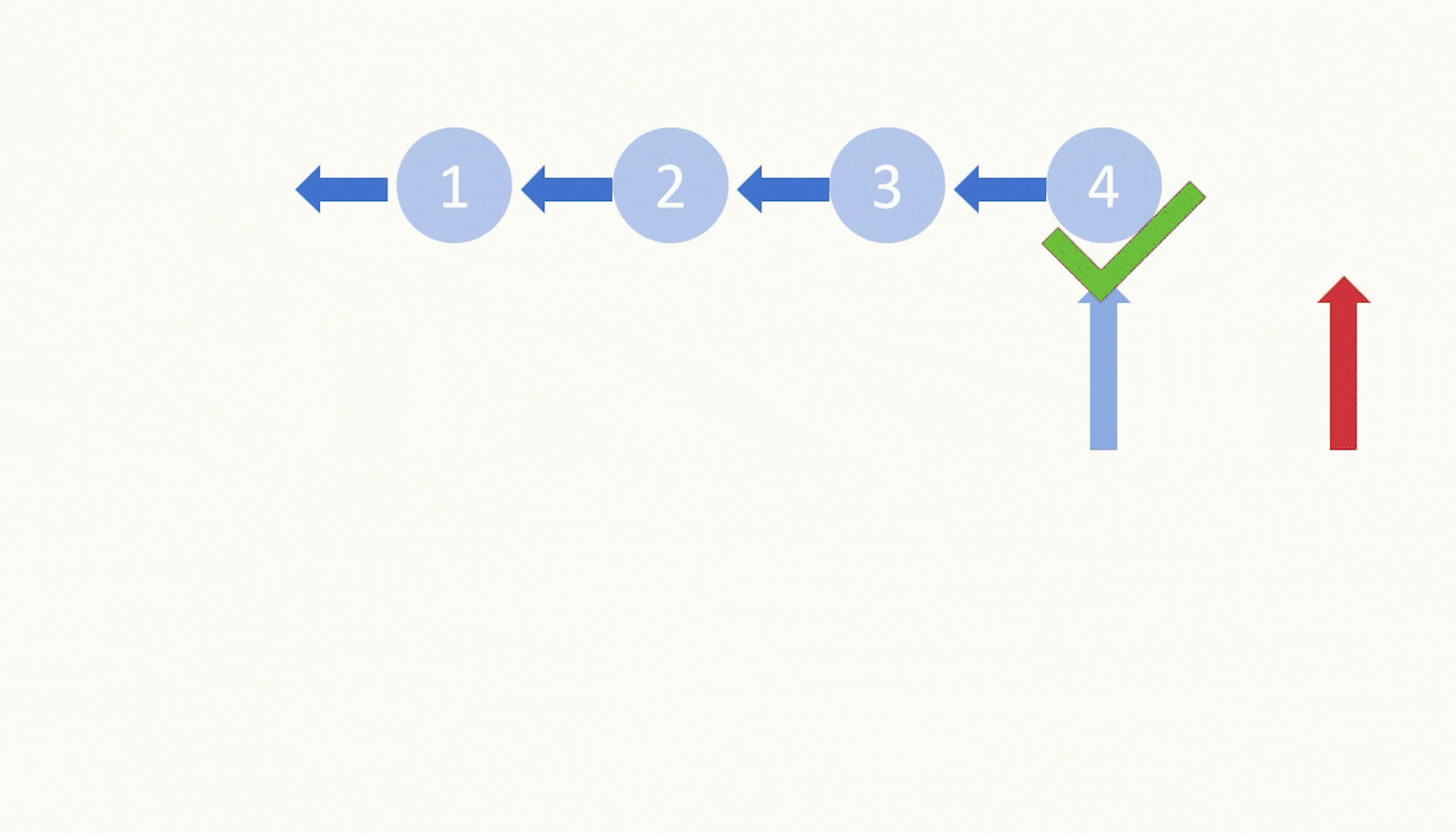
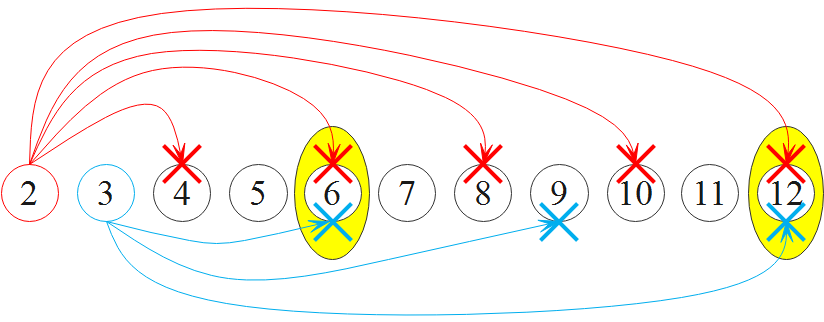
普通的素数筛法，即将给定的数 n 以内的所有数 x 的倍数 kx(k≥2) 都筛掉。
显然由下图可知，同一个数可能被多个素数重复筛掉。如下图中的 6、12 被重复筛掉。
这需要优化，欧拉筛便是一种素数的线性筛法。原理是让每个合数只被它的最小质因数筛掉，这样每个合数只会被筛选一次。

本题的解题步骤是：
* 用素数筛得到所有的质数（本例代码用的是普通筛法，未用欧拉筛）；
* 统计每个质数在 n 个数中出现的次数 k；
* 用 2^n-2^(n-k) 计算它在所有组合中的分数。

【算法代码】

#include <bits/stdc++.h>
using namespace std;const int maxn=1e6+5;
int cnt[maxn];
bool st[maxn];typedef long long ll;
const int MOD=1e9+7;
ll fastpow(ll a, ll n) {ll ans=1;while(n) {if(n&1) ans=ans*a%MOD;a=a*a%MOD;n>>=1;}return ans;
}int main() {int n;cin>>n;for(int i=1; i<=n; i++) {int a;scanf("%d",&a);cnt[a]++;}ll ans=0;for(int i=2; i<maxn; i++) {if(!st[i]) {ll k=cnt[i];for(int j=2*i; j<maxn; j+=i) {k+=cnt[j];st[j]=true;}if(k) {ans=(ans+fastpow(2,n)-fastpow(2,n-k)+MOD)%MOD;}}}cout<<ans<<endl;return 0;
}/*
in:
3
6 1 2out:
10
*/

【参考文献】
https://blog.csdn.net/weixin_43914593/article/details/131750902
https://blog.csdn.net/hnjzsyjyj/article/details/109556276
https://blog.csdn.net/qaqwqaqwq/article/details/123587336
https://zhuanlan.zhihu.com/p/494328631