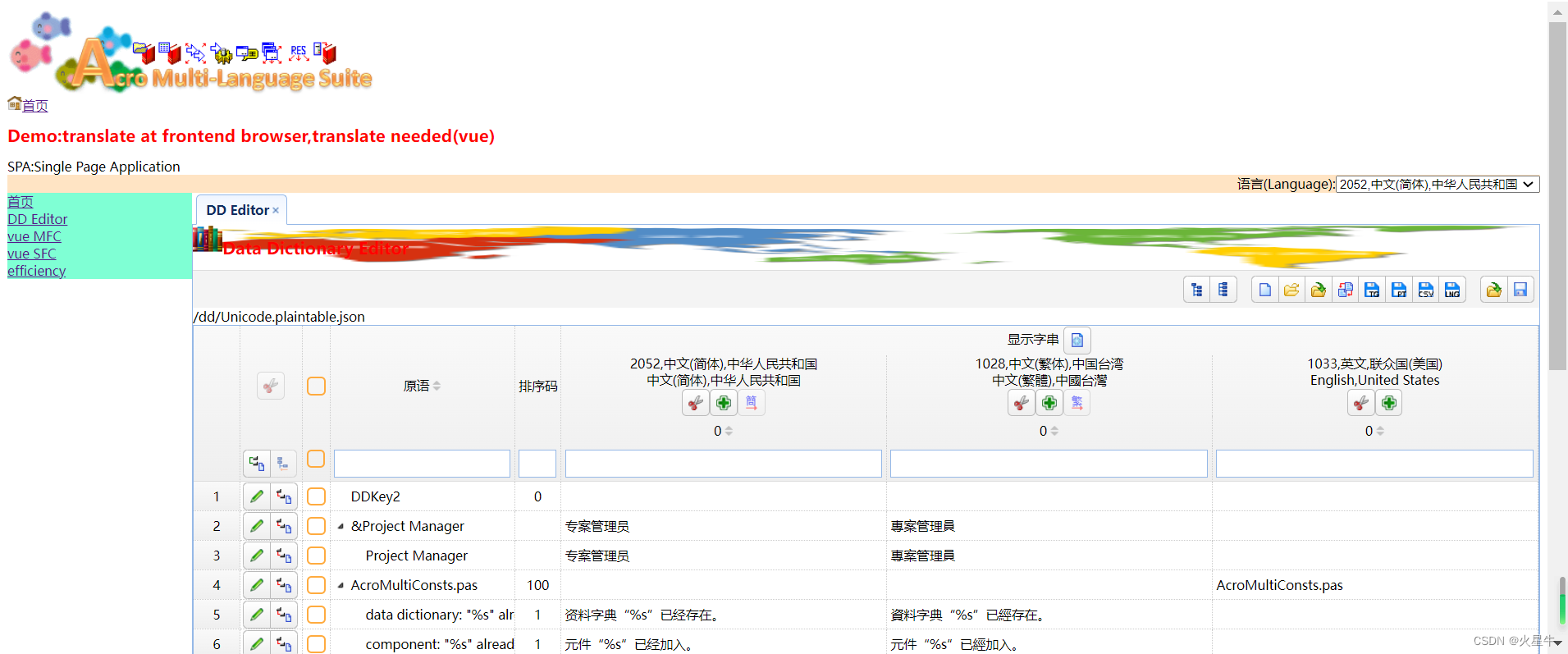
easyui显示编辑树形资料有TreeGrid元件,但是这个元件的vue版本和react版本没有分页功能。virtual scroll功能也表现不佳。
我用DataGrid来处理。要解决的问题点:
(1)如何显示成树形。即,子节点如何有缩进。
先计算好每个节点的层级level,然后template中设置缩进大小。
<template v-slot:body="{row,column,rowIndex}"><div v-Droppable="{dragEnter:onDDKeyDragEnter,drop:onDDKeyDrop}"v-Draggable="{row:row,proxy:$refs.DDKeyDragProxy,revert:true,axis:'v',dragStart:onDDKeyDragStart,dragEnd:onDDKeyDragEnd,drag:onDDKeyDrag}"@click="onDDKeyClick"><span class='tree-indent' :style='{width:(row.acroStates.level*16).toString()+"px"}'></span><span v-if="row.children && row.children.length>0" :class="getDDKeyExpanderClass(row)" @click="onRowToggle($event,row)"></span><span v-else class='tree-indent'></span><span class='tree-title'>{{row[column.field]}}</span></div>
</template>(2)如何展开和收拢节点。
展开收拢时,计算好每个节点的isVisual属性,通过DataGrid的filter来显示和隐藏。
expandRowRules:[{field:'isVisual',op:'equal',value:true
}],......
<DataGrid :filterRules="expandRowRules">
......
toggleRow(row){if (row.acroStates.state=='open') row.acroStates.state='closed';else row.acroStates.state='open';let root=row;function scanNodes(parent,children){ for(let i=0;i<children.length;i++){let node=children[i];node.isVisual=root.acroStates.state=='open' && parent.acroStates.state=='open';if (node.children) scanNodes(node,node.children);}}if (row.children) scanNodes(row,row.children);
},
......
onRowToggle(e,row){//console.log('toggle',e,row);//this.finishEditing();util_treePlain.toggleRow(row);this.$refs.tree.doFilter();//取消冒泡,使其不触发cellclick事件e.cancelBubble=true;e.preventDefault();e.stopPropagation();
},(3)排序时如何保持节点的上下级层级关系。
节点按同级排序,按深度优先扫描树形节点,把节点一个个加入到平面的数组中。
expandTree2Plain(treeRows){let rows=[];function scanNodes(nodes,level){for(let i=0;i<nodes.length;i++){let node=nodes[i];if (!node.acroStates){node.acroStates={state:'open'}}node.acroStates.level=level;node.acroStates.index=rows.length;node.isVisual=node.acroStates.state=='open';rows.push(node);if (node.children){scanNodes(node.children,level+1);}}}scanNodes(treeRows,0);return rows;
},
sortTree2Plain(treeRows,sorts){let rows=[];function scanNodes(nodes){if (sorts && sorts.length>0){nodes.sort(function(a,b){let r;let v1=a[sorts[0].field]; let v2=b[sorts[0].field];if (v1==null||v1==undefined) v1='';if (v2==null||v2==undefined) v2='';if (sorts[0].field=='SortNumber'){if (v1=='') v1=-1;else v1=parseInt(v1);if (v2=='') v2=-1;v2=parseInt(v2);}if (v1<v2) r=-1;else if (v1==v2) r=0;else r=1;if (sorts[0].order=='desc') r=-r;return r;});}for(let i=0;i<nodes.length;i++){let node=nodes[i];node.acroStates.index=rows.length;rows.push(node);if (node.children) scanNodes(node.children);}}scanNodes(treeRows);//console.log(rows);return rows;
},