前言

我们所熟知的快速排序和归并排序都是非常优秀的排序算法。

但是快速排序和归并排序的一个区别就是：快速排序是一种内部排序，而归并排序是一种外部排序。

简单理解归并排序：递归地拆分，回溯过程中，将排序结果进行合并。

大致流程示意图：

 

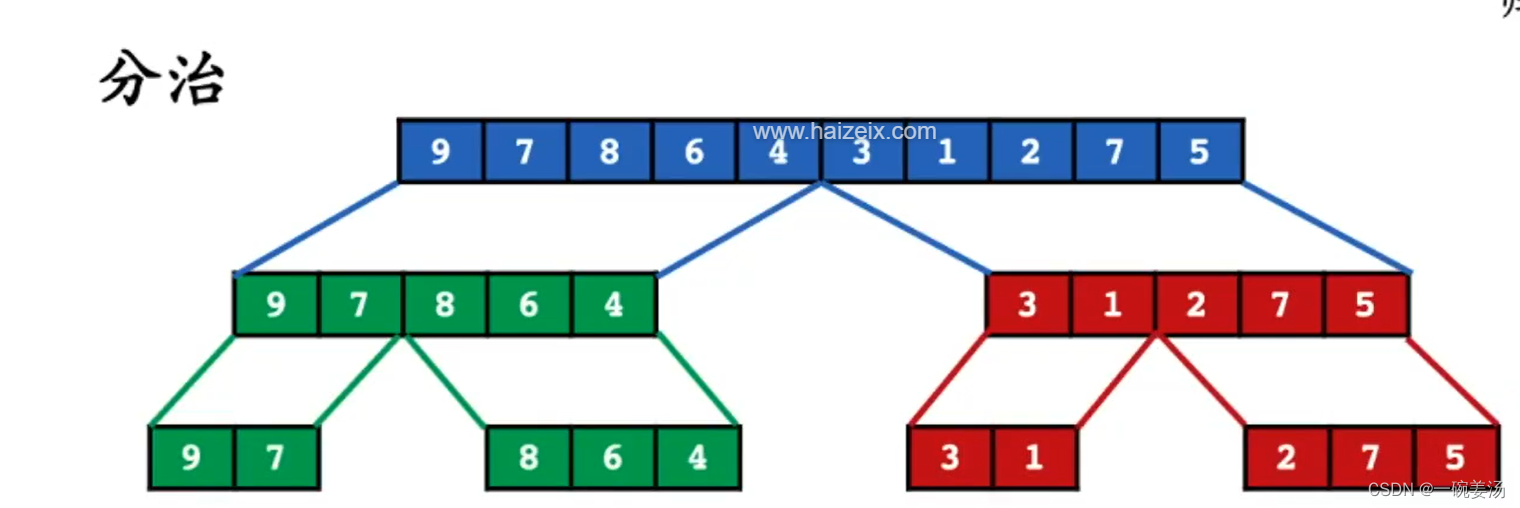
假设递归的终止条件就是剩下三个以下的元素就可以排序了。

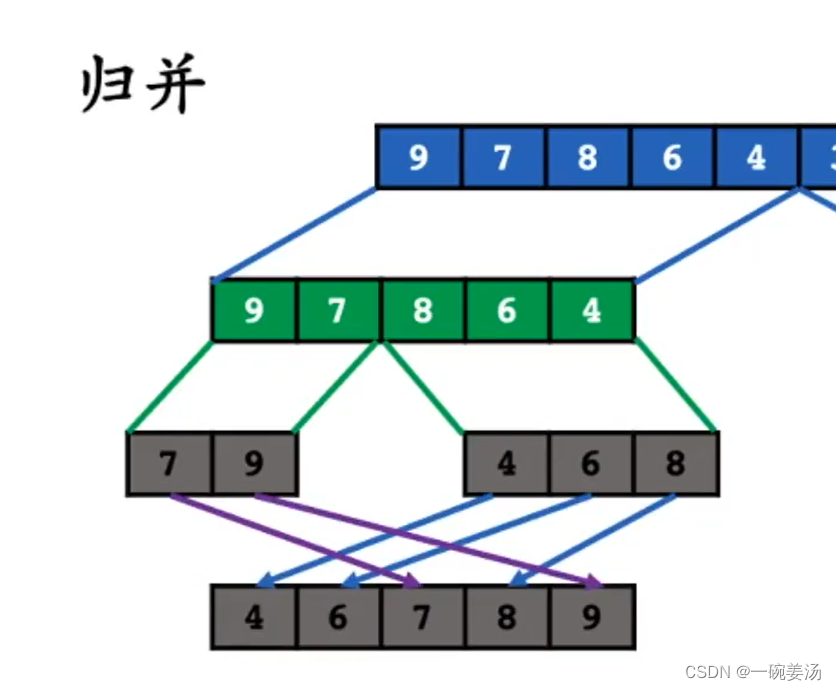
注意：这步合并的过程用到了额外的存储空间。完成了排序之后再复制回去。

二路归并演示代码

#include <iostream>
using namespace std;void merge_sort(int *arr, int l, int r) {// 递归终止条件：只有一个元素或者没有元素的时候，不需要排序。if (l >= r) return ;// 打印输出排序之前的情况cout << endl;cout << "sort " << l << "<-->" << r << " : ";for (int i = l; i <= r; i++) cout << arr[i] << " ";cout << endl;int mid = (l + r) >> 1;merge_sort(arr, l, mid); // left sortmerge_sort(arr, mid + 1, r); // right sort// 写递归代码，一定不要展开地看，上面两行代码就当做左右子区间已经排序好了。// 下面将对两个区间进行合并，需要开辟新的空间将元素存到temp数组中。int *temp = (int *)malloc(sizeof(int) * (r - l + 1));int k = 0, p1 = l, p2 = mid + 1;while (p1 <= mid || p2 <= r) {if ((p2 > r) || (p1 <= mid && arr[p1] <= arr[p2])) {// 只有当右边为空，或者左边不为空并且左边比右边小，才将左边的元素放入temp[k++] = arr[p1++];} else {temp[k++] = arr[p2++];}}// 最后再拷贝回去即可for (int i = l; i <= r; i++) arr[i] = temp[i - l];// 打印输出排序之后的情况for (int i = l; i <= r; i++) cout << arr[i] << " ";cout << endl;free(temp);return ;
}int main() {int n;int arr[100];cin >> n;for (int i = 0; i < n; i++) cin >> arr[i];merge_sort(arr, 0, n - 1);for (int i = 0; i < n; i++) cout << arr[i] << " ";return 0;
}

输入数据：

10 
7 9 0 8 6 4 5 3 1 2

输出：

sort 0<-->9 : 7 9 0 8 6 4 5 3 1 2 sort 0<-->4 : 7 9 0 8 6 sort 0<-->2 : 7 9 0 sort 0<-->1 : 7 9 
7 9 
0 7 9 sort 3<-->4 : 8 6
6 8
0 6 7 8 9sort 5<-->9 : 4 5 3 1 2sort 5<-->7 : 4 5 3sort 5<-->6 : 4 5
4 5
3 4 5sort 8<-->9 : 1 2
1 2
1 2 3 4 5
0 1 2 3 4 5 6 7 8 9
0 1 2 3 4 5 6 7 8 9

多路归并

上述演示代码的归并排序只是二路归并。将两个有序数组合并为一个有序数组。

那么多路归并就很好理解了，就是将多个有序数组合并为一个有序数组。

比如三路归并：

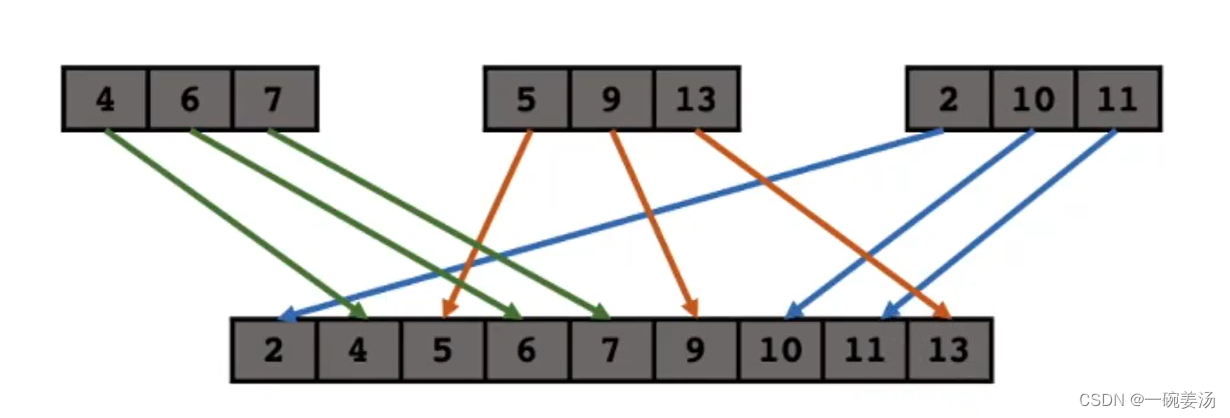
 关于多路归并排序的应用，有一道很经典的面试题：

意思就是：我的内存太小了，无法通过诸如快速排序这样的内部排序算法，进行数据的直接整体排序。那么为什么这个问题可以由归并算法来解决呢？

归并的时候，外存可以作为归并排序中的那片关键的额外空间，数据是可以直接写回外存的，所以不需要内存有40GB的额外空间来先存放排序完的数据，再写回外存。

其实这40GB的文件可以被拆分成20份2GB的小文件，我们只要分别对20份小文件进行排序之后，进行20路归并操作就可以了

注意：程序执行一定是在内存当中，所有的数据也都需要从辅存或者外存当中调入内存当中，才可以进行CPU的运算。一个2GB大小的内存当然无法调入40GB的数据。

还需注意的是：我们在程序中只存储了相应的文件指针，并没有将文件中的内容一次性全部读满内存，而是需要一个数据就从文件中读一个数据。

读取文件演示代码：

*************************************************************************> File Name: merge_file.cpp> Author: jby> Mail: > Created Time: Sat 12 Aug 2023 11:39:20 PM CST************************************************************************/#include<iostream>
using namespace std;int main(int argc, char *argv[]) {int n = argc - 1; // 读取文件数量FILE **farr = (FILE **)malloc(sizeof(FILE *) * n);for (int i = 1; i <= n; i++) {farr[i - 1] = fopen(argv[i], "r");}for (int i = 0; i < n; i++) {int a;while (~fscanf(farr[i], "%d", &a)) {printf("%d\n", a);}printf("======\n");}return 0;
}

生成俩数据文件：file1、file2

# file1
1
34
56
78

# file2:
3
45
89
100

执行命令行：$./a.out file1 file2

输出结果：

1
34
56
78
======
3
45
89
100
======

这样我们就依次读取了存放在两个文件中的数据。

文件排序演示代码（简单实现，不用归并）

/*************************************************************************> File Name: merge_file.cpp> Author: jby> Mail: > Created Time: Sat 12 Aug 2023 11:39:20 PM CST************************************************************************/#include<iostream>
using namespace std;struct Data {FILE *fin;     // fin: 当前文件指针int val, flag; // val: 当前读取的值；flag: 当前文件是否为空
};int main(int argc, char *argv[]) {int n = argc - 1; // 读取文件数量Data *data = (Data *)malloc(sizeof(Data) * n);for (int i = 1; i <= n; i++) {data[i - 1].fin = fopen(argv[i], "r");if (fscanf(data[i - 1].fin, "%d", &data[i - 1].val) == EOF) {data[i - 1].flag = 1;} else {data[i - 1].flag = 0;}}FILE *fout = fopen("output", "w");while (1) {int flag = 0;int ind = -1;int minVal = 0x3f3f3f3f;for (int i = 0; i < n; i++) {if (data[i].flag) continue; // 当前文件为空if (ind == -1 || data[i].val < data[ind].val) {ind = i;}}if (ind != -1) {fprintf(fout, "%d\n", data[ind].val); // 向结果文件中输出内容if (fscanf(data[ind].fin, "%d", &data[ind].val) == EOF) {data[ind].flag = 1;} else {data[ind].flag = 0;}flag = 1;}if (flag == 0) break;}return 0;
}

执行命令行：$./a.out file1 file2

输出结果，保存在output文件中：

1
3
34
45
56
78
89
100

归并排序的算法思想

我们不妨把思维从排序问题当中延展出来，归并排序的算法思想可以看成是以下三个步骤：

1. 左边处理一下，得到左边的信息
2. 右边处理一下，得到右边的信息
3. 最后再处理，横跨左右两边的信息

这就是分而治之的思想。

LeetCode刷题实战

剑指 Offer 51. 数组中的逆序对

在归并排序的过程中，当右边区间的元素放进额外空间的时候，左边剩下的元素个数就是该元素所对应的逆序对个数。所以可以在归并的过程中不断累加。

class Solution {
public:vector<int> temp;int countResult(vector<int>& nums, int l, int r) {if (l >= r) return 0; // 如果只有一个元素，逆序数为0int ans = 0, mid = (l + r) >> 1;ans += countResult(nums, l, mid);ans += countResult(nums, mid + 1, r);int k = l, p1 = l, p2 = mid + 1;while (p1 <= mid || p2 <= r) {if ((p2 > r) || (p1 <= mid && nums[p1] <= nums[p2])) {temp[k++] = nums[p1++];} else {temp[k++] = nums[p2++];ans += (mid - p1 + 1);}}for (int i = l; i <= r; i++) nums[i] = temp[i];return ans;}int reversePairs(vector<int>& nums) {while (temp.size() < nums.size()) temp.push_back(0);return countResult(nums, 0, nums.size() - 1);       }
};

23. 合并 K 个升序链表 - 力扣（LeetCode）

这道题其实跟之前的文件排序演示代码的逻辑没有本质区别，只不过这道题可以用到堆来加速。

class Solution {
public:struct CMP {bool operator()(ListNode *p, ListNode *q) {return p->val > q->val;}};ListNode* mergeKLists(vector<ListNode*>& lists) {priority_queue<ListNode *, vector<ListNode *>, CMP> q;for (auto x : lists) {if (x == nullptr) continue;q.push(x);}ListNode ret, *p = &ret;while (!q.empty()) {ListNode *cur = q.top();q.pop();p->next = cur;p = cur;if (cur->next) q.push(cur->next);}return ret.next;}
};

148. 排序链表 - 力扣（LeetCode）


 

如何用归并排序实现链表的排序呢？下面这段代码还是很具有典型意义的用链表来实现过程。

lass Solution {
public:ListNode *mergeSort(ListNode *head, int n) {if (head == nullptr || head->next == nullptr) return head;int l = n / 2, r = n - l;ListNode *lp = head, *rp = lp, *p;for (int i = 1; i < l; i++, rp = rp->next);p = rp, rp = rp->next;p->next = nullptr;lp = mergeSort(lp, l); // left Sortrp = mergeSort(rp, r); // right SortListNode ret;p = &ret;while (lp || rp) {if (rp == nullptr || (lp && lp->val < rp->val)) {p->next = lp;lp = lp->next;p = p->next;} else {p->next = rp;rp = rp->next;p = p->next;}}return ret.next;}ListNode* sortList(ListNode* head) {int n = 0;ListNode *p = head;while (p) p = p->next, n += 1;return mergeSort(head, n);}
};

1305. 两棵二叉搜索树中的所有元素 - 力扣（LeetCode）

用中序遍历，归并两颗子树，也是具有一定综合性的题。（怎么说的跟考研数学似的。。。）

class Solution {
public:void getResult(TreeNode *root, vector<int> &arr) {if (root == nullptr) return ;getResult(root->left, arr);arr.push_back(root->val);getResult(root->right, arr);return ;}vector<int> getAllElements(TreeNode* root1, TreeNode* root2) {vector<int> lnums, rnums;getResult(root1, lnums);getResult(root2, rnums);vector<int> ret;int p1 = 0, p2 = 0;while (p1 < lnums.size() || p2 < rnums.size()) {if (p2 >= rnums.size() || (p1 < lnums.size() && lnums[p1] < rnums[p2])) {ret.push_back(lnums[p1++]);} else {ret.push_back(rnums[p2++]);}}return ret;}
};

327. 区间和的个数 - 力扣（LeetCode）

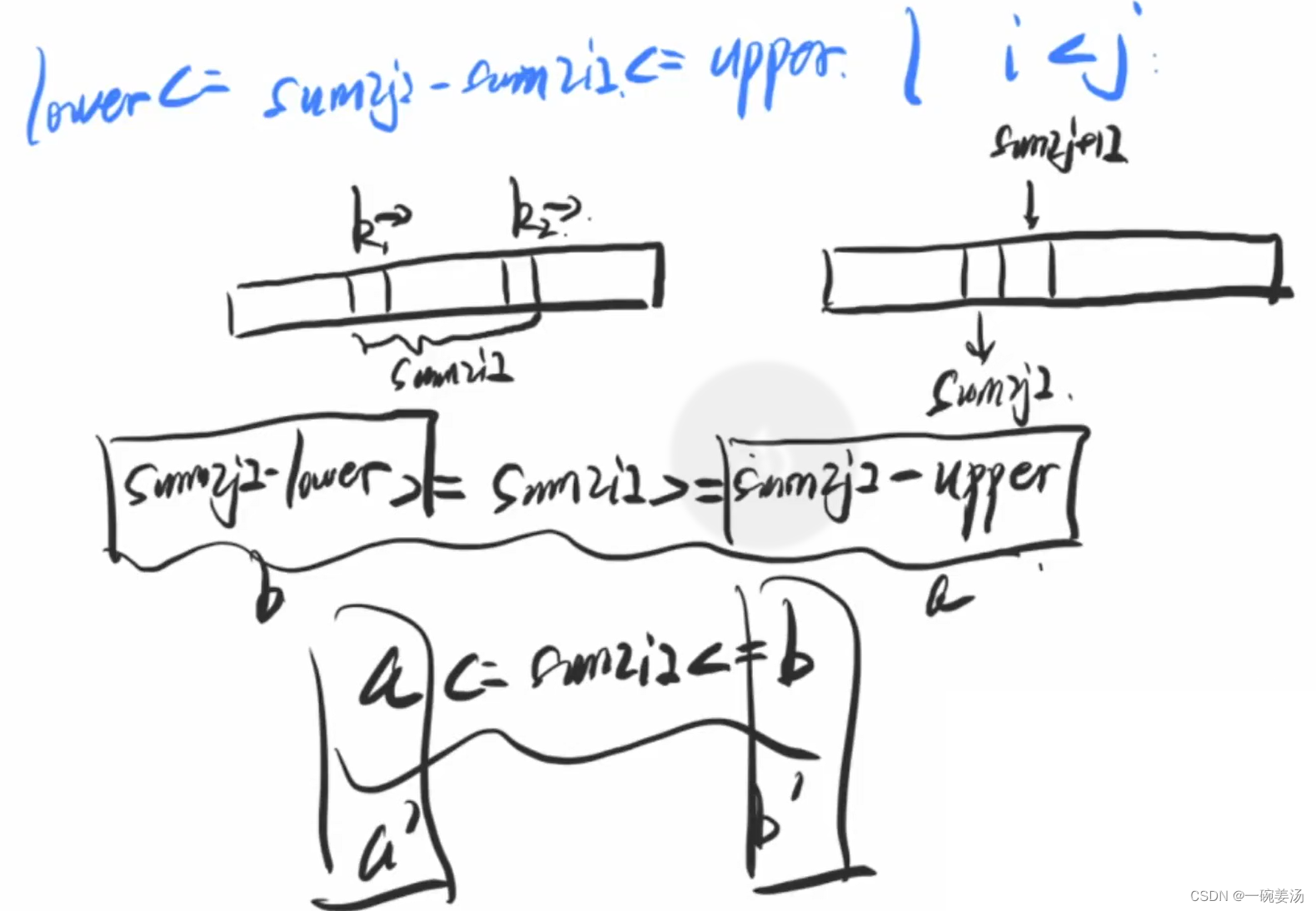
一说到区间和值，就能想到前缀和。区间和等于前缀和数组中两项相减的值。问题就变成了，前缀和数组中，有多少对 lower <= sun[i]-sum[j] <= upper (i>j)

利用左右区间的有序性，加速查找的过程。

算法解题过程的封装思维：当我们将问题转化成另一个问题的时候，我们就忘掉前面的问题到底是什么，只需专注解决当前这个独立的问题。而不是脑子里一团乱麻。

class Solution {
public:int countTwoPart(vector<long long> &sum, int l1, int r1, int l2, int r2, int lower, int upper) {int ans = 0, k1 = l1, k2 = l1;for (int j = l2; j <= r2; j++) {long long a = sum[j] - upper;long long b = sum[j] - lower;while (k1 <= r1 && sum[k1] < a) k1++;while (k2 <= r1 && sum[k2] <= b)k2++;ans += k2 - k1;}return ans;}int mergeSort(vector<long long> &sum, int l, int r, int lower, int upper) {if (l >= r) return 0; // 只有一个元素的话，根本找不到数值对。int mid = (l + r) >> 1, ans = 0;ans += mergeSort(sum, l, mid, lower, upper);ans += mergeSort(sum, mid + 1, r, lower, upper);ans += countTwoPart(sum, l, mid, mid + 1, r, lower, upper);int k = l, p1 = l, p2 = mid + 1;while (p1 <= mid || p2 <= r) {if (p2 > r || (p1 <= mid && sum[p1] < sum[p2])) {temp[k++] = sum[p1++];} else {temp[k++] = sum[p2++];}}for (int i = l; i <= r; i++) sum[i] = temp[i];return ans; }vector<long long> temp;int countRangeSum(vector<int>& nums, int lower, int upper) {vector<long long> sum(nums.size() + 1);while (temp.size() < sum.size()) temp.push_back(0);sum[0] = 0;for (int i = 0; i < nums.size(); i++) sum[i + 1] = sum[i] + nums[i];return mergeSort(sum, 0, sum.size() - 1, lower, upper);}
};

本质上还是利用了分治的思想。核心的过程就是如何计算跨左右两半部分的过程

315. 计算右侧小于当前元素的个数 - 力扣（LeetCode）

已经求得左右半边各自比它小的元素。两个区间合并。

class Solution {
public:// 归并排序的思想：分两个区间，统计两个区间的性质。// 在归并的过程中，左右两个有序区间，合并的时候，从大到小的顺序排，左边区间内，如果元素大于右边，则左边的元素比他小的个数应当加上右边r-p2+1struct Data {Data(int val, int ind) : val(val), ind(ind), cnt(0) {}bool operator > (const Data &a) {return val > a.val;}int val, ind, cnt;};void mergeSort(vector<Data> &arr, int l, int r) {if (l >= r) return ; // 如果只剩下一个元素，那就计算不了左右两边的统计性质int mid = (l + r) >> 1;mergeSort(arr, l, mid);mergeSort(arr, mid + 1, r);int k = l, p1 = l, p2 = mid + 1;while (p1 <= mid || p2 <= r) {if (p2 > r || (p1 <= mid && arr[p1] > arr[p2])) {arr[p1].cnt += r - p2 + 1;temp[k++] = arr[p1++];} else {temp[k++] = arr[p2++];}}for (int i = l; i <= r; i++) arr[i] = temp[i];return ;}vector<Data> temp;vector<int> countSmaller(vector<int>& nums) {vector<Data> arr;for (int i = 0; i < nums.size(); i++) arr.push_back(Data{nums[i], i});while (temp.size() < nums.size()) temp.push_back(Data{0, 0});mergeSort(arr, 0, arr.size() - 1);vector<int> ret(nums.size());for (auto x : arr) ret[x.ind] = x.cnt;return ret;}
};