设函数 f ( x ) f(\boldsymbol{x}) f(x), x ∈ R n \boldsymbol{x}\in\text{ℝ}^n x∈Rn二阶连续可微,记 g ( x ) = ∇ f ( x ) \boldsymbol{g}(\boldsymbol{x})=\nabla f(\boldsymbol{x}) g(x)=∇f(x), H ( x ) = ∇ 2 f ( x ) \boldsymbol{H}(\boldsymbol{x})=\nabla^2f(\boldsymbol{x}) H(x)=∇2f(x)。由于 H ( x ) \boldsymbol{H}(\boldsymbol{x}) H(x)连续,故 H ⊤ ( x ) = H ( x ) \boldsymbol{H}^\top(\boldsymbol{x})=\boldsymbol{H}(\boldsymbol{x}) H⊤(x)=H(x),即 H ( x ) \boldsymbol{H}(\boldsymbol{x}) H(x)是一个对称矩阵。若 f ( x ) f(\boldsymbol{x}) f(x)有极小值点 x 0 \boldsymbol{x}_0 x0,则在 x 0 \boldsymbol{x}_0 x0的近旁 H ( x ) \boldsymbol{H}(\boldsymbol{x}) H(x)是正定的。对具有连续Hesse阵的函数 f ( x ) f(\boldsymbol{x}) f(x), x 0 \boldsymbol{x}_0 x0近旁点 x k \boldsymbol{x}_k xk处的二阶泰勒展开式为
f ( x ) = f ( x k ) + g k ⊤ ( x − x k ) + 1 2 ( x − x k ) ⊤ H k ( x − x k ) + o ( ∥ x − x k ∥ 2 ) . f(\boldsymbol{x})=f(\boldsymbol{x}_k)+g_k^\top(\boldsymbol{x}-\boldsymbol{x}_k)+\frac{1}{2}(\boldsymbol{x}-\boldsymbol{x}_k)^\top\boldsymbol{H}_k(\boldsymbol{x}-\boldsymbol{x}_k)+o(\lVert\boldsymbol{x}-\boldsymbol{x}_k\rVert^2). f(x)=f(xk)+gk⊤(x−xk)+21(x−xk)⊤Hk(x−xk)+o(∥x−xk∥2).
其中, g k = ∇ f ( x k ) \boldsymbol{g}_k=\nabla f(\boldsymbol{x}_k) gk=∇f(xk), H k = H ( x k ) = ∇ 2 f ( x k ) \boldsymbol{H}_k=\boldsymbol{H}(\boldsymbol{x}_k)=\nabla^2f(\boldsymbol{x}_k) Hk=H(xk)=∇2f(xk)。令
q k ( x ) = f ( x k ) + g k ⊤ ( x − x k ) + 1 2 ( x − x k ) ⊤ H k ( x − x k ) q_k(\boldsymbol{x})=f(\boldsymbol{x}_k)+\boldsymbol{g}_k^\top(\boldsymbol{x}-\boldsymbol{x}_k)+\frac{1}{2}(\boldsymbol{x}-\boldsymbol{x}_k)^\top\boldsymbol{H}_k(\boldsymbol{x}-\boldsymbol{x}_k) qk(x)=f(xk)+gk⊤(x−xk)+21(x−xk)⊤Hk(x−xk)
则 q k ( x k ) = f ( x k ) q_k(\boldsymbol{x}_k)=f(\boldsymbol{x}_k) qk(xk)=f(xk), ∇ q k ( x k ) = ∇ f ( x k ) \nabla q_k(\boldsymbol{x}_k)=\nabla f(\boldsymbol{x}_k) ∇qk(xk)=∇f(xk), ∇ 2 q k ( x k ) = ∇ 2 f ( x k ) \nabla^2q_k(\boldsymbol{x}_k)=\nabla^2f(\boldsymbol{x}_k) ∇2qk(xk)=∇2f(xk)。因此当 x \boldsymbol{x} x在 x k \boldsymbol{x}_k xk近旁时,可用二次型函数 q k ( x ) q_k(\boldsymbol{x}) qk(x)作为 f ( x ) f(\boldsymbol{x}) f(x)的近似表示。由 ∇ 2 q k ( x k ) = ∇ 2 f ( x k ) = H k \nabla^2q_k(\boldsymbol{x}_k)=\nabla^2f(\boldsymbol{x}_k)=\boldsymbol{H}_k ∇2qk(xk)=∇2f(xk)=Hk的正定性知二次型函数 q k ( x ) q_k(\boldsymbol{x}) qk(x)有唯一最小值点。由于 q k ( x ) q_k(\boldsymbol{x}) qk(x)二阶连续可微,故其最小值点必为其驻点: o = q k ′ ( x ) = ∇ q k ( x ) = ∇ f ( x k ) + ∇ 2 f ( x k ) ( x − x k ) = g k + H k x − H k x k \boldsymbol{o}=q'_k(\boldsymbol{x})=\nabla q_k(\boldsymbol{x})=\nabla f(\boldsymbol{x}_k)+\nabla^2f(\boldsymbol{x}_k)(\boldsymbol{x}-\boldsymbol{x}_k)=\boldsymbol{g}_k+\boldsymbol{H}_k\boldsymbol{x}-\boldsymbol{H}_k\boldsymbol{x}_k o=qk′(x)=∇qk(x)=∇f(xk)+∇2f(xk)(x−xk)=gk+Hkx−Hkxk。即 q k ( x ) q_k(\boldsymbol{x}) qk(x)的驻点 x k + 1 \boldsymbol{x}_{k+1} xk+1满足
H k x k + 1 = H k x k − g k . \boldsymbol{H}_k\boldsymbol{x}_{k+1}=\boldsymbol{H}_k\boldsymbol{x}_k-\boldsymbol{g}_k. Hkxk+1=Hkxk−gk.
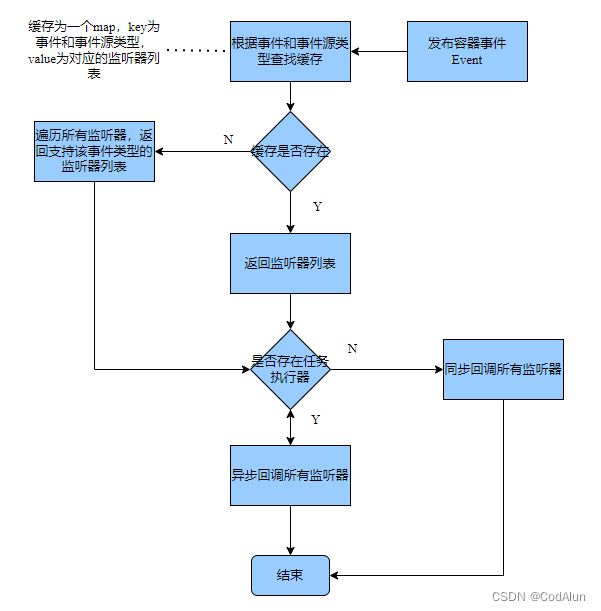
由 H k \boldsymbol{H}_k Hk的正定性知 H k \boldsymbol{H}_k Hk可逆,故由上式可解得 q k ( x ) q_k(\boldsymbol{x}) qk(x)的最小值点(如下图所示)
x k + 1 = x k − H k − 1 g k . ( 1 ) \boldsymbol{x}_{k+1}=\boldsymbol{x}_k-\boldsymbol{H}_k^{-1}\boldsymbol{g}_k.\quad\quad(1) xk+1=xk−Hk−1gk.(1)

在对目标函数 f ( x ) f(\boldsymbol{x}) f(x)如上描述的条件下,式(1)构成搜索 f ( x ) f(\boldsymbol{x}) f(x)的最优解 x 0 \boldsymbol{x}_0 x0的迭代式:初始时,在 x 0 \boldsymbol{x}_0 x0的近旁任取点 x 1 \boldsymbol{x}_1 x1,此时可保证 f ( x ) f(\boldsymbol{x}) f(x)在 x 1 \boldsymbol{x}_1 x1处的Hesse阵 H 1 = ∇ 2 f ( x 1 ) \boldsymbol{H}_1=\nabla^2f(\boldsymbol{x}_1) H1=∇2f(x1)是正定的。若 x 1 = x 0 \boldsymbol{x}_1=\boldsymbol{x}_0 x1=x0,则得到了最优解 x 1 = x 0 \boldsymbol{x}_1=\boldsymbol{x}_0 x1=x0。否则按式(1)可算得点 x 2 = x 1 − H 1 − 1 g k \boldsymbol{x}_2=\boldsymbol{x}_1-\boldsymbol{H}_1^{-1}\boldsymbol{g}_k x2=x1−H1−1gk。由于 x 2 \boldsymbol{x}_2 x2是 q 1 ( x ) q_1(\boldsymbol{x}) q1(x)的最小值点,故 q 1 ( x ) q_1(\boldsymbol{x}) q1(x)从 x 1 \boldsymbol{x}_1 x1到 x 2 \boldsymbol{x}_2 x2函数值是下降的。由 f ( x ) f(\boldsymbol{x}) f(x)与 q 1 ( x ) q_1(\boldsymbol{x}) q1(x)在 x 1 \boldsymbol{x}_1 x1处的相近性可知 f ( x ) f(\boldsymbol{x}) f(x)从 x 1 \boldsymbol{x}_1 x1到 x 2 \boldsymbol{x}_2 x2函数值也是下降的,故可望 x 2 \boldsymbol{x}_2 x2比 x 1 \boldsymbol{x}_1 x1更接近 x 0 \boldsymbol{x}_0 x0。若 ∇ f ( x 2 ) = o \nabla f(\boldsymbol{x}_2)=\boldsymbol{o} ∇f(x2)=o,则按 f ( x ) f(\boldsymbol{x}) f(x)所具有的
单峰性知,我们得到了最优解 x 2 = x 0 \boldsymbol{x}_2=\boldsymbol{x}_0 x2=x0。否则,可由式(1)计算 x 3 \boldsymbol{x}_3 x3,……,按此方式算得点 x k \boldsymbol{x}_k xk,且 x k \boldsymbol{x}_k xk位于 x 0 \boldsymbol{x}_0 x0的近旁。若此时 ∇ f ( x k ) = o \nabla f(\boldsymbol{x}_k)=\boldsymbol{o} ∇f(xk)=o,则得到最优解 x k = x 0 \boldsymbol{x}_k=\boldsymbol{x}_0 xk=x0。否则,可由式(1)算得更接近 x 0 \boldsymbol{x}_0 x0的点 x k + 1 = x k − H k − 1 g k \boldsymbol{x}_{k+1}=\boldsymbol{x}_k-\boldsymbol{H}_k^{-1}\boldsymbol{g}_k xk+1=xk−Hk−1gk,如上图所示。用这样的方法计算目标函数最优解的迭代序列算法称为牛顿法。
下列代码实现牛顿算法。
import numpy as np #导入numpy
from scipy.optimize import OptimizeResult #导入OptimizeResult
def newton(f, x1, gtol, **options):xk=x1gk=grad(f,xk)Hk=hess(f,xk)k=1while np.linalg.norm(gk)>=gtol:xk-=np.matmul(np.linalg.inv(Hk),gk)gk=grad(f,xk)Hk=hess(f,xk)k+=1bestx=xkbesty=f(bestx)return OptimizeResult(fun=besty, x=bestx, nit=k)
程序的第3~15行定义的newton函数实现牛顿算法。参数f,x1,gtol分别表示目标函数 f ( x ) f(\boldsymbol{x}) f(x),初始点 x 1 \boldsymbol{x}_1 x1和容错误差 ε \varepsilon ε,options实现minimize与本函数的信息交换机制。
第4~7行执行初始化操作:第4行将表示迭代点的xk初始化为x1。第5、6行分别调用函数grad和hess(详见博文《最优化方法Python计算:n元函数梯度与Hesse阵的数值计算》)计算目标函数 f ( x ) f(\boldsymbol{x}) f(x)在当前点 x 1 \boldsymbol{x}_1 x1处的梯度 ∇ f ( x 1 ) \nabla f(\boldsymbol{x}_1) ∇f(x1)和Hesse矩阵 ∇ 2 f ( x 1 ) \nabla^2f(\boldsymbol{x}_1) ∇2f(x1),赋予gk和Hk。第7行将迭代次数k初始化为1。
第8~12行的while循环执行迭代操作:第9行按式(1)
x k + 1 = x k − H k − 1 g k \boldsymbol{x}_{k+1}=\boldsymbol{x}_k-\boldsymbol{H}_k^{-1}\boldsymbol{g}_k xk+1=xk−Hk−1gk
计算迭代点更新xk。其中调用numpy.linalg的inv函数计算 H \boldsymbol{H} H的逆矩阵 H k − 1 \boldsymbol{H}_k^{-1} Hk−1,调用numpy的matmul函数计算矩阵的积 H k − 1 g k \boldsymbol{H}_k^{-1}\boldsymbol{g}_k Hk−1gk。第10、11行调用grad函数和hess函数计算 ∇ f ( x k + 1 ) \nabla f(\boldsymbol{x}_{k+1}) ∇f(xk+1)和Hesse矩阵 ∇ 2 f ( x k + 1 ) \nabla^2f(\boldsymbol{x}_{k+1}) ∇2f(xk+1)更新gk和Hk。第12行将迭代次数k自增1。循环往复,直至条件
∥ g k ∥ < ε \lVert\boldsymbol{g}_k\rVert<\varepsilon ∥gk∥<ε
成立为止。
第13~15行用 f ( x k ) f(\boldsymbol{x}_k) f(xk), x k \boldsymbol{x}_k xk及 k k k构造OptimizeResult(第2行导入)对象并返回。
例1 给定 ε = 1 0 − 8 \varepsilon=10^{-8} ε=10−8为容错误差,分别以 ( 0 0 ) \begin{pmatrix}0\\0\end{pmatrix} (00)和 ( − 1.2 1 ) \begin{pmatrix}-1.2\\1\end{pmatrix} (−1.21)作为初始点 x 1 \boldsymbol{x}_1 x1,用newton函数计算Rosenbrock函数的最优解。
解:下列代码完成计算。
import numpy as np #导入numpy
from scipy.optimize import minimize, rosen #导入minimize, rosen
x1=np.array([0,0]) #设置初始点
res=minimize(rosen, x1,method=newton, options={'gtol':1e-8}) #计算最优解
print(res)
x1=np.array([-1.2,1]) #设置初始点
res=minimize(rosen, x1,method=newton, options={'gtol':1e-8}) #计算最优解
print(res)
程序的第3~ 4行及第6~7行分别以 ( 0 0 ) \begin{pmatrix}0\\0\end{pmatrix} (00)和 ( − 1.2 1 ) \begin{pmatrix}-1.2\\1\end{pmatrix} (−1.21)作为初始点 x 1 \boldsymbol{x}_1 x1调用minimize传递newton计算Rosenbrock函数容错误差为 1 0 − 8 10^{-8} 10−8的最优解近似值。运行程序,输出
fun: 6.156132219000243e-22nit: 7x: array([1., 1.])fun: 1.4934237207405332e-18nit: 11x: array([1., 1.])
前3行表示从 x 1 = ( 0 0 ) \boldsymbol{x}_1=\begin{pmatrix}0\\0\end{pmatrix} x1=(00)起,迭代7次,newton算得最优解 ( 1 1 ) \begin{pmatrix}1\\1\end{pmatrix} (11),后3行则表示newton从 x 1 = ( − 1.2 1 ) \boldsymbol{x}_1=\begin{pmatrix}-1.2\\1\end{pmatrix} x1=(−1.21)起,迭代11次,算得最优解。读者可以相同起点及容错误差用FR共轭梯度算法计算Rossenbrock函数的最优解的结果相比较,将看到牛顿算法比FR共轭梯度法(详见博文《最优化方法Python计算:非二次型共轭梯度算法》)计算(对两个不同的初始点,在相同的容错误差下分别迭代24次和20次)效率更高。