LeetCode 周赛上分之旅 #40 结合特征压缩的数位 DP 问题

⭐️ 本文已收录到 AndroidFamily，技术和职场问题，请关注公众号 [彭旭锐] 和 BaguTree Pro 知识星球提问。

学习数据结构与算法的关键在于掌握问题背后的算法思维框架，你的思考越抽象，它能覆盖的问题域就越广，理解难度也更复杂。在这个专栏里，小彭与你分享每场 LeetCode 周赛的解题报告，一起体会上分之旅。

本文是 LeetCode 上分之旅系列的第 40 篇文章，往期回顾请移步到文章末尾~

双周赛 111

T1. 统计和小于目标的下标对数目（Easy）

标签：模拟、排序、相向双指针

T2. 循环增长使字符串子序列等于另一个字符串（Medium）

标签：排序、双指针

T3. 将三个组排序（Medium）

标签：状态机 DP、LIS 问题、贪心、二分查找

T4. 范围中美丽整数的数目（Hard）

标签：数位 DP、记忆化

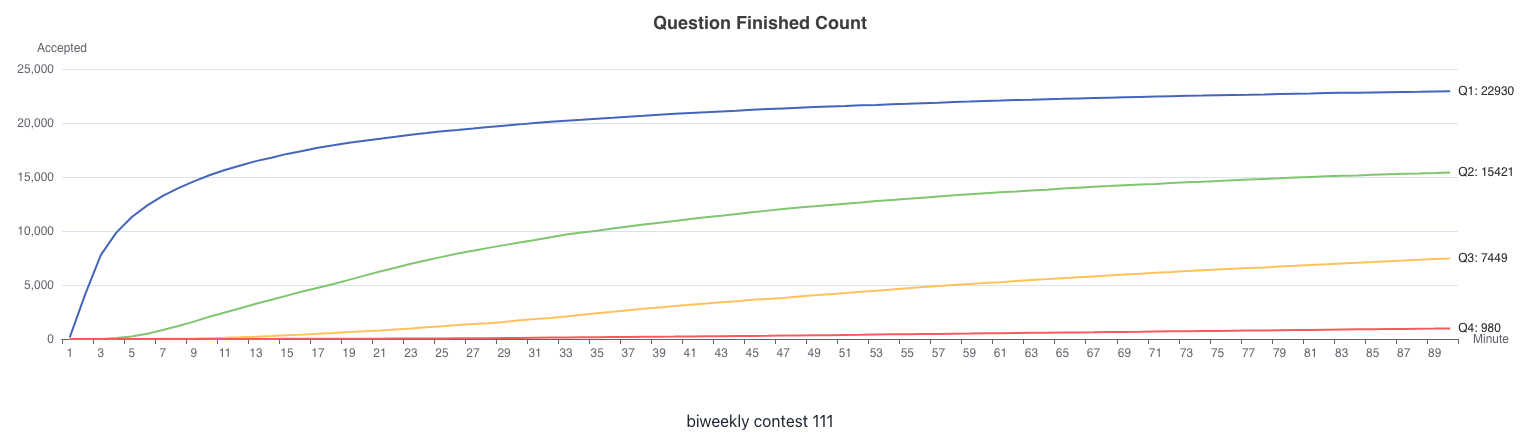
T1. 统计和小于目标的下标对数目（Easy）

https://leetcode.cn/problems/count-pairs-whose-sum-is-less-than-target/

题解一（模拟）

简单模拟题。

class Solution {fun countPairs(nums: List<Int>, target: Int): Int {var ret = 0for (i in 0 until nums.size) {for (j in i + 1 until nums.size) {if (nums[i] + nums[j] < target) ret ++}}return ret}
}

复杂度分析：

时间复杂度： $O(n^2)$
空间复杂度： $O (1)$

题解二（排序 + 相向双指针）

在题解一中存在很多无意义的比较，我们观察到配对的顺序是无关的，因此可以考虑利用有序性优化时间复杂度。

先对数组排序；
利用元素的大小关系，使用双指针筛选满足条件的配对数。

class Solution {fun countPairs(nums: MutableList<Int>, target: Int): Int {nums.sort()var ret = 0var i = 0var j = nums.size - 1while (i < j) {while (i < j && nums[i] + nums[j] >= target) {j--}if (i == j) breakret += j - ii++}return ret}
}

复杂度分析：

时间复杂度： $O (n l g n)$ 瓶颈在排序，双指针时间复杂度为 $O (n)$ ；
空间复杂度： $O (l g n)$ 排序递归栈空间。

T2. 循环增长使字符串子序列等于另一个字符串（Medium）

https://leetcode.cn/problems/make-string-a-subsequence-using-cyclic-increments/

题解（双指针 + 贪心）

首先阅读题意，问题相当于从 str1 中选择若干个位置执行 +1 操作后让 str2 成为 str1 的子序列。其次容易想到贪心算法，对于 str1[i] 与 str2[j] 来说，如果 str1[i] 能够在至多操作 1 次的情况下变为 str2[j]，那么让 i 与 j 匹配是最优的。

class Solution {fun canMakeSubsequence(str1: String, str2: String): Boolean {val U = 26val n = str1.lengthval m = str2.lengthvar j = 0for (i in 0 until n) {val x = str1[i] - 'a'val y = str2[j] - 'a'if ((y - x + U) % U <= 1) {if (++j == m) break}}return m == j}
}

复杂度分析：

时间复杂度： $O (n + m)$ i 指针和 j 指针最多移动 n + m 次；
空间复杂度： $O (1)$ 仅使用常量级别空间。

T3. 将三个组排序（Medium）

https://leetcode.cn/problems/sorting-three-groups/

题解一（状态机 DP）

根据题意，我们需要构造出非递减数组，并使得操作次数最小。

观察测试用例可以发现逆序数是问题的关键，如示例 1 [2,1,3,2,1] 中存在 2 → 1，3 → 2，2 → 1 的逆序对，且结果正好是 3。然而这个思路是错误的，我们可以构造特殊测试用例 [3,3,3,1,1,1] 来验证。

那应该怎么解呢？我们发现问题是可以划分为子问题的。定义 dp[i][j] 表示到 [i] 为止构造出以 j 为结尾的非递减数组的最少操作次数，那么 dp[i+1][j] 可以从 dp[i] 的三个子状态转移过来：

dp[i][1] 可以转移到 dp[i+1][1] 和 dp[i+1][2] 和 dp[i+1][3]
dp[i][2] 可以转移到 dp[i+1][2] 和 dp[i+1][3]
dp[i][3] 可以转移到 dp[i+1][3]

最后，求出 dp[n][1]、dp[n][2] 和 dp[n][3] 中的最小值即为问题的解。

class Solution {fun minimumOperations(nums: List<Int>): Int {val n = nums.sizeval U = 3val dp = Array(n + 1) { IntArray(U + 1) }for (i in 1 .. n) {for (j in 1 .. U) {dp[i][j] = dp[i - 1].slice(1..j).min()!!if (j != nums[i - 1]) dp[i][j] += 1}}return dp[n].slice(1..U).min()!!}
}

另外，dp[i+1] 只与 dp[i] 有关，我们可以使用滚动数组优化空间复杂度：

class Solution {fun minimumOperations(nums: List<Int>): Int {val n = nums.sizeval U = 3val dp = IntArray(U + 1)for (i in 0 until n) {for (j in U downTo 1) { // 逆序dp[j] = dp.slice(1..j).min()!!if (j != nums[i]) dp[j] += 1}}return dp.slice(1..U).min()!!}
}

复杂度分析：

时间复杂度： $O (C \cdot n)$ 仅需要线性时间，其中 $C$ = 9；
空间复杂度： $O (U)$ DP 数组空间， $U$ = 3。

题解二（LIS 问题）

这道题还有第二种思路，我们可以计算数组的最长非递减子序列长度 LIS，再使用原数组长度 n - 最长非递减子序列长度 LIS，就可以得出最少操作次数。

LIS 问题有两个写法：

写法 1 · 动态规划

class Solution {fun minimumOperations(nums: List<Int>): Int {val n = nums.size// dp[i] 表示以 [i] 为结尾的 LISval dp = IntArray(n) { 1 }var len = 1for (i in 0 until n) {for (j in 0 until i) {if (nums[i] >= nums[j]) dp[i] = Math.max(dp[i], dp[j] + 1)}len = Math.max(len, dp[i])}return n - len}
}

复杂度分析：

时间复杂度： $O(n^2)$ 内存循环的时间复杂度是 $O (n)$ ；
空间复杂度： $O (n)$ DP 数组空间。

写法 2 · 动态规划 + 贪心 + 二分查找

class Solution {fun minimumOperations(nums: List<Int>): Int {val n = nums.sizeval dp = IntArray(n + 1)var len = 1dp[len] = nums[0]for (i in 1 until n) {if (nums[i] >= dp[len]) {dp[++len] = nums[i]} else {// 二分查找维护增长更慢的序列：寻找大于 nums[i] 的第一个数var left = 1var right = lenwhile (left < right) {val mid = (left + right) ushr 1if (dp[mid] <= nums[i]) {left = mid + 1} else {right = mid }}dp[left] = nums[i]}}return n - len}
}

复杂度分析：

时间复杂度： $O (n l g n)$ 单次二分查找的时间复杂度是 $O (l g n)$ ；
空间复杂度： $O (n)$ DP 数组空间。

相似题目：

300. 最长递增子序列

T4. 范围中美丽整数的数目（Hard）

https://leetcode.cn/problems/number-of-beautiful-integers-in-the-range/

题解（数位 DP + 记忆化）

近期经常出现数位 DP 的题目。

1、数位 DP： 我们定义 dp[i, pre, diff, isNumber, isLimit] 表示从第 i 位开始的合法方案数，其中：
- pre 表示已经选择的数位前缀的值，当填入第 i 位的数字 choice 后更新为 pre * 10 + choice，在终止条件时判断 pre % k == 0；
- diff 表示已选择的数位中奇数和偶数的差值，奇数 + 1，而偶数 - 1，在终止条件时判断 diff == 0；
- isNumber 表示已填数位是否构造出合法数字；
- isLimit 表示当前数位是否被当前数位的最大值约束。
2、差值： 要计算出 [low, high] 之间的合法方案数，我们可以计算出 [0, high] 和 [0, low] 之间合法方案数的差值；
3、记忆化： 对于相同 dp[i, …] 子问题，可能会重复计算，可以使用记忆化优化时间复杂度：
4、特征压缩： 由于所有的备选数的 pre 都是不用的，这会导致永远不会命中备忘录，我们需要找到不同前缀的特征。
5、取模公式： 如果 $\% k == 0$ ，那么有 $\% k) * 10 + choice) \% k == 0$ ，我们可以提前对 pre 取模抽取出特征因子。

$\% mod == ((a \% mod) + (b \% mod)) \% mod$
$\% mod == ((a \% mod) · (b \% mod)) \% mod$

class Solution {private val U = 10fun numberOfBeautifulIntegers(low: Int, high: Int, k: Int): Int {return count(high, k) - count(low - 1, k)}private fun count(num: Int, k: Int): Int {// <i, diff, k>val memo = Array(U) { Array(U + U) { IntArray(k) { -1 }} }return f(memo, "$num", k, 0, 0, 0, true, false)}private fun f(memo: Array<Array<IntArray>>, str: String, k: Int, i: Int, mod: Int, diff: Int, isLimit: Boolean, isNumber: Boolean): Int {// 终止条件if (i == str.length) return if (0 != diff || mod % k != 0) 0 else 1// 读备忘录if (!isLimit && isNumber && -1 != memo[i][diff + U][mod]) {return memo[i][diff + U][mod] // 由于 diff 的取值是 [-10,10]，我们增加一个 U 的偏移}val upper = if (isLimit) str[i] - '0' else 9var ret = 0for (choice in 0 .. upper) {val newMod = (mod * 10 + choice) % k // 特征因子if (!isNumber && choice == 0) {ret += f(memo, str, k, i + 1, 0, 0, false, false)continue} if (choice % 2 == 0) {ret += f(memo, str, k, i + 1, newMod, diff + 1, isLimit && choice == upper, true)} else {ret += f(memo, str, k, i + 1, newMod, diff - 1, isLimit && choice == upper, true)}   }// 写备忘录if (!isLimit && isNumber) {memo[i][diff + U][mod] = ret}return ret}
}

复杂度分析：

时间复杂度： $O(C^2·k·D)$ 其中 $C$ 为最大数位长度 10， $D$ 为选择方案 10。状态数为 “i 的值域 * diff 的值域 * mod 的值域” = $C^2·k$ ，单个状态的时间复杂度是 $O (D)$ ，整体的时间复杂度是状态数 · 状态时间 = $O(C^2·k·D)$ ；
空间复杂度： $O(C^2·k)$ 备忘录空间。

相似题目：

2801. 统计范围内的步进数字数目

推荐阅读

LeetCode 上分之旅系列往期回顾：

LeetCode 单周赛第 358 场 · 结合中心扩展的单调栈贪心问题
LeetCode 单周赛第 357 场 · 多源 BFS 与连通性问题
LeetCode 双周赛第 110 场 · 结合排序不等式的动态规划
LeetCode 双周赛第 109 场 · 按部就班地解决动态规划问题