目录
中国剩余定理解释
中国剩余定理扩展——求解模数不互质情况下的线性方程组:
代码实现:
互质:
非互质:
中国剩余定理解释
在《孙子算经》中有这样一个问题:“今有物不知其数,三三数之剩二(除以3余2),五五数之剩三(除以5余3),七七数之剩二(除以7余2),问物几何?”这个问题称为“孙子问题”,该问题的一般解法国际上称为“中国剩余定理”。具体解法分三步:
-
- 找出三个数:从3和5的公倍数中找出被7除余1的最小数15,从3和7的公倍数中找出被5除余1 的最小数21,最后从5和7的公倍数中找出除3余1的最小数70。
- 用15乘以2(2为最终结果除以7的余数),用21乘以3(3为最终结果除以5的余数),同理,用70乘以2(2为最终结果除以3的余数),然后把三个乘积相加15∗2+21∗3+70∗2得到和233。
- 用233除以3,5,7三个数的最小公倍数105,得到余数23,即233%105=23。这个余数23就是符合条件的最小数。
就这么简单。我们在感叹神奇的同时不禁想知道古人是如何想到这个方法的,有什么基本的数学依据吗?
我们将“孙子问题”拆分成几个简单的小问题,从零开始,试图揣测古人是如何推导出这个解法的。
首先,我们假设n1是满足除以3余2的一个数,比如2,5,8等等,也就是满足3∗k+2(k>=0)的一个任意数。同样,我们假设n2是满足除以5余3的一个数,n3是满足除以7余2的一个数。
有了前面的假设,我们先从n1这个角度出发,已知n1满足除以3余2,能不能使得n1+n2的和仍然满足除以3余2?进而使得n1+n2+n3的和仍然满足除以3余2?
这就牵涉到一个最基本数学定理,如果有a%b=c,则有(a+k∗b)%b=c(k为非零整数),换句话说,如果一个除法运算的余数为c,那么被除数与kk倍的除数相加(或相减)的和(差)再与除数相除,余数不变。这个是很好证明的。
以此定理为依据,如果n2是3的倍数,n1+n2就依然满足除以3余2。同理,如果n3也是3的倍数,那么n1+n2+n3的和就满足除以3余2。这是从n1的角度考虑的,再从n2,n3的角度出发,我们可推导出以下三点:
-
- 为使n1+n2+n3的和满足除以3余2,n2和n3必须是3的倍数。
- 为使n1+n2+n3的和满足除以5余3,n1和n3必须是5的倍数。
- 为使n1+n2+n3的和满足除以7余2,n1和n2必须是7的倍数。
因此,为使n1+n2+n3的和作为“孙子问题”的一个最终解,需满足:
- n1除以3余2,且是5和7的公倍数。
- n2除以5余3,且是3和7的公倍数。
- n3除以7余2,且是3和5的公倍数。
所以,孙子问题解法的本质是从5和7的公倍数中找一个除以3余2的数n1,从3和7的公倍数中找一个除以5余3的数n2,从3和5的公倍数中找一个除以7余2的数n3,再将三个数相加得到解。在求n1,n2,n3时又用了一个小技巧,以n1为例,并非从5和7的公倍数中直接找一个除以3余2的数,而是先找一个除以3余1的数,再乘以2。也就是先求出5和7的公倍数模3下的逆元,再用逆元去乘余数。
这里又有一个数学公式,如果a%b=c,那么(a∗k)%b=a%b+a%b+…+a%b=c+c+…+c=k∗c(k>0),也就是说,如果一个除法的余数为c,那么被除数的k倍与除数相除的余数为k∗c。展开式中已证明。
最后,我们还要清楚一点,n1+n2+n3只是问题的一个解,并不是最小的解。如何得到最小解?我们只需要从中最大限度的减掉掉3,5,7的公倍数105即可。道理就是前面讲过的定理“如果a%b=ca%b=c,则有(a−k∗b)%b=c(a−k∗b)%b=c”。所以(n1+n2+n3)%105就是最终的最小解。
这样一来就得到了中国剩余定理的公式:
设正整数
两两互素,则同余方程组
有整数解。并且在模
下的解是唯一的,解为
其中
,而
为
模
的逆元。
中国剩余定理扩展——求解模数不互质情况下的线性方程组:
普通的中国剩余定理要求所有的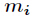
这种情况就采用两两合并的思想,假设要合并如下两个方程:
那么得到:
我们需要求出一个最小的xx使它满足:
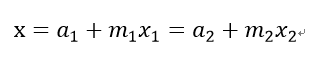
那么x1和x2就要尽可能的小,于是我们用扩展欧几里得算法求出x1的最小正整数解,将它代回a1+m1x1,得到xx的一个特解x′,当然也是最小正整数解。
所以xx的通解一定是x′加上lcm(m1,m2)∗klcm(m1,m2)∗k,这样才能保证x模m1和m2的余数是a1和a2。由此,我们把这个x′当做新的方程的余数,把lcm(m1,m2)当做新的方程的模数。(这一段是关键)
合并完成:
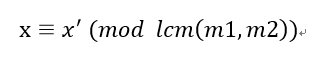
代码实现:
互质:
//求M%A=a,M%B=b,...中的M,其中A,B,C...互质
int CRT(int a[],int m[],int n){ int M = 1; int ans = 0; for(int i=1; i<=n; i++) M *= m[i]; for(int i=1; i<=n; i++){ int x, y; int Mi = M / m[i]; ex_gcd(Mi, m[i], x, y); ans = (ans + Mi * x * a[i]) % M; } if(ans < 0) ans += M; return ans;
} 非互质:
bool merge(LL a1, LL m1, LL a2, LL m2, LL &a3, LL &m3) { LL d = gcd(m1, m2); LL c = a2 - a1; if(c % d) return false; c = (c % m2 + m2) % m2; m1 /= d; m2 /= d; c /= d; c *= Inv(m1, m2);//Inv为乘法逆元,数论常用内容——欧几里得算法与扩展欧几里得算法c %= m2; c *= m1 * d; c += a1; m3 = m1 * m2 * d; a3 = (c % m3 + m3) % m3; return true;
} LL CRT(LL a[], LL m[], int n) { LL a1 = a[1]; LL m1 = m[1]; for(int i=2; i<=n; i++) { LL a2 = a[i]; LL m2 = m[i]; LL m3, a3; if(!merge(a1, m1, a2, m2, a3, m3)) return -1; a1 = a3; m1 = m3; } return (a1 % m1 + m1) % m1;
} 参考:数论常用内容——中国剩余定理
下一篇:Codeforces Round 153 (Rated for Div. 2)
推荐音乐:沉沦于遐想


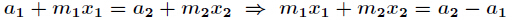







![java八股文面试[java基础]——String StringBuilder StringBuffer](https://img-blog.csdnimg.cn/84d235ec45c4452897adb62867caeaeb.png)