摘要
脉冲相机使用了“integrate and fire”机制来生成连续的脉冲流,以极高的时间分辨率来记录动态光照强度。但是极高的时间分辨率导致了受限的空间分辨率,致使重建出的图像无法很好保留原始场景的细节。为了解决这个问题,这篇文章提出了SpikeSR-Net来从低分辨率二进制脉冲流中恢复出高像素图像。Spike-Net基于脉冲相机模型进行设计,融合和基于模型和学习的方法。为了解决二进制数据有限的表达能力,文中提出了一个像素自适应的脉冲编码器,将脉冲转化为潜在的表达,用以推测光照强度以及物体的运动信息。然后,一个运动对其的超分辨率器被用来探索长期关联,从而时间域的密集采样(对应其超高的时间分辨率)可以被用来增强其空间分辨率,并且不引入运动模糊。实验结果显示SpikeSR-Net取得了很好的结果。
介绍
新兴的实时计算机视觉应用,比如自动驾驶,无人机技术等都需要机器能够清楚地记录高速运动并且迅速响应。这暴露了传统相机的不足。传统的相机主要是基于一次性曝光成像,对静态场景或者低速运动可以进行很好的成像。但是对于高度运动,运动物体上的某一点可能会被投影到传感器的不同像素上,导致运动模糊。
为了清晰地捕捉高动态场景,脉冲相机被发明。不同于传统相机将所有一个曝光周期内的所有视觉信息压缩成一张快照,脉冲相机没有采用曝光窗口的概念。相反,脉冲相机持续连续地监控到达的光线,然后输出二进制脉冲流来记录极高时间分辨率下的动态场景(40000hz)。除此之外,不同于使用微分采样模型记录光照变化的事件相机,脉冲相机发出脉冲,当到达的光子数量达到所设阈值时。这种集成的采样模式使得脉冲相机可以记录每个像素点的亮度强度,给恢复纹理信息提供更多明显的信息。
对于脉冲相机来说,图像重建是弥补二值脉冲和光强之间域差异的重要手段。这在过去几年中吸引了很多的注意力。然后,之前的工作由于以下的问题,常常会出现噪声、运动模糊和不满意的细节:
(1)超高速运动。由于超高速运动,一个传感器像素发出的脉冲不在描述运动物体上的同一点了。因此,需要特别注意避免来自不同物体点的灯光的混合。
(2)不理想的噪声。由于光子到达的泊松效应和热噪声的存在,临近脉冲的发射间隔存在剧烈的波动。因为这个原因,重建结果噪声较多,不稳定并且存在时空不一致的问题。
(3)有限的空间分辨率。作为对高时间分辨率的权衡,脉冲相机的空间分辨率首先,导致了重建细节不佳。
为了解决上述问题,本文提出了一个端到端的脉冲相机超分辨率网络SpikeSR-Net,旨在对脉冲流进行超分辨率处理,得到高像素的强度图像。具体来说,我们首先提出了像素自适应脉冲编码器(PASE, pixel-adaptive spike encoder)来将原始的二进制脉冲转化为潜在的强度表达。考虑到场景内容的多样性,PASE自适应地探索局部时空关联来解决不同的运动和光照条件。然后,我们提出了运动对齐超分辨率器(MASR, motion-aligned super resolver),用来循环进行运动对齐的梯度下降和近端映射。MASR运用长期时间联合将时域的密集采样转化到空间域中,使得超分辨率化后的图像拥有了更加细致的细节,高的最大信噪比(PSNR)和更少的模糊。在真实以及合成脉冲数据上的实验结果显示了Spike-Net优越的性能。
这项工作的主要贡献如下:
(1)我们设计了一个基于优化的网络,通过结合基于模型以及基于学习方法的优点来超像素化二进制脉冲数据流,获得拥有更高质量纹理细节的强度图像。
(2)我们提出了像素自适应的脉冲编码器来将二进制的脉冲传化为潜在的表达。编码器自适应地探索时空一致性来解决不同的运动和光照情况。所提出的方法还可以被灵活地运用到其他脉冲相机任务中。
(3)我们设计了一个展开的运动对齐超像素器,通过循环运用梯度下降以及近端映射,使得网络可以探索长期的时空关系来提升图像的信噪比以及纹理细节。
问题描述
脉冲相机的基础
脉冲相机使用了“integrate-and-fire”机制来连续地对到达的光照 I ( t ) I(t) I(t)进行累计。当到达阈值 θ \theta θ时,一个脉冲会被激发并且积分器归零。假设 t 1 , t 2 , . . . , t n {t_1, t_2,...,t_n} t1,t2,...,tn是生成的脉冲的发射时间,第 k k k个脉冲的产生过程可以描述为:
∫ t k − 1 t k η I ( x ) d x = θ (1) \int_{t_{k-1}}^{t_k}\eta I(x)dx=\theta \tag{1} ∫tk−1tkηI(x)dx=θ(1)
其中 η \eta η表示光电转化率。脉冲图像传感器上的一个像素可能在任意时间发射脉冲,但是相机只能以离散二进制的形式读出脉冲信号 S ( n ) S(n) S(n)。具体说来,在 t k t_k tk时间激发的第 k k k个脉冲会被读出并表示为 S ( n k ) = 1 S(n_k)=1 S(nk)=1,其中 η k = ⌈ t k / δ ⌉ \eta_k=\lceil t_k/\delta \rceil ηk=⌈tk/δ⌉, δ \delta δ是脉冲相机的读出间隔。
脉冲相机超像素成像
如图一所示,由于相机和物体之间的相对运动,脉冲相机在不同的时刻可能是在不同的位置进行采样的。进一步说来,脉冲相机用极高的时间分辨率记录了动态场景,进而产生了亚像素位移,并且为超像素提供了亚像素覆盖。
假设 X k X_k Xk表示 k k k时刻的高分辨率(HD)图像。基于光度一致性假设,脉冲相机高分辨率成像的观测模型可以表示为:
Y i = D s H i T k → i X k + N i , i = 1 , 2 , . . . , n S 1 , S 2 , . . . , S n = T ( { Y 1 , Y 2 , Y 3 } , θ ) (2) Y_i=\mathcal{D}_s\mathcal{H}_i\mathcal{T}_{k\rightarrow i}X_k+N_i, \ i=1,2,...,n\\\\ {S_1,S_2,...,S_n}=T(\{Y_1,Y_2,Y_3\},\theta)\tag{2} Yi=DsHiTk→iXk+Ni, i=1,2,...,nS1,S2,...,Sn=T({Y1,Y2,Y3},θ)(2)
这里 H i \mathcal{H_i} Hi和 T k → i \mathcal{T}_{k\rightarrow i} Tk→i分别代表模糊退化以及运动变换矩阵。 D s \mathcal{D}_s Ds表示以 s s s为缩放系数进行的下采样。 N i N_i Ni是额外的噪声。 { Y 1 , Y 2 , . . . , Y n } \{Y_1,Y_2,...,Y_n\} {Y1,Y2,...,Yn}是不同时刻退化后的低分辨率强度信息。 T ( ⋅ ) T(\cdot) T(⋅)表示脉冲相机的“integrate-and-fire”机制,进而产生二进制的脉冲流。脉冲相机超分辨率(SCSR, spike camera super resolution)的目的是将时域中的密集采样转化到空间域中,超分辨率化低像素的脉冲数据 { S 1 , S 2 , S 3 } \{S_1,S_2,S_3\} {S1,S2,S3}来获得高质量的高分辨率强度图像 X ^ k \hat{X}_k X^k。

方法
整体流程
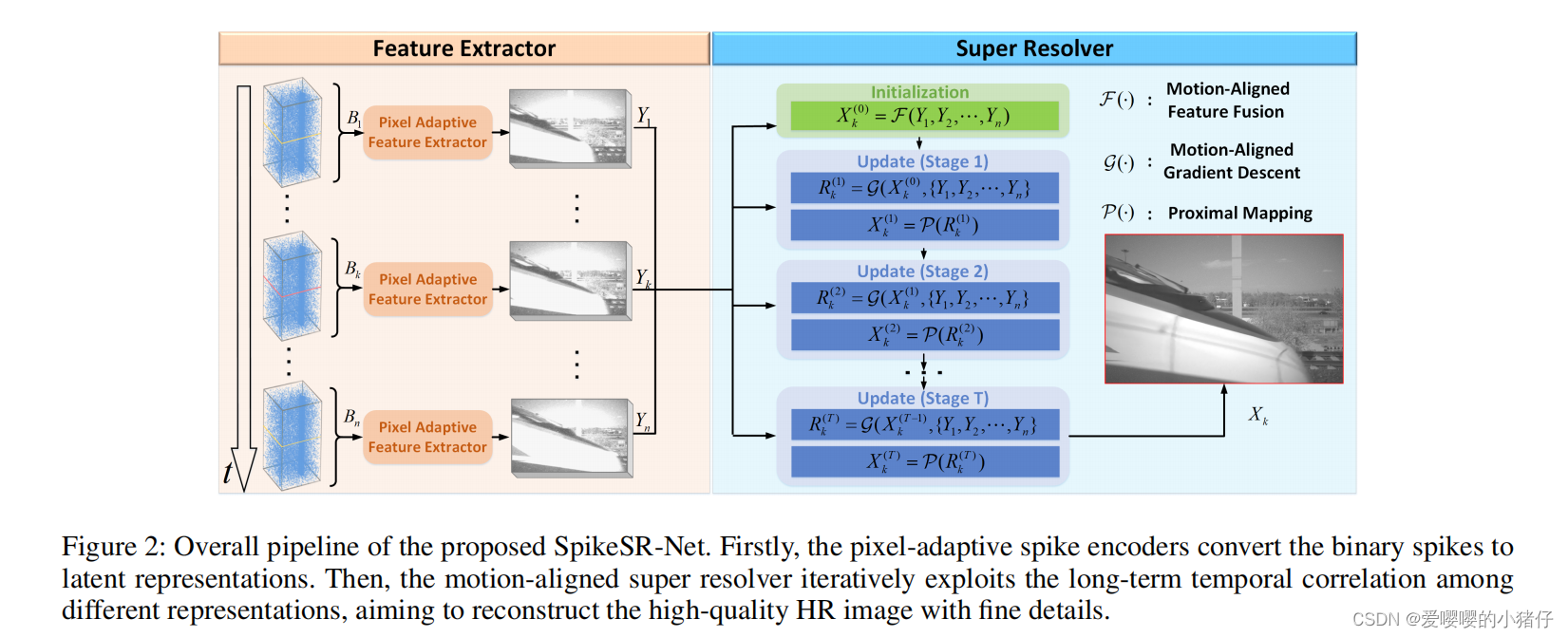
收到SCSR观测模型的启发,本文提出了一个端到端可训的SCSR模型,称为Spike-Net来从低分辨率的脉冲流中得到超分辨率化的图像。图二展示了Spike-Net的整体流程。它将第 k k k帧附近连续的脉冲帧 { S k + 1 } , i = ± 1 , ± 2 , . . . \{S_{k+1}\},i=\pm1,\pm2,... {Sk+1},i=±1,±2,...作为输入,使得网络可以探索空间关联来生成高质量的高像素图像 X ^ k \hat{X}_k X^k。网络主要包含两部分,PASE和MASR。首先,输入的脉冲流会被分成一些重叠的短期的脉冲块 { B i } , i ∈ { 1 , 2 , . . . , k , . . . , n − 1 , n } \{B_i\},i\in\{1,2,...,k,...,n-1,n\} {Bi},i∈{1,2,...,k,...,n−1,n}。PASE E \mathcal{E} E自适应地探索每一个二进制脉冲块之间的时空关联,产生潜在的强度表示 { Y i } \{Y_i\} {Yi}:
Y i = E ( B i ) (3) Y_i=\mathcal{E}(B_i)\tag{3} Yi=E(Bi)(3)
然后,超分辨率器的目标可以描述为:
arg min X k ∑ i = 1 n w i ⋅ ∣ ∣ D s H i T k → i X k − Y i ∣ ∣ 2 2 + λ Ψ ( X k ) (4) \arg \mathop{\min}\limits_{X_k}\sum_{i=1}^nw_i\cdot||\mathcal{D}_s\mathcal{H}_i\mathcal{T}_{k\rightarrow i}X_k-Y_i||_2^2+\lambda\Psi(X_k)\tag{4} argXkmini=1∑nwi⋅∣∣DsHiTk→iXk−Yi∣∣22+λΨ(Xk)(4)
其中, w i w_i wi表示关于噪声 N i N_i Ni的权重。 Ψ ( X k ) \Psi(X_k) Ψ(Xk)表示高像素图像的先验, λ \lambda λ表示正则项。上述的逆问题可以通过迭代下面的更新步骤进行解决:
R k ( t ) = X k t − 1 − β ∑ i = 1 n w i T k → i T H i T D s T ( D s H i T k → i X k t − 1 − Y i ) X k ( t ) = arg min X k ∣ ∣ X k − R k ( t ) ∣ ∣ 2 2 + λ Ψ ( X k ) (5) R_k^{(t)}=X_k^{t-1}-\beta\sum_{i=1}^nw_i\mathcal{T}_{k\rightarrow i}^T\mathcal{H}_i^T\mathcal{D}_s^T(\mathcal{D}_s\mathcal{H}_i\mathcal{T}_{k\rightarrow i}X_k^{t-1}-Y_i)\\\\ X_k^{(t)}=\arg \mathop{\min}\limits_{X_k}||X_k-R_k^{(t)}||_2^2+\lambda\Psi(X_k)\tag{5} Rk(t)=Xkt−1−βi=1∑nwiTk→iTHiTDsT(DsHiTk→iXkt−1−Yi)Xk(t)=argXkmin∣∣Xk−Rk(t)∣∣22+λΨ(Xk)(5)
这里 β \beta β是更新率。(这里面用到了ADMM算法)
受到优化过程过程的启发,我们设计了一个迭代的基于CNN的超分辨率器来进一步探索长期的时间关联并且构建更加细致的高分辨率图像。具体的流程可以表示为:
R k ( t ) = G ( X k ( t − 1 ) , Y 0 , Y 1 , . . . , Y n ) X k ( t ) = P ( R k ( t ) ) (6) R_k^{(t)}=\mathcal{G}(X_k^{(t-1)},{Y_0,Y_1,...,Y_n})\\\\ X_k^{(t)}=\mathcal{P}(R_k^{(t)})\tag{6} Rk(t)=G(Xk(t−1),Y0,Y1,...,Yn)Xk(t)=P(Rk(t))(6)
G ( ⋅ ) \mathcal{G}(\cdot) G(⋅)和 P ( ⋅ ) \mathcal{P}(\cdot) P(⋅)分别代表梯度下降模块(GDM, gradient decent module)和近端映射模块(PMM, proximal mapping module)。 E ( ⋅ ) \mathcal{E}(\cdot) E(⋅), G ( ⋅ ) \mathcal{G}(\cdot) G(⋅)和 P ( ⋅ ) \mathcal{P}(\cdot) P(⋅)的细节会在接下来的部分详细讨论。
PASE
在脉冲相机中,每一个脉冲的激发表示着到达了一定的光子,这个积累的过程可能会延续好几个读出周期。也就是说,除了代表实时性的强度信息,每一个脉冲还暗含了有限的视觉信息。为了解决这一问题,我们设计了PASE来将二进制脉冲流转化成潜在的强度表达。
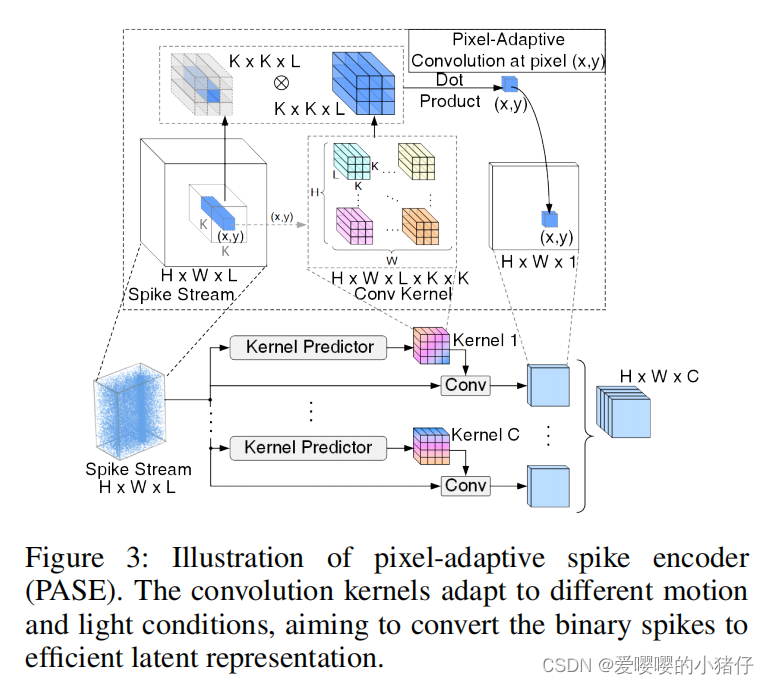
图三展示了所提出的PASE。为了增强表达能力,卷积被用来探索脉冲流之间的局部时空关联。然而,场景内容的多样性可能会导致关联结构的多样性,而固定的卷积kernel难以很好地处理多种内容。举例来说,对于高速运动或者有高频率边的区域,注意力应该放在避免模糊上。因此,相比于直接使用固定的卷积网络提取特征,PASE使用卷积网络来分析脉冲块 B i B_i Bi之间的关联结构,并且生成一组可学习的kernel特征 K i H × W × L K 2 \mathcal{K}_i^{H\times W\times LK^2} KiH×W×LK2。其中 H H H, W W W和 L L L是输入脉冲块的高度、宽度和长度。 K K K是滤波器的尺寸。然后,kernel特征会被重塑为 H × W H\times W H×W的线性滤波器 K i , j ′ K × K × L K_{i,j}^{'K\times K\times L} Ki,j′K×K×L,并且每个滤波器都被用来为相应的输入块提取瞬时的强度信息:
Y i ( x , y ) = K i , j ′ ( x , y ) ⊗ P i ( x , y ) (7) Y_i(x,y)=K'_{i,j}(x,y)\otimes P_i(x,y)\tag{7} Yi(x,y)=Ki,j′(x,y)⊗Pi(x,y)(7)
其中, K i , j ′ ( x , y ) K'_{i,j}(x,y) Ki,j′(x,y)表示 P i ( x , y ) P_i(x,y) Pi(x,y)对应的第 j j j个kernel, P i ( x , y ) P_i(x,y) Pi(x,y)表示以 ( x , y ) (x,y) (x,y)为中心的 K × K × L K \times K \times L K×K×L的二进制脉冲块。除此之外,为了增强PASE的能力。我们使用一些平行的分支来生成多组kernel。不同组的滤波器尺寸可以是不同的,所以PASE可以拥有不同的感受野。PASE的输出是一系列从不同分支中获得的特征,可以表示为 Y i = [ Y i 1 , Y i 2 , . . . , Y i C ] Y_i=[Y_i^1,Y_i^2,...,Y_i^C] Yi=[Yi1,Yi2,...,YiC]。其中 C C C是分支数。在本文中,PASE被用在所有的短期脉冲块中,生成了一系列的潜在表达 Y 1 , Y 2 , Y 3 {Y_1,Y_2,Y_3} Y1,Y2,Y3。
MASR
超分辨率器的目标是重建高分辨,拥有更多细节的强度图像。为此,我们进一步探索了不同时刻之间的长期时间关联,从而将时域上的密集采样转化到空间域上。考虑到室外场景中的高速运动,我们格外在意对运动的避免。收到优化模型的启发,我们提出了基于运动对齐的GDM G ( ⋅ ) \mathcal{G(\cdot)} G(⋅)和PMM P ( ⋅ ) \mathcal{P(\cdot)} P(⋅)来发挥长期关联的优势并且迭代优化细节。
基于运动对齐的GDM
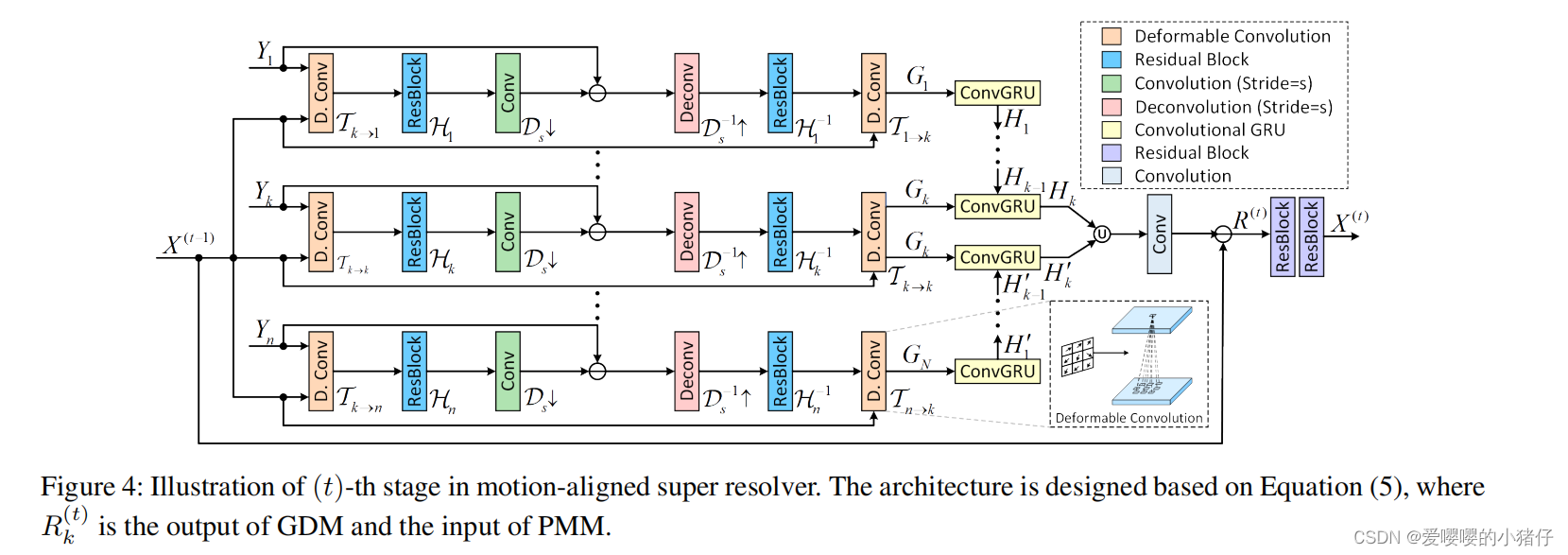
图四展示了基于运动对齐的GDM G ( ⋅ ) \mathcal{G(\cdot)} G(⋅)的架构。根据公式(5),我们采用梯度计算单元,基于不同时刻的潜在表示来计算梯度。第 i i i个分支的梯度计算单元可以被定义为:
对齐: E i ( t ) = T k → i ( [ X k ( t − 1 ) , D s − 1 ( Y i ) ] ) (8) E_i^{(t)}=\mathcal{T}_{k\rightarrow i}([X_k^{(t-1)},\mathcal{D}_s^{-1}(Y_i)])\tag{8} Ei(t)=Tk→i([Xk(t−1),Ds−1(Yi)])(8)
按比例缩减: L i ( t ) = D s ( H i ( E i ( t ) ) ) (9) L_i^{(t)}=\mathcal{D}_s(\mathcal{H}_i(E_i^{(t)}))\tag{9} Li(t)=Ds(Hi(Ei(t)))(9)
缩放残余: F i ( t ) = H s − 1 ( D i − 1 ( L i ( t ) − Y i ) ) (10) F_i^{(t)}=\mathcal{H}_s^{-1}(\mathcal{D}_i^{-1}(L_i^{(t)}-Y_i))\tag{10} Fi(t)=Hs−1(Di−1(Li(t)−Yi))(10)
对齐: G i ( t ) = T k → i − 1 ( [ F i ( t ) , X k ( t − 1 ) ] ) (11) G_i^{(t)}=\mathcal{T}_{k\rightarrow i}^{-1}([F_i^{(t)},X_k^{(t-1)}])\tag{11} Gi(t)=Tk→i−1([Fi(t),Xk(t−1)])(11)
其中 [ , ] [,] [,]表示拼接。 D s ( ⋅ ) \mathcal{D}_s(\cdot) Ds(⋅)和 D s − 1 ( ⋅ ) \mathcal{D}_s^{-1}(\cdot) Ds−1(⋅)是基于卷积和反卷积(stride为 s s s)的下采样和上采样操作。 H i ( ⋅ ) \mathcal{H}_i(\cdot) Hi(⋅)和 H i − 1 ( ⋅ ) \mathcal{H}_i^{-1}(\cdot) Hi−1(⋅)是基于残差块的退化和精修操作。 T k → i ( ⋅ ) \mathcal{T}_{k\rightarrow i}(\cdot) Tk→i(⋅)表示可变形卷积,它可以对齐 k k k时刻的特征以及 i i i时刻的特征,并且有 T k → i − 1 ( ⋅ ) = T i → k ( ⋅ ) \mathcal{T}_{k\rightarrow i}^{-1}(\cdot)=\mathcal{T}_{i\rightarrow k}(\cdot) Tk→i−1(⋅)=Ti→k(⋅)。在可变性卷积中,额外的偏置会被习得来增强空间采样位置,这在低层的计算机视觉领域展示了强大的转化模型能力。这里,我们使用可变性卷积来对齐不同时刻的特征,以避免运动模糊。
接下来,为了进一步探索长期时间关联,我们引入了基于ConvGRU的双向特征融合来自适应地整合梯度 { G 1 ( t ) , G 2 ( t ) , . . . , G n ( t ) } \{G_1^{(t)},G_2^{(t)},...,G_n^{(t)}\} {G1(t),G2(t),...,Gn(t)}。每一个ConvGRU包含了一个可学习的更新门和一个可学习的置位门。前向整合过程可以描述为:
Q i ( t ) = tanh ( C o n v ( [ C i ( t ) ⊙ H i − 1 , G i ( t ) ] ) ) H i ( t ) = ( 1 − Z i ( t ) ) ⊙ H i − 1 ( t ) + Z i ( t ) ⋅ Q i ( t ) (12) Q_i^{(t)}=\tanh(Conv([C_i^{(t)}\odot H_{i-1},G_i^{(t)}]))\\\\ H_i^{(t)}=(1-Z_i^{(t)})\odot H_{i-1}^{(t)}+Z_i^{(t)}\cdot Q_i^{(t)}\tag{12} Qi(t)=tanh(Conv([Ci(t)⊙Hi−1,Gi(t)]))Hi(t)=(1−Zi(t))⊙Hi−1(t)+Zi(t)⋅Qi(t)(12)
更新门 Z i ( t ) Z_i^{(t)} Zi(t)控制了多少现有的信息会被整合到新状态下。置位门 C i ( t ) C_i^{(t)} Ci(t)控制了多少之前额状态会被保留。 Z i ( t ) Z_i^{(t)} Zi(t)和 C i ( t ) C_i^{(t)} Ci(t)是基于 H i − 1 ( t ) H_{i-1}^{(t)} Hi−1(t)和 G i ( t ) G_i^{(t)} Gi(t)通过卷积和sigmoid激活操作得到的(所以这个 H i H_i Hi是怎么得到呢,看图四是 G i G_i Gi通过ConvGRU后得到的)。反向整合的和前向整合类似。GDM在 t t t时候的输出可以表示为:
R k ( t ) = X k ( t − 1 ) − C o n v ( [ H K ( t ) , H K ′ ( t ) ] ) (13) R_k^{(t)}=X_k^{(t-1)}-Conv([H_K^{(t)},H_K^{'(t)}])\tag{13} Rk(t)=Xk(t−1)−Conv([HK(t),HK′(t)])(13)
其中 H K ( t ) H_K^{(t)} HK(t)和 H K ′ ( t ) H_K^{'(t)} HK′(t)分别表示前向和后向的梯度整合。
前端映射模块(PMM)
紧接着,一个PMM P ( ⋅ ) \mathcal{P(\cdot)} P(⋅)被提出用来解决公式(5)中的前端映射问题。PMM的目标是修复 R k ( t ) R_k^{(t)} Rk(t)使其更接近理想的信号。为此,我们采用连接的残差块来优化细节,生成输出 X k t = P ( R k ( t ) ) X_k^{t}=\mathcal{P}(R_k^{(t)}) Xkt=P(Rk(t))。
因此,最终的重建可以表示为 X ^ k = X k ( T ) \hat{X}_k=X_k^{(T)} X^k=Xk(T),这里 T T T表示状态号(stage number,对应之前的不同分支么?)。
初始化
在开始循环之前,需要对 X k ( 0 ) X_k^{(0)} Xk(0)进行初始化。本文中,我们使用了一个基于运动对齐的混合模块 F ( ⋅ ) \mathcal{F}(\cdot) F(⋅)来初始化 X k ( 0 ) X_k^{(0)} Xk(0)。具体来说,我们首先使用可变性卷积,以 Y k Y_k Yk为准来对齐每一个临近的表达 Y i Y_i Yi。然后,我们使用基于双向ConvGRU的特征融合(如上所述)来整合对齐后的特征。最后,我们对整合的特征进行了上采样,并推导出 X k ( 0 ) X_k^{(0)} Xk(0)。
实现
数据准备
为了训练和评估SpikeSR-Net,需要脉冲数据集,包括低分辨率脉冲流和相应的高分辨率(HR)图像。然而,捕捉高质量的HR图像具有挑战性,特别是在高运动的动态场景中。为了解决这一问题,我们修改了(SpK2ImgNet)中的脉冲摄像机模拟器,以同时生成LR脉冲流和HR真值。本文考虑了基于图像的合成和基于视频的合成这两种模式。对于基于图像的合成,我们将每个被选择的图像视为要记录的场景,并假设在场景和传感器之间存在一个全局运动。我们使用来自DIV2K数据集的图像,来自REDS数据集和×4K1000FPS数据集的视频作为虚拟场景。训练数据集由600个脉冲流组成,这些脉冲流流是基于所有三个数据集生成的,以增强多样性。对于测试数据集,我们建立了一个基于DIV2K数据集的脉冲数据集和一个基于REDS数据集的脉冲数据集。每个测试数据集由40个脉冲序列组成。请注意,测试数据集和训练数据集之间没有重叠。
训练细节
在我们的实现中,在kernel预测器中使用了四个残差块。超分辨率器的级数设置为4。损失函数定义为:
L = λ t ∑ t = 1 T ∣ ∣ X k ( t ) − I k ∣ ∣ \mathcal{L}=\lambda_t\sum_{t=1}^T||X_k^{(t)}-I_k|| L=λtt=1∑T∣∣Xk(t)−Ik∣∣
其中 I k I_k Ik是 k k k时刻的真值。当 t < T t < T t<T时, λ t \lambda_t λt被设置为 0.1 0.1 0.1。否则, λ t \lambda_t λt将被设置为 1 1 1。我们将脉冲帧裁剪成40×40的patch,并将batch size设置为 6 6 6。在训练过程中,通过随机旋转 90 ° 、 180 ° 、 270 ° 90°、180°、270° 90°、180°、270°和水平翻转来进行数据增强。我们使用 A d a m Adam Adam优化器,并使用两个 G T X 1080 T i GTX 1080Ti GTX1080Ti GPU(PyTorch)实现我们的实验。该模型被训练了 30 30 30个epoch。
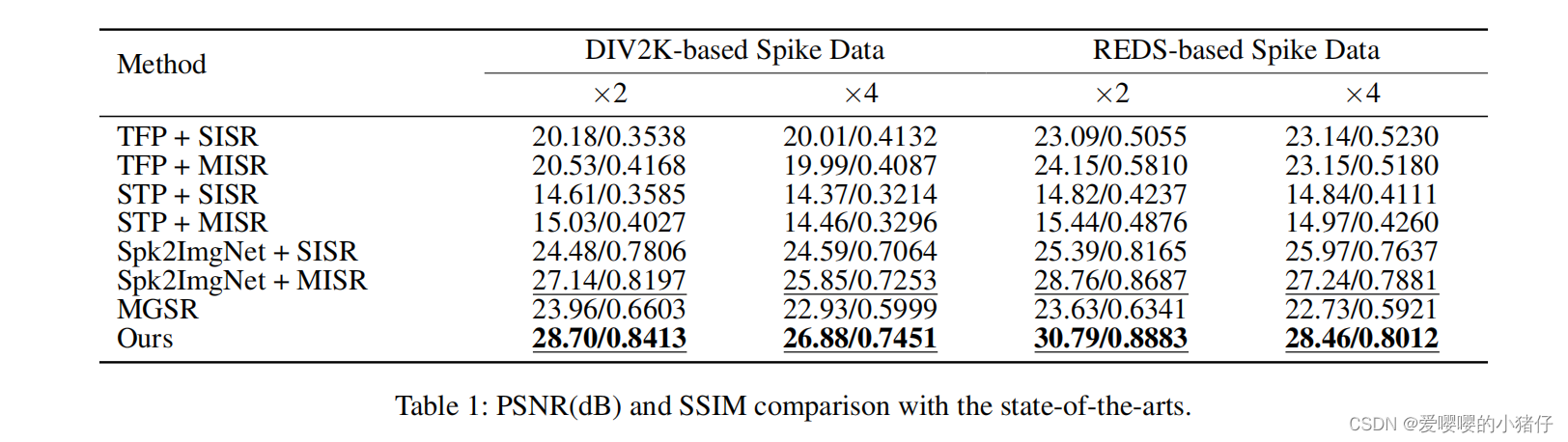
实验结果






![java八股文面试[java基础]——String StringBuilder StringBuffer](https://img-blog.csdnimg.cn/84d235ec45c4452897adb62867caeaeb.png)