在Android开发中通常我们使用flavor进行多渠道打包,flutter开发中同样有这种方式,不过需要在原生中配置
具体方案其实flutter官网个了相关示例(https://docs.flutter.dev/deployment/flavors),我这里记录一下自己的操作
Android
如下图,这里是android的

iOS
- 先创建一个新的Scheme

2.找到Configuration进行相关设置

3.根据不同的flavor可以设置不同的bundleId和产品名称

4.另外根据不同的flavor还可以进行设置咱们的开发环境,比如debug,test,release

5.在ios原生端自定义flavor字段

然后进行相关渠道的设置

这样就可以根据统一的渠道进行在flutter端开发相关代码
flutter根据flavor进行开发
 android端原生代码
android端原生代码

ios端原生代码

项目运行执行命令可用
flutter run --flavor freetest
另外
如果开发工具是vscode可以进行相关配置
穿件.vscode目录
然后创建launch.json文件。里面添加如下配置
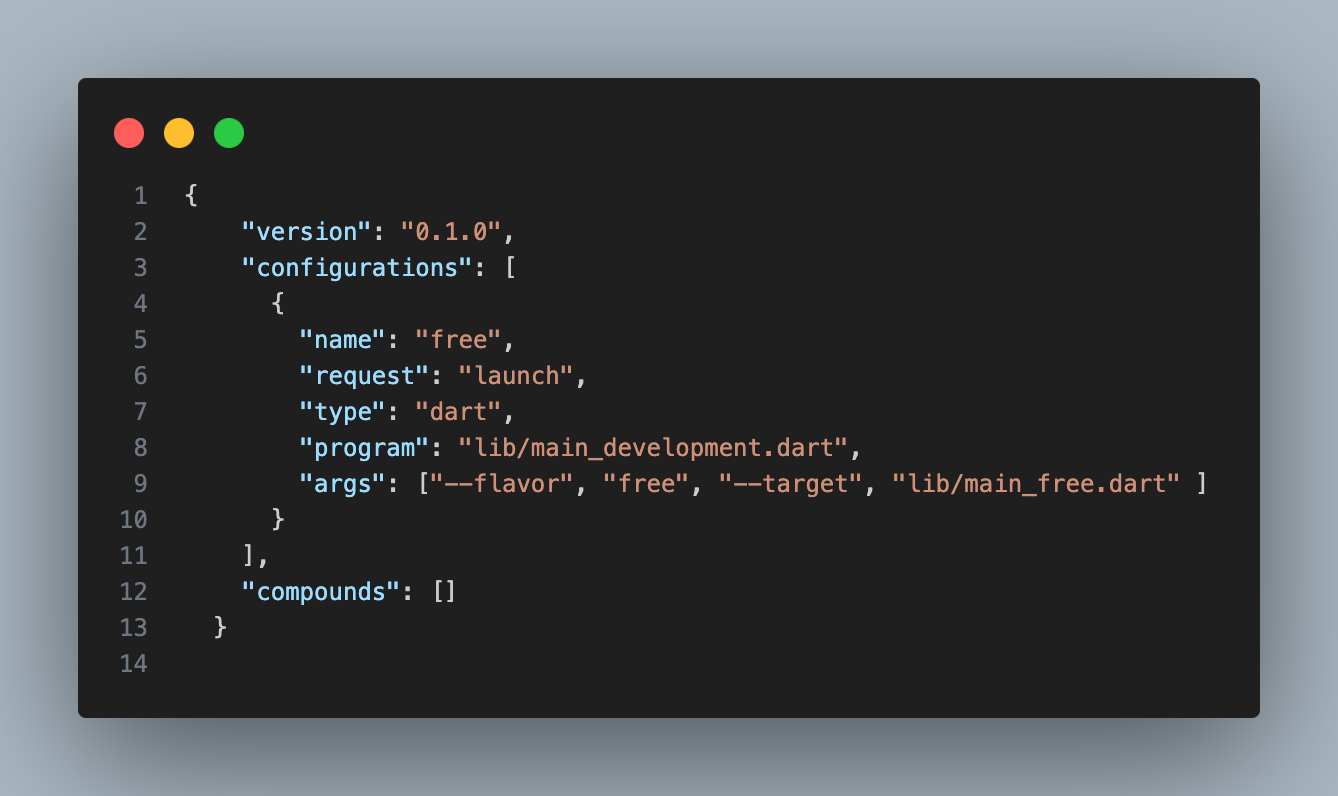
有了以上代码可以根据不同的flavor进行设置不同的代码,还可以多渠道打包
记录到此_



















